
2 Оцінка похибок вимірювання
2.1 Оцінка граничних значень основної та додаткової похибок
Проведено вимірювання за допомогою вольтметра з Uk, клас точності c/d отримано показ U В. Вимірювання здійснено при температурі навколишнього середовища Θ, магнітному полі напруженістю H=300 А/м, напруга живлення приладу Uж В. Температурна похибка не перевищує основну на кожних 100 С відхилення температури від нормальної області (20±2)0 С, магнітна – половини від основної при напруженості зовнішнього поля до 400 А/м, при відхиленні напруги живлення за межі 220 В ± 4% до значень від 187 до 240 В додаткова похибка не перевищує половини основної. Записати результат вимірювання. Значення Uk; c/d; U; Θ; Uж дивись табл.1 відповідно до варіанта.
Таблиця 1. Дані до завдання 1:
|
Варіант |
Uk, В |
c/d |
U |
Θ |
Uж |
|
9 |
200 |
0,1/0,02 |
100,1 |
5 |
202 |
Розв’язання
Похибка вимірювання складається з основної інструментальної, яка визначається за класом точності вольтметра та додаткових, зумовлених відхиленням температури навколишнього середовища від нормальної, наявність зовнішнього магнітного поля та відхилення напруги живлення поза межі допустимих значень.
1. Оскільки клас точності приладу нормовано сталими с та d, а саме 0,1/0,02, то основна відносна гранична похибка вимірювання напруги:

2.
Нормальний діапазон температури
навколишнього середовища від 18 до 22 ,
то ж значення температури навколишнього
середовища
,
то ж значення температури навколишнього
середовища відхиляється від нижньої зазначеної
межі на
відхиляється від нижньої зазначеної
межі на .
Тому зумовлена цим відносна гранична
похибка:
.
Тому зумовлена цим відносна гранична
похибка:

3. Напруженість зовнішнього магнітного поля Н=400 А/м, тому додаткова відносна гранична похибка зумовлена цим фактором:

4. Діапазон гранично допустимих значень напруги живлення:

Оскільки напруга живлення приладу становить 202 В, що є менше менше від нижньої межі, але входить в діапазон 187–240В, то зумовлена цим відносна гранична похибка:
 .
.
5. Тобто сумарна відносна гранична похибка вимірювання напруги:

6. Абсолютна гранична похибка вимірювання напруги:

Запишемо результат вимірювання напруги враховуючи, що похибку досить заокруглити до однієї або двох значущих цифр і кількість знаків після коми в написанні результату повинна відповідати кількості цих знаків у похибці. Тобто:
 .
.
2.2 Виведення виразів абсолютної та відносної похибок опосередкованого
вимірювання величини
Вивести вирази абсолютної та відносної похибок опосередкованого вимірювання величини y=f(X1,X2,X3).
Записати вирази похибок при заданих значення Х1,Х2,Х3 (дивись табл.2) відповідно до варіанта.
Таблиця 2. Дані до завдання 2:
|
Варіант |
Y(X1,X2,X3) |
X1 |
X2 |
X3 |
|
9 |
|
7,2 |
1,9 |
2,4 |
Розв’язання
Абсолютну похибку опосередкованого вимірювання можна визначити через повний диференціал виразу цього вимірювання. А саме:
 .
.
Тут:
 ;
;
 ;
; .
.

 .
.
Відносна похибка (у відносних одиницях):
 .
.
При
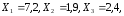 знайдемо:
знайдемо:

2.3 Отримання результатів спостережень при прямих рівно точних вимірюваннях
Для отриманих 12 результатів спостережень при прямих рівно точних вимірюваннях визначити оцінку результату вимірювань; оцінку дисперсії та СКВ випадкових похибок окремих результатів; оцінку СКВ результату вимірювання. Оцінити довірчі границі похибки для Рдов. Записати результат. Ряд спостережень та значення Рдов див. табл.3 відповідно до варіанта.
Таблиця 3. Дані до завдання 3:
|
Варіант |
данні |
Рдов | ||||||||||||
|
9 |
23,11 |
23,09 |
23,10 |
23,11 |
23,19 |
23,14 |
23,01 |
23,07 |
23,19 |
23,06 |
23,13 |
23,17 |
0,95 | |
Розв’язання
Найкращою оцінкою багатократних прямих рівно точних вимірювань, що дає змогу зменшити вплив випадкових складових похибки вимірювання кожного окремого спостереження, є середнє значення:
 .
.
Незміщена оцінка дисперсії сукупності спостережених значень:

Проаналізуємо чи немає серед спостережень грубих (аномальних) помилок. Сформуємо із спостережень варіаційний ряд (від найменшого значення до найбільшого)
23,01; 23,06; 23,07; 23,09; 23,10; 23,11; 23,11; 23,13; 23,14; 23,17; 23,19; 23,19.
Перевіримо крайні члени ряду на аномальність. Знайдемо співвідношення:


За
табл.1 (додаток), що задає допустимі
значення про нормованих відхилень від
середнього і заданою довірчою ймовірністю,
знайдемо
 ,
а саме: для
,
а саме: для ,
а отже, надійності
,
а отже, надійності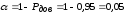 ,
та n=12 маємо
,
та n=12 маємо .
Оскільки
.
Оскільки та
та менші від
менші від ,
то кратні значення (варіанти) варіаційного
ряду не треба розглядати, як аномальні.
Незміщена оцінка середньоквадратичного
відхилення середнього значення:
,
то кратні значення (варіанти) варіаційного
ряду не треба розглядати, як аномальні.
Незміщена оцінка середньоквадратичного
відхилення середнього значення:

Оскільки
кількість спостережень
 <
30, то при оцінюванні гарантійного
(довірчого) інтервалу для похибки
середнього доцільно скористатися не
розподілом Гауса, а Стьюдента. За табл..
2 (додаток), що задає допустимі значення
гарантійного коефіцієнта для заданої
гарантійної (довірчої) ймовірності,
знайдемо відповідний коефіцієнт. А саме
для n=12,
<
30, то при оцінюванні гарантійного
(довірчого) інтервалу для похибки
середнього доцільно скористатися не
розподілом Гауса, а Стьюдента. За табл..
2 (додаток), що задає допустимі значення
гарантійного коефіцієнта для заданої
гарантійної (довірчої) ймовірності,
знайдемо відповідний коефіцієнт. А саме
для n=12,
 =0,95,
=0,95, =2,201.
Отже, результат вимірювання:
=2,201.
Отже, результат вимірювання:
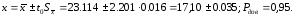
2.4 Оцінка результату опосередкованного вимірювання величини
Для оцінювання результату опосередкованого вимірювання величини U=Y2/X виконані по 9 вимірювань величин X та Y. Відомі СКВ похибок вимірювань цих величин σx та σy. Оцінити результат вимірювання U, вважаючи що результати вимірювань X, Y взаємно незалежні. Оцінити довірчі границі похибки вимірювання U з Рдов. Записати результат вимірювання.
Значення величин X, Y, σx, σy та Рдов див. в табл.4 відповідно до варіанта.
Таблиця 4. Дані до завдання 4:
|
Варіант |
Рдв |
Дані по Х |
σx | |||||||||
|
9 |
0,99 |
23,86 |
23,88 |
23,84 |
23,91 |
23,98 |
23,92 |
23,92 |
23,78 |
23,83 |
0.25 | |
|
Варіант |
Дані по Y |
σy | |||||||||
|
9 |
23,10 |
23,11 |
23,19 |
23,14 |
23,01 |
23,07 |
23,19 |
23,06 |
23,13 |
0.34 | |
Розв’язання
Похибку
опосередкованого вимірювання шукаємо
за похибками прямих вимірювань. Зокрема,
відносна похибка
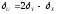 ,
а абсолютна похибка непрямого вимірювання
(див. задачу 3):
,
а абсолютна похибка непрямого вимірювання
(див. задачу 3):

Результати рівно точних взаємнонезалежних спостережень величин Х та У містять випадкові похибки. Тому найкращою оцінкою кожної з безпосередньо вимірюваних величин (Х та У) та опосередкованої величини U будуть їх середні значення, тобто:

За
визначенням абсолютна похибка
 тут
тут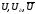 -
істинне, дійсне та середнє значення
величиниU,
яку можна оцінити значеннями
-
істинне, дійсне та середнє значення
величиниU,
яку можна оцінити значеннями
 за прямими спостереженнями
за прямими спостереженнями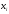 та
та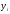 .
.
Тому дисперсія абсолютної похибки усередненого результату посереднього вимірювання:

Так само пов’язані і їх незміщені оцінки:

Своєю
чергою дисперсія похибок кожної з
усереднених величин
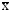 та
та дорівнює сумі незміщеної оцінки дисперсії
середнього випадкових спостережень та
дисперсії інструментальної похибки
відповідного вимірювального приладу,
а саме:
дорівнює сумі незміщеної оцінки дисперсії
середнього випадкових спостережень та
дисперсії інструментальної похибки
відповідного вимірювального приладу,
а саме:


Незміщені оцінки дисперсії спостережень:
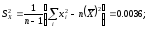

А
дисперсій відповідних середніх значень:
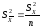 та
та
Звідси:



Для
 =0,99
йn=9
гарантійний коефіцієнт
=0,99
йn=9
гарантійний коефіцієнт
 .
Звідси результат опосередкованого
вимірювання:
.
Звідси результат опосередкованого
вимірювання:


2.5 Визначення коефіцієнтів лінійної залежності
Для результатів вимірювань величин X та Y за допомогою методу найменших квадратів визначити коефіцієнти лінійної залежності між ними.
Значення X та Y див. табл. 5 відповідно до варіанта.
Таблиця 5. Дані до завдання 5:
|
Варіант |
X |
Y | ||||||||||
|
9 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4.25 |
3.51 |
2.20 |
1.02 |
0.00 |
-1.20 |
Розв’язання
За умовою вважається, що залежність між величинами Y та Х є лінійною, тобто
Y=kX+b.
Необхідно знайти два невідомі параметри k й b, опрацьовуючи набори результатів спостережень {х,} та {у,} за методом найменших квадратів. Сформуємо відповідні рівняння, а саме: знайдемо часткові похідні функції Y за невідомими параметрами

Одержимо систему двох рівнянь з двома невідомими, а саме:


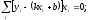


Звідси:





Знайдемо k=1,96; b=2,61. Отже Y=1,96; X=2,61.

Розрахунки реалізовані за допомогою математичного пакету Mathcad і наведені у додатку А.
2.6 Отримання результатів сукупних вимірювань, оцінка СКВ, знаходження нев’язок
Сформуйте систему нормальних рівнянь за методом найменших квадратів для результатів сукупних вимірювань. Оцінити СКВ. Знайти нев’язки. Записати результат вимірювання.
Результати сукупних вимірювань див. табл. 6 відповідно до варіанта.
Таблиця 6. Дані до завдання 6:
|
Варіант |
x1+x2x+x3+x4 |
x2+x3 |
x1+x2 |
x3+x4 |
x1+x2+x3 |
x1+x3+x4 |
x1+x4+x3 |
x2+x4 |
x3+x1 |
Pдов |
|
9 |
20,16 |
9,18 |
9,21 |
11,20 |
14,16 |
16,33 |
16,25 |
10,21 |
10,20 |
0,9 |
Розв’язання
Складемо систему нормальних рівнянь:
 ,
,
де коефіцієнти
 =
6,
=
6,
 =
5,
=
5,
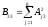 =
7,
=
7,
 =
5,
=
5,
 =
3,
=
3,
 =
5,
=
5,
 =
3,
=
3,
 =
2,
=
2,
 =
3,
=
3,
 =
4,
=
4,
 =
20,16+9,21+14,16+16,33+16,25+10,20=86,31
=
20,16+9,21+14,16+16,33+16,25+10,20=86,31
 =
20,16+9,18+9,21+14,16+10,21=62,92
=
20,16+9,18+9,21+14,16+10,21=62,92
 =
20,16+9,18+11,20+14,16+16,33+16,25+10,20 = 97,48
=
20,16+9,18+11,20+14,16+16,33+16,25+10,20 = 97,48
 =
20,16+11,20+16,33+16,25+10,21= 74,15.
=
20,16+11,20+16,33+16,25+10,21= 74,15.
Врахувавши значення даних коефіцієнтів система нормальних рівнянь матиме вигляд:
 .
.
Головний визначник цієї системи D = 156.
Найбільш ймовірні значення невідомих дорівнюють:
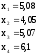
Підставляємо значення найбільш ймовірних значень до умовних рівнянь:
x1 + x2 + x3 + x4 = 5,08 + 4,05 + 5,07+ 6,1 = 20.3,
x2 + x3 = 4,05 + 5,07 = 9.12,
x1 + x2 = 5.08 + 4,05 = 9,13,
x3 + x4 = 5,07 + 6,1 = 11,17,
x1 + x2 + x3 = 5.08 + 4,05 + 5,07 = 14,2,
x1 + x3 + x4 = 5.08 + 5,07 + 6,1 = 16,25,
x1 + x3 + x4 = 5.08 + 5,07 + 6,1 = 16,25,
x2 + x4 = 4,05 + 6,1 = 10,15,
x1 + x3 = 5.08 + 5,07= 10,15.
Знаходимо нев´язки
 ,
,
Знайдемо границі довірчого інтервалу
 ,
,
і аналогічно для інших невідомих. Для цього розрахуємо значення ад’юнктів.
S11=70, S22=46, S33 = 72, S44 = 58

Для m-n=5 та ймовірності Р=0,95 коефіцієнт Ст´юдента дорівнює tp = 3,003
Розрахуємо границі довірчого інтервалу
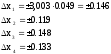
Отже, результат вимірювання

Розрахунки реалізовані за допомогою математичного пакету Mathcad і наведені у додатку Б.

