Електромагнетна індукція Основні формули

1. Робота переміщення замкнутого контура зі струмом в магнетному полі

,

де – зміна магнетного потоку, який пронизує поверхню,обмежену контуром;

І – сила струму у контурі.

2. Основний закон електромагнетної індукції (закон Фарадея)

,

де – електрорушійна сила індукції;

N – кількість витків контуру;

–потокозчеплення.

Окремі випадки застосування основного закону електромагнетної індукції:

• різниця потенціалів U на кінцях провідника довжиною l, який рухається зі швидкістю в однорідному магнетному полі

,

де а – кут між напрямками векторів швидкості та магнетної індукції В;

- електрорушійна сила індукції , яка виникає в рамці, що містить N витків площею S. При обертанні рамки з кутовою швидкістю в однорідному магнетному полі з індукцією В виникає електрорушійна сила

,

де – миттєве значення кута між векторомі векторомнормалі до площини рамки.

3. Заряд Q, який протікає в контурі

де R – опір контуру;

–зміна потокозчеплення

4. Електрорушійна сила самоіндукції , яка виникає у замкнутому контурі при зміні сили струму в ньому

або

де L – індуктивність контуру.

5. Потокозчеплення контуру

,

де L – індуктивність контуру.

6. Індуктивність соленоїда (тороїда):

де – кількість витків, які припадають на одиницю довжини соленоїда;

V – об'єм соленоїда.

У всіх випадках, для знаходження індуктивності соленоїда (тороїда) з сердечником з використанням наведеної формули для визначення магнетної проникності, слід користуватися графіком залежності В від Н, а потім формулою

.

7. . Миттєве значення сили струму І в колі, що має активний опір R та індуктивність L:

- після замикання кола

,

де – е.р.с. джерела струму;

t – час, що минув після замикання кола.

- після розмикання кола

,

де І₀ – значення сили струму в колі при t = 0;

t – час, що минув з моменту розмикання кола.

Приклади розв’язання задач

Приклад 1. У центрі плоскої колової дротяної рамки, яка складається з 50 витків радіусом 20 см, перебуває маленька рамка, яка складається з 100 витків площею 1 см². Маленька рамка обертається навколо одного з діаметрів великої рамки з постійною кутовою швидкістю 300 рад/с. Знайти максимальне значення ЕРС індукції, якщо в обмотці рамки тече струм силою 10 А.

Дано:

N₁ = 50

N₂ = 100

R = 20 см = 0,2 м

S =1 см² = 10^-4 м²

= 300 рад/с

I = 10 А

______________

_imax– ?

Розв’язання. При обертанні маленької рамки постійно змінюється кут  між вектором і нормаллю до площини рамки й, отже, змінюється магнетний потікФ, що пронизує маленьку рамку. У рамці виникає е.р.с. індукції, миттєве значення якої, за законом Фарадея, дорівнює

(1)

де  = N₂Ф – потокозчеплення.

Оскільки розміри маленької рамки малі в порівнянні з розмірами великої рамки, то поле в межах маленької рамки можна вважати однорідним. Магнетну індукцію В цього поля можна виразити через індукцію поля в центрі рамок

( 2)

Для однорідного поля магнетний потік, який пронизує маленьку рамку, дорівнює Ф = ВScos. З урахуванням того, що при обертанні рамки з постійною кутовою швидкістю миттєве значення кута =t, одержимо

Ф = ВS cos= BS cost.

Підставляючи у формулу (1) вираз для Ф і диференціюючи його за часом, знайдемо миттєве значення ЕРС індукції

ξ_i = N₂BS sint.

Максимальне значення ЕРС індукції дорівнює (sint=1)

ξ _{i max} = N₂BS.

З урахуванням (2), одержимо

.

Виразимо всі величини в одиницях СІ: R = 0,2 м; S = 10^-4 м²; I = 10 А;  = 300 рад/с; ₀ = 4^.10^-7 Гн/м;  = 1.

Виконавши обчислення, одержимо

Приклад 2. Контур у вигляді квадрата (рис.24) зі стороною 10 см перебуває в однорідному магнетному полі з індукцією 0,5 мТл так, що його площина становить кут 30^o з силовими лініями поля. Який заряд протече по контуру при вимиканні магнетного поля? Опір контуру 1 мОм.

Дано:

а= 10 см = 10^-1 м

В = 0,5 мТл = 5^.10^-4 Тл

α= 30^o

R =1 мОм = 1^.10^-3 Ом.

__________________

q – ?

Розв’язання. При вимиканні магнетного поля магнетний потік Ф, що пронизує контур, змінюється. У контурі виникає е.р.с. індукції, миттєве значення якої за законом Фарадея дорівнює Рисунок 24

.

Миттєве значення сили індукційного струму визначається за законом Ома

За час dt по контуру протече заряд

Інтегруючи цей вираз, знайдемо повний заряд

.

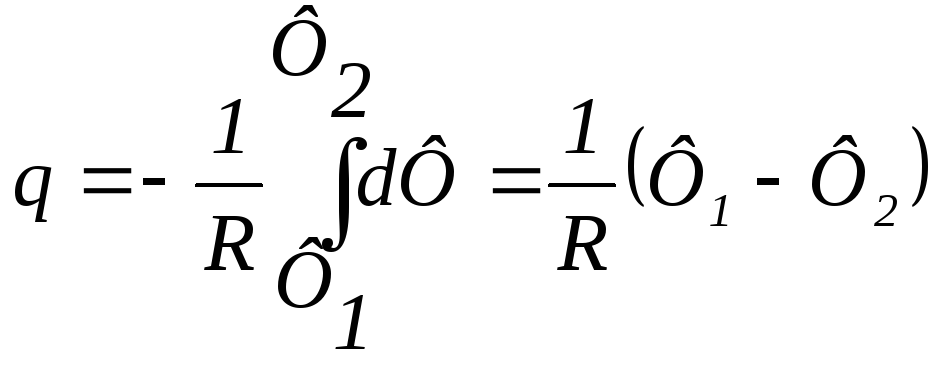Для однорідного магнетного поля початковий магнетний потік дорівнює

Ф₁ = BS cos,

де  – кут між вектором магнетної індукції і нормаллю до площини контура;

S = а² – площа квадрата.

З рисунка 23 видно, що  = 90^o – . Отже, cos = sin. Кінцевий магнетний потік Ф₂ = 0. Таким чином,

Виконавши необхідні обчислення, одержимо

Кл.

Приклад 3. Соленоїд із сердечником із немагнетного матеріалу містить 1200 витків, які щільно прилягають один до одного. При силі струму 4А магнетний потік, який створюється в соленоїді, дорівнює 4мкВб. Визначити індуктивність соленоїда й енергію його магнетного поля.

Дано:

N = 1200

I = 4 А

Ф = 4 мкВб = 4^.10^-6 Вб

_________________

L – ? W – ?

Розв’язування: Індуктивність соленоїда L пов'язана з потокозчепленням і силою струмуI співвідношенням

= LI . ( 1)

У свою чергу, потокозчеплення можна знайти через потік Ф и число витків N (якщо витки щільно прилягають один до одного)

= NФ . ( 2)

З формул (1) і (2) знаходимо індуктивність соленоїда

. ( 3)

Енергія магнетного поля соленоїда

.

Виразивши L згідно з (3), одержимо

.

Підставимо у формули значення фізичних величин і зробимо обчислення:

Дж = 14,4 мДж.