
- •С. Г. Авдєєв, т. І. Бабюк
- •Частина 1
- •Частина 1 Кінематика Основні формули
- •Приклади розв’язання задач
- •Динаміка прямолінійного руху Основні формули
- •Закони збереження. Робота й енергія Основні формули
- •Приклади розв’язання задач
- •Динаміка твердого тіла Основні формули
- •Приклади розв’язання задач
- •Гідростатика Основні формули
- •Електричне поле у вакуумі Основні формули
- •Електричне поле у діелектриках Основні формули
- •Провідники в електричному полі Основні формули
- •Енергія електричного поля Основні формули
- •Приклади розв’язання задач
- •Електричний струм Основні формули
- •Приклади розв’язання задач
- •Магнетне поле у вакуумі і середовищі Основні формули
- •Приклади розв’язання задач
- •Електромагнетна індукція Основні формули
- •Приклади розв’язання задач
- •Рух заряджених частинок в електромагнетному полі Основні формули
- •Додаток а Деякі відомості з математики
- •2. Формули диференціального й інтегрального числень
- •3. Формули для наближених обчислень
- •Довідкові дані
- •Сергій Григорович Авдєєв
Магнетне поле у вакуумі і середовищі Основні формули
Закон Біо-Савара-Лапласа
![]() ,
,
де dB – індукція магнетного поля, яку створює елемент провідника зі струмом;
![]() – магнетна
проникність;
– магнетна
проникність;
![]() – магнетна
стала (
– магнетна
стала (![]() 0=
4
0=
4![]() Гн/м);
Гн/м);
![]() –вектор,
який дорівнює за модулем довжині dl
провідника
і збігається за напрямком зі струмом у
провіднику);
–вектор,
який дорівнює за модулем довжині dl
провідника
і збігається за напрямком зі струмом у
провіднику);
I – сила струму;
![]() –радіус-вектор,
проведений від середини елемента
провідника до точки, в якій визначається
магнетна індукція.
–радіус-вектор,
проведений від середини елемента
провідника до точки, в якій визначається
магнетна індукція.
2.
Модуль вектора
![]() виражається
формулою
виражається
формулою
![]() ,
,
де
φ
– кут
між векторами
![]() і
і![]() .
.
3. Магнетна індукція поля довгого прямого провідника з струмом
![]() ,
,
де r0 – відстань від осі провідника до точки, у якій визначається магнетна індукція (рис.21).
При
симетричному розміщенні кінців провідника
відносно точки, в якій визначається
магнетна індукція (рис.22
а,б),
– cos![]() =
cos
=
cos![]() =
cos
=
cos![]() ,
а тому
,
а тому
![]() .
.
4. Магнетна індукція поля безмежно довгого провідника з струмом виражається формулою
![]()

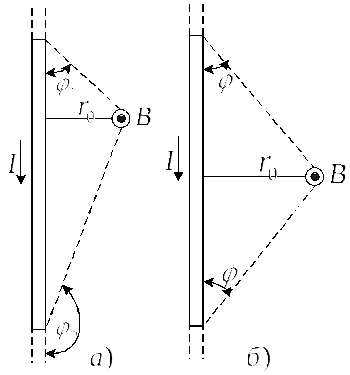
Рисунок 21 Рисунок 22
Позначення
зрозумілі з рис. 21.
Напрямок вектора
![]() збігається з дотичною до силової лінії,
напрям якої визначається правилом
правого гвинта.
збігається з дотичною до силової лінії,
напрям якої визначається правилом
правого гвинта.
5. Магнетна індукція В пов'язана з напруженістю H магнетного поля співвідношенням
![]()
або у вакуумі
![]() .
.
6. Магнетна індукція у центрі колового провідника зі струмом
![]() ,
,
де R – радіус кривизни провідника.
7. Магнетна індукція поля, яку створює соленоїд у середній його частині (або на осі тороїда)
![]() ,
,
де n – кількість витків, які припадають на одиницю довжини соленоїда або тороїда;
I – сила струму в одному витку.
8. Принцип суперпозиції магнетних полів. Магнетна індукція В результуючого поля дорівнює векторній сумі магнетних індукцій B1 , В2,...., Вn полів, що існують у даній точці, тобто
![]() .
.
У випадку накладання двох полів
![]()
а абсолютне значення вектора магнетної ідукції
![]()
де а – кут між векторами В1 і В2.
9. Закон Ампера. Сила, яка діє на провідник зі струмом в магнетному полі
![]() ,
,
де
I
– сила струму;
![]() – вектор, який дорівнює за модулем
довжині l
провідника і збігається за напрямком
зі струмом.
– вектор, який дорівнює за модулем
довжині l
провідника і збігається за напрямком
зі струмом.
Модуль вектора F визначається такою формулою:
![]() ,
,
де
а
– кут
між векторами
![]() і
і
![]() .
.
Сила взаємодії двох прямих нескінченно довгих паралельних провідників зі струмами І1 і І2, розміщених на відстані d один від одного, що діють на відрізок провідника довжиною l, виражається формулою
![]() .
.
Магнетний момент контуру зі струмом
![]() ,
,
де
![]() – вектор,
який дорівнює за модулем площі S,
яку
охоплює контур, і збігається за напрямком
з нормаллю до його площини.
– вектор,
який дорівнює за модулем площі S,
яку
охоплює контур, і збігається за напрямком
з нормаллю до його площини.
11. Механічний момент, який діє на контур зі струмом, розміщений в однорідному магнетному полі
![]() .
.
Модуль механічного моменту
![]() ,
,
де
а
– кут між векторами
![]() і
і
![]() .
.
12. Сила, що діє на контур зі струмом в магнетному полі (змінному вздовж осі х),
![]() ,
,
де
![]() – зміна магнетної індукції вздовж осіх,
розрахована
на одиницю довжини;
– зміна магнетної індукції вздовж осіх,
розрахована
на одиницю довжини;
а
– кут
між напрямками векторів
![]() і
і
![]() .
.
13. Закон повного струму для струму провідності: циркуляція вектора напруженості Н магнетного поля вздовж замкненого контуру, що охоплюється струмом І, виражається формулою
![]() ,
,
де Нl – проекція вектора Н на напрямок дотичної до контуру, що містить елемент dl;
І – сила струму, яка охоплюється контуром.
Якщо контур охоплює n струмів, то
![]()
де
![]() – алгебраїчна сума струмів, які охоплює
контур.
– алгебраїчна сума струмів, які охоплює
контур.
14. Магнетний потік Ф через плоский контур площею S:
- у випадку однорідного поля
![]() або
або
![]()
де
а
– кут
між вектором нормалі до площини контуру
і вектором магнетної індукції
![]() ;
;
Вn
– проекція
вектора
![]() на
нормаль
на
нормаль
![]() (Вn
=Bcosa);
(Вn
=Bcosa);
у випадку неоднорідного поля
![]() ,
,
де інтегрування ведеться через всію площу S.
15. Потокозчеплення, тобто повний магнітний потік, зчеплений зі всіма витками соленоїда або тороїда
![]() ,
,
де Ф – магнетний потік через один виток;
N – кількість витків соленоїда або тороїда.
16. Магнетна індукція на осьовій лінії тороїда
![]() ,
,
де І – сила струму в обмотці тороїда;
N – кількість витків в тороїді;
l – довжина середньої лінії сердечника тороїда;
![]() – магнетна
проникність речовини тороїда;
– магнетна
проникність речовини тороїда;
![]() –
магнетна
стала;
–
магнетна
стала;
Напруженість магнетного поля на осьовій лінії сердечника тороїда
![]() ;
;
магнетний потік в сердечнику тороїда
![]() ;
;
магнетний опір ділянки кола
![]() .
.
18.
Магнетна проникність
![]() феромагнетика, пов'язана з магнетною
індукцією В
поля
в ньому і напруженістю H
намагнечувального зовнішнього магнетного
поля співвідношенням:
феромагнетика, пов'язана з магнетною
індукцією В
поля
в ньому і напруженістю H
намагнечувального зовнішнього магнетного
поля співвідношенням:
![]() .
.
19. Зв’язок між магнетною індукцією поля В феромагнетика і напруженістю зовнішнього магнетного поля H, яке викликає намагнечування, виражається таким графіком.
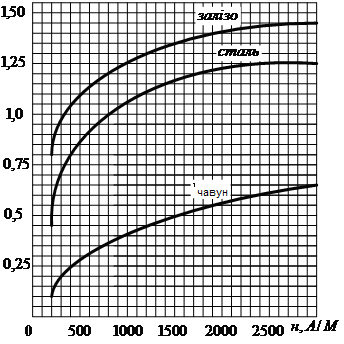
Графік залежності магнетної індукції поля
у магнетику від напруженості зовнішнього магнетного поля
