Свойства дифференциала

Пусть и – дифференцируемые в точке функции и , тогда:

1) 2)

3) 4)

5) 6)

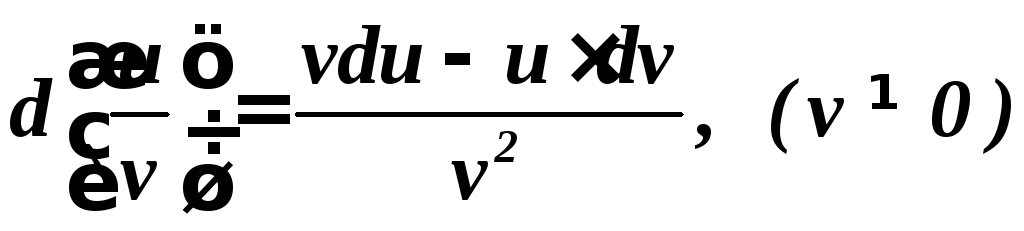
Замечания. 1. Так как =, то .

2. При достаточно малых приращениях , полное приращение функции , что используется в приближенных вычислениях.

Определение. Вторым дифференциалом (дифференциалом второго порядка) функции называется дифференциал от ее дифференциала, рассматриваемый как функция только основного аргумента (т.е. при постоянном ) и обозначается .

Найдем его выражение через вторую производную.

.

Аналогично вводится понятие дифференциала любого порядка.

Определение. Дифференциалом -го порядка некоторой функции называется дифференциал от дифференциала (-1)-го порядка, то есть .

Легко заметить, что . Откуда .

Пример 4. Пусть . Найти .

Решение. , .

.

2.2 Применение дифференциала в приближенных вычислениях

При достаточно малых полное приращение функции или , откуда

. (3)

Чем меньше , тем точнее эта формула. Абсолютная погрешность при замене функции ее дифференциалом вычисляется по формуле: , а относительная погрешность: .

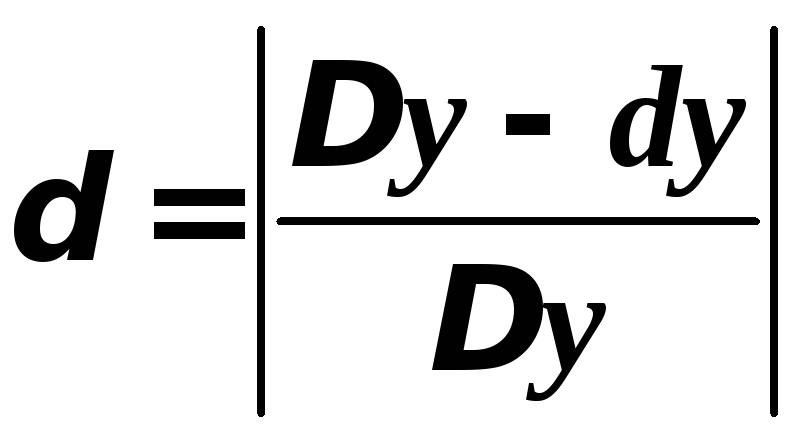Пример 1. Найти приращение и дифференциал функции при и . Вычислить абсолютную и относительную погрешности при замене приращения функции ее дифференциалом.

Решение. Определим и в общем виде.

.

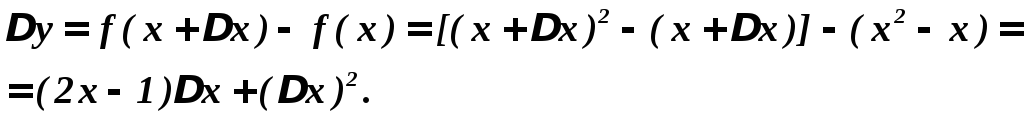
По условию и . Следовательно, .

Абсолютная погрешность , а относительная – 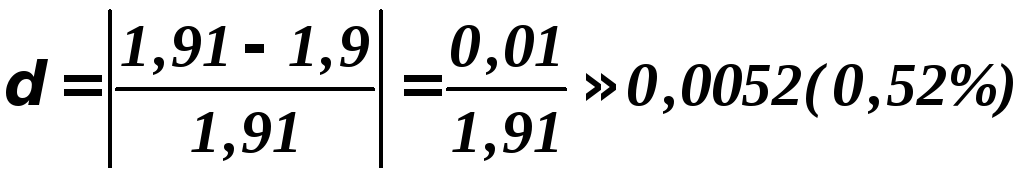. Таким образом, произвели оценку погрешности, допущенной при замене на

Пример 2. Вычислить приближенно .

Решение. Полагая , найдем и в соответствии с формулой (3) . Учитывая, что , возьмем и . Тогда

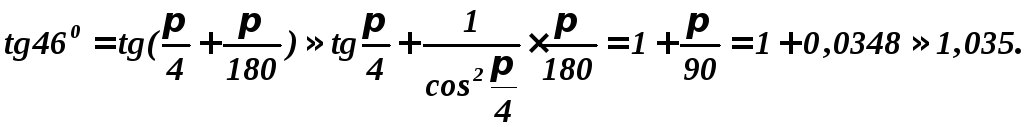
Замечание. Используя дифференциал, по формуле (3) легко получить формулы, часто используемые на практике при :

1. 2. 3.

4. 5. 6. 7.

и т.д.

Пример 3. Вычислить приближенно .

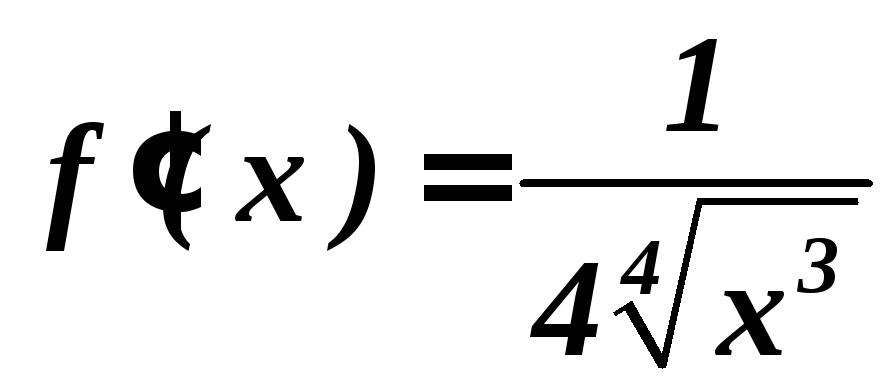Решение. Полагая , найдем и в соответствии с формулой (3) 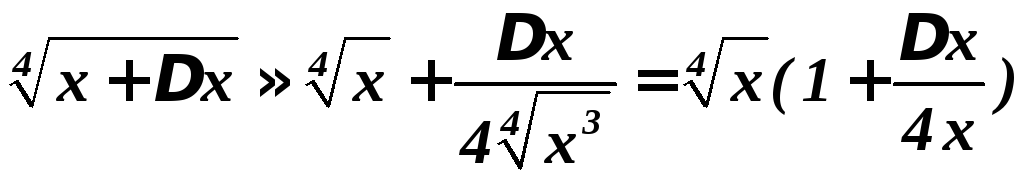. Учитывая, что , возьмем и . Тогда .

2.3. Теоремы о дифференцируемых функциях

Теорема Ферма. Если функция , определенная на , принимает в некоторой точке наибольшее или наименьшее значение и существует , то = 0.

Замечание. Геометрический смысл теоремы заключается в том, что внутри интервала в точке наибольшего или наименьшего значения касательная к графику функции в точке (,) параллельна оси .

Теорема Ролля. Если функция непрерывна на , дифференцируема на и =0, то существует такая точка , что =0.

Замечание. Геометрически теорему Ролля можно пояснить так: у функции , удовлетворяющей условиям теоремы, всегда существует внутренняя точка интервала , в которой касательная к графику функции параллельна оси .

Теорема Лагранжа. Если функция непрерывна на и дифференцируема на , то существует такая точка , что .

Замечание. Поясним геометрический смысл теоремы. У функции , удовлетворяющей условиям теоремы, всегда существует такая точка , что касательная к графику функции в точке (,) параллельна хорде, соединяющей концевые точки графика.

Теорема Коши. Если функции и непрерывны на и дифференцируемы на и , то существует такая точка , что .

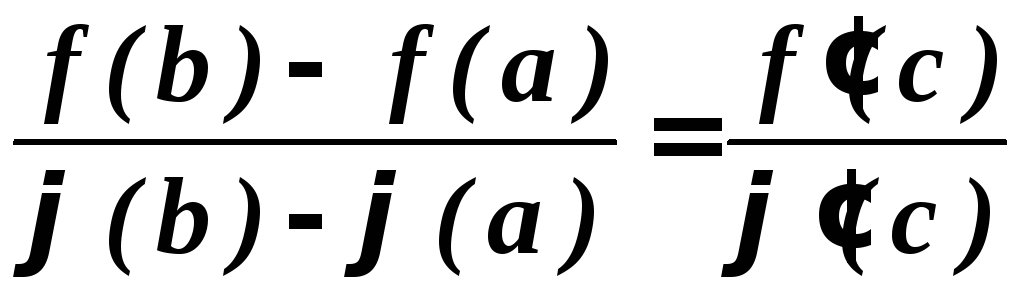Замечания: 1. Теорема Лагранжа является частным случаем теоремы Коши, когда ;

2. Приведенные теоремы носят, в основном, теоретический характер и будут использоваться далее при доказательстве других утверждений.