
- •Математика:
- •Текст печатается в авторской редакции Содержание
- •Предисловие
- •Методические рекомендации
- •Шкала оценок, правила вычисления рейтинга и возможности его повышения
- •Модульhо-рейтиhговая структура курса "математика”
- •Модульно-рейтинговая структура, график контроля в 1 семестре (корректируется для каждой специальности)
- •Модуль 3. Дифференциальное исчисление функции одной переменной
- •1. Производная функции
- •1.1. Задачи, приводящие к понятию производной
- •1.2. Геометрический смысл производной
- •1.3. Геометрические приложения производной
- •1.4. Связь между дифференцируемостью и непрерывностью. Правила дифференцирования
- •1.5. Таблица производных основных элементарных функций
- •1.6. Производная обратной и сложной функций
- •1.7. Производные высших порядков
- •1.8. Логарифмическое дифференцирование
- •1.9. Дифференцирование неявных функций
- •1.10. Дифференцирование функций, заданных параметрически
- •1.11. Аудиторные задания и задания на повышение рейтинга
- •Свойства дифференциала
- •2.2 Применение дифференциала в приближенных вычислениях
- •2.3. Теоремы о дифференцируемых функциях
- •2.4. Правило Лопиталя
- •2.5. Аудиторные задания и задания на повышение рейтинга
- •3. Исследование поведения функций и построение графиков
- •3.1. Необходимые и достаточные условия возрастания и убывания функции
- •3.2. Признаки существования экстремумов функции
- •Достаточные условия существования экстремума
- •Правило нахождения экстремумов функции
- •3.3. Асимптоты графика функции
- •Правило нахождения точек перегиба функции
- •3.5. Общая схема исследования функций и построения графиков
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •III. Исследование с помощью производной
- •IV. Нахождение дополнительных точек, уточняющих график
- •V. Построение графика функции
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •3.7. Аудиторные задания и задания на повышение рейтинга
- •Найти производную неявно заданной функции
- •3. Написать уравнения касательной и нормали к кривой
- •4. Найти второй дифференциал d2y функции
- •5. Вычислить предел , используя правило Лопиталя
- •6. Исследовать функцию и построить график
- •Решение типового варианта
- •Тестовое задание к модулю 3 "Дифференциальное исчисление функции одной переменной”
- •Образец текущего контроля к модулю 3
- •Теоретические вопросы
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
1.9. Дифференцирование неявных функций
Определение.
Функция
![]() называется
неявной
функцией
от
называется
неявной
функцией
от
![]() ,
если
она задана уравнением вида
,
если
она задана уравнением вида
![]() ,
не разрешенным относительно
,
не разрешенным относительно
![]() .
.
Для
нахождения производной
![]() нужно продифференцировать по
нужно продифференцировать по
![]() обе части равенства
обе части равенства
![]() ,
учитывая, что
,
учитывая, что
![]() есть сложная функция от
есть сложная функция от
![]() .
Затем разрешить полученное равенство
относительно искомой производной
.
Затем разрешить полученное равенство
относительно искомой производной
![]() ,
которая, как правило, будет зависеть от
,
которая, как правило, будет зависеть от
![]() и
и
![]() ,
т.е.,
,
т.е.,
![]() .
.
Пример
1.
Найти
уравнение касательной к окружности в
точке
![]() ,
если центр находится в начале координат
,
если центр находится в начале координат
![]() .
.
Решение.
Уравнение
окружности
![]() является неявной функцией. Найдем
производную этой функции:
является неявной функцией. Найдем
производную этой функции:
 Þ
Þ
 .
.
Уравнение
касательной имеет вид:
![]() =
=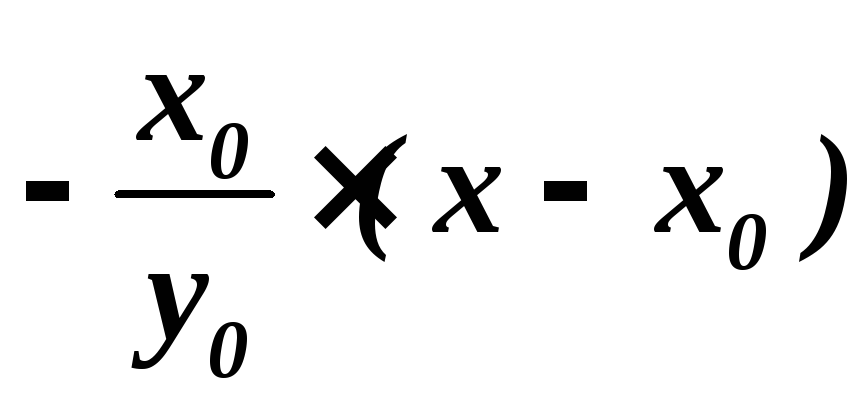 .
.
В
точке
![]() :
:
 .
.
Пример
2.
Найти производную функции
![]() ,
заданной уравнением
,
заданной уравнением
![]() .
.
Решение.
Логарифмируем обе части уравнения, а
затем дифференцируем, считая
![]() сложной функцией от
сложной функцией от
![]() .
.
![]()
![]()
![]()
![]()
Так
как
![]() сложная функция, то по правилу
дифференцирования сложной функции
имеем:
сложная функция, то по правилу
дифференцирования сложной функции
имеем:






Замечание.
Для нахождения второй производной
![]() неявной функции нужно продифференцировать
найденную первую производную
неявной функции нужно продифференцировать
найденную первую производную
![]() еще раз по
еще раз по
![]() ,
продолжая считать функцию
,
продолжая считать функцию
![]() ,
зависящей от
,
зависящей от
![]() .
В выражение второй производной при этом
войдут
.
В выражение второй производной при этом
войдут
![]() ,
,
![]() и
и
![]() ,
но, так как
,
но, так как
![]() известно, то, подставляя его в
известно, то, подставляя его в
![]() ,
найдем окончательное значение
,
найдем окончательное значение
![]() ,
зависящее только от
,
зависящее только от
![]() и
и
![]() .
Аналогично поступаем при нахождении
.
Аналогично поступаем при нахождении
![]() и т.д.
и т.д.
Пример
3.
Пусть
 (см. пример 1). Найти
(см. пример 1). Найти
![]() .
.
![]() =
= =
= .
.
1.10. Дифференцирование функций, заданных параметрически
Определение.
Уравнения
вида
 ,
где
,
где![]() параметр, называютсяпараметрическими
уравнениями.
параметр, называютсяпараметрическими
уравнениями.
Теорема.
Если
![]() и
и
![]() дифференцируемы по
дифференцируемы по
![]() и
и
![]() ,
то функция
,
то функция
![]() дифференцируема по
дифференцируема по
![]() и
и
 (1)
(1)
Полученная
производная является функцией от
параметра
![]() .
.
Применяя вторично правило дифференцирования функции, заданной параметрически, получим:
 . (2)
. (2)
Аналогично
поступаем при нахождении
![]() и т.д.
и т.д.
Пример
1.
Найти первую и вторую производные
функции
 .
.
Решение.
![]()
![]() .
Используя формулу (1), имеем:
.
Используя формулу (1), имеем:
 .
.
![]() ;
;
 .
Подставляя в формулу (2) найденные
производные, получаем:
.
Подставляя в формулу (2) найденные
производные, получаем:

1.11. Аудиторные задания и задания на повышение рейтинга
I. Найти производные следующих функций:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.![]() 6.
6.![]()
7.
![]() 8.
8.![]() 9.
9.![]()
10.
![]() 11.
11.![]() 12.
12.![]()
13.
![]() 14.
14.![]() 15.
15.![]()
16.
 17.
17. 18.
18.![]()
19.
![]() 20.
20.![]() 21.
21.![]()
22.
![]() 23.
23. 24.
24.![]()
25.
![]() 26.
26.![]() 27.
27.![]()
28.
![]() 29.
29. 30.
30.![]()
II.
Найти производные функций и вычислить
их значения при
![]() :
:
1.
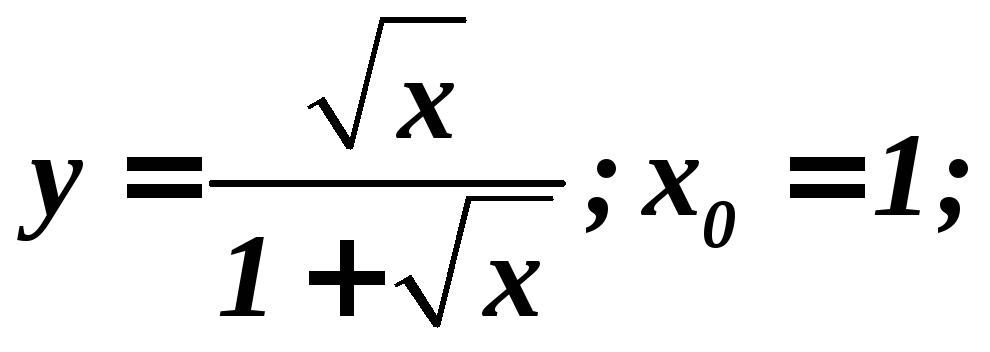 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
III. Найти производные следующих сложных функций:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.![]() 11.
11.
![]() 12.
12.
![]()
13.
 14.
14.
![]() 15.
15.
![]()
16.
 17.
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]() 21.
21.
![]()
22.
![]() 23.
23.

IV. Найти производные высших порядков следующих функций:
1.
![]()
![]() ?;
2.
?;
2.
![]()
![]() ?;
?;
3.
![]()
![]() ?;
4.
?;
4.
![]()
![]() ?;
?;
5.
![]()
![]() ?;
6.
?;
6.
![]()
![]() ?.
?.
V. Применив логарифмическое дифференцирование, найти производные следующих функций:
1.
 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
 10.
10.
 11.
11.
![]()
VI. Найти производные данных неявных функций:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
VII. Найти производные функций, заданных параметрически:
1.
 2.
2.
 3.
3.

4.
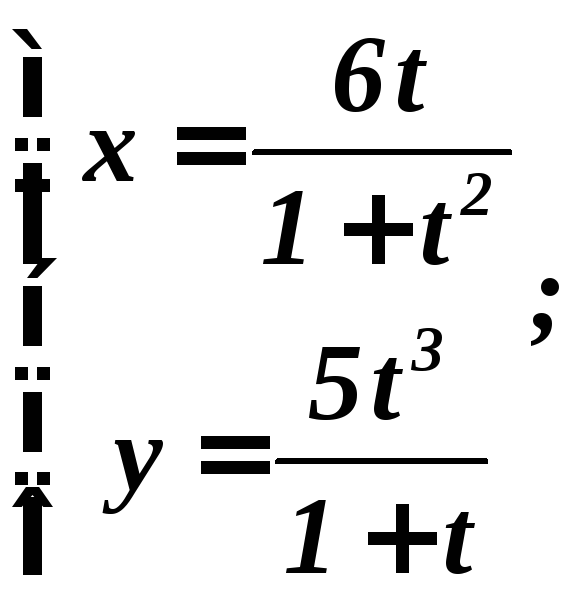 5.
5.
 6.
6.

2. Дифференциал функции. Свойства дифференцируемых функций
2.1. Дифференциал функции
Рассмотрим
дифференцируемую в точке
![]() функцию
функцию
![]() .
Из существования производной
.
Из существования производной
![]() =
=![]() следует, что
следует, что
![]() ,
где
,
где
![]() – бесконечно малая функция при
– бесконечно малая функция при
![]() ®0,
т.е.
®0,
т.е.
![]() =0.
Тогда полное приращение функции
=0.
Тогда полное приращение функции
![]() в точке
в точке
![]() равно
равно
![]() .
.
Определение.
Главная, линейная относительно
![]() ,
часть полного приращения функции
называется дифференциалом
функции
в точке
,
часть полного приращения функции
называется дифференциалом
функции
в точке
![]() и обозначается символом
и обозначается символом
![]() .
Для функции
.
Для функции
![]()
![]() .
Откуда
.
Откуда
![]() и, следовательно, дифференциал функции
и, следовательно, дифференциал функции
![]() .
.
Пример
1.
Найти дифференциал функции
![]()
Решение.
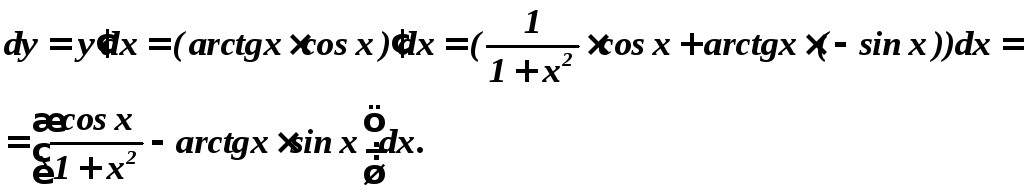
Пример
2.
Найти дифференциал функции
![]()
Решение.
![]()
Пример
3.
Найти дифференциал функции
![]() в точке
в точке
![]() .
.
Решение.
![]() ,
,
![]() .
.
Выясним геометрический смысл дифференциала.

Рис. 2.
На
рис. 2
![]() ,
,
![]() – касательная с угловым коэффициентом
– касательная с угловым коэффициентом
![]() .
Из прямоугольного треугольника
.
Из прямоугольного треугольника
![]() следует равенство:
следует равенство:
![]() .
Таким образом, дифференциал функции
.
Таким образом, дифференциал функции
![]() в точке
в точке
![]() равен приращению ординаты касательной,
проведенной к графику функции в точке
с абсциссой
равен приращению ординаты касательной,
проведенной к графику функции в точке
с абсциссой
![]() .
.
Теорема.
(Инвариантность
формы дифференциала).
Дифференциал
сложной функции
![]() ,
у которой
,
у которой
![]() ,
имеет такой же вид
,
имеет такой же вид
![]() ,
как и в том случае, когда аргумент
,
как и в том случае, когда аргумент
![]() является независимой переменной.
является независимой переменной.
