
- •Математика:
- •Текст печатается в авторской редакции Содержание
- •Предисловие
- •Методические рекомендации
- •Шкала оценок, правила вычисления рейтинга и возможности его повышения
- •Модульhо-рейтиhговая структура курса "математика”
- •Модульно-рейтинговая структура, график контроля в 1 семестре (корректируется для каждой специальности)
- •Модуль 3. Дифференциальное исчисление функции одной переменной
- •1. Производная функции
- •1.1. Задачи, приводящие к понятию производной
- •1.2. Геометрический смысл производной
- •1.3. Геометрические приложения производной
- •1.4. Связь между дифференцируемостью и непрерывностью. Правила дифференцирования
- •1.5. Таблица производных основных элементарных функций
- •1.6. Производная обратной и сложной функций
- •1.7. Производные высших порядков
- •1.8. Логарифмическое дифференцирование
- •1.9. Дифференцирование неявных функций
- •1.10. Дифференцирование функций, заданных параметрически
- •1.11. Аудиторные задания и задания на повышение рейтинга
- •Свойства дифференциала
- •2.2 Применение дифференциала в приближенных вычислениях
- •2.3. Теоремы о дифференцируемых функциях
- •2.4. Правило Лопиталя
- •2.5. Аудиторные задания и задания на повышение рейтинга
- •3. Исследование поведения функций и построение графиков
- •3.1. Необходимые и достаточные условия возрастания и убывания функции
- •3.2. Признаки существования экстремумов функции
- •Достаточные условия существования экстремума
- •Правило нахождения экстремумов функции
- •3.3. Асимптоты графика функции
- •Правило нахождения точек перегиба функции
- •3.5. Общая схема исследования функций и построения графиков
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •III. Исследование с помощью производной
- •IV. Нахождение дополнительных точек, уточняющих график
- •V. Построение графика функции
- •I. Исследование с помощью элементарной математики
- •II. Исследование с помощью теории пределов
- •3.7. Аудиторные задания и задания на повышение рейтинга
- •Найти производную неявно заданной функции
- •3. Написать уравнения касательной и нормали к кривой
- •4. Найти второй дифференциал d2y функции
- •5. Вычислить предел , используя правило Лопиталя
- •6. Исследовать функцию и построить график
- •Решение типового варианта
- •Тестовое задание к модулю 3 "Дифференциальное исчисление функции одной переменной”
- •Образец текущего контроля к модулю 3
- •Теоретические вопросы
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
Правило нахождения точек перегиба функции
Найти
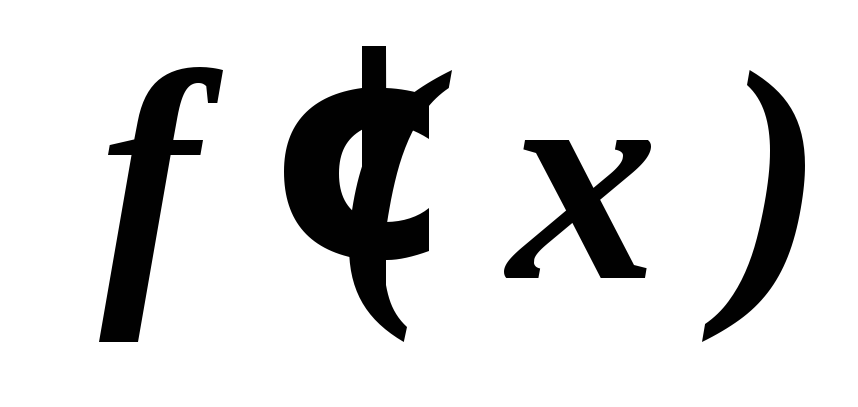 и
и
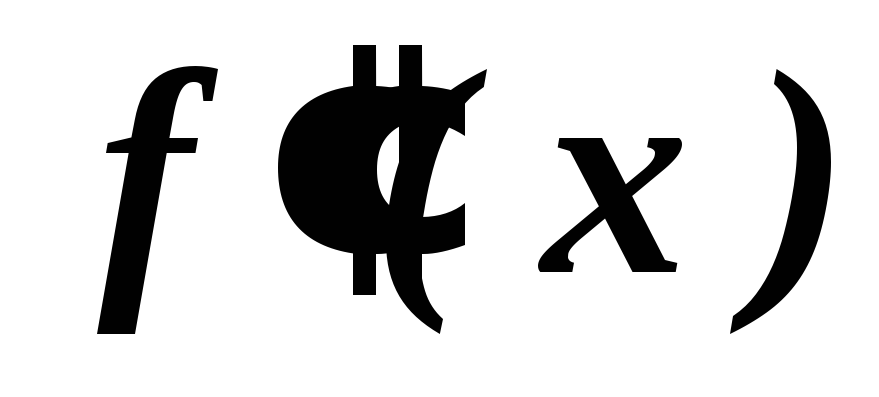 .
.Определить точки подозрительные на перегиб. Для этого нужно решить уравнение
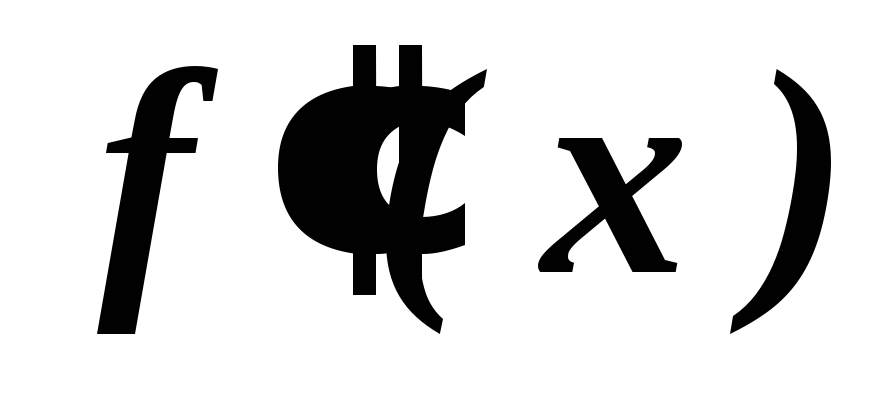 =
0
и найти точки, в которых
=
0
и найти точки, в которых
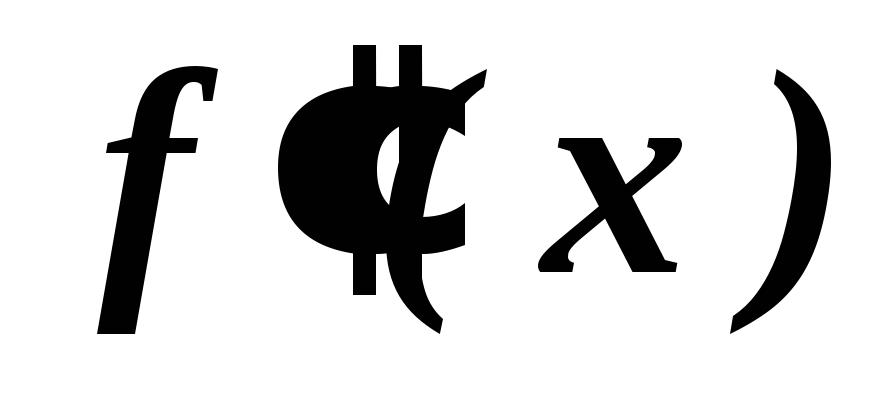 не существует, т.е. найти критические
точки второго рода.
не существует, т.е. найти критические
точки второго рода.Исследовать знак
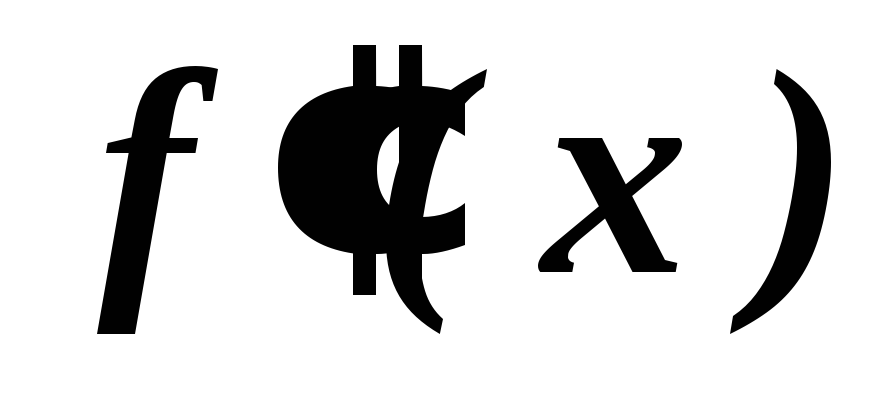 в окрестности критических точек и
сделать вывод об интервалах выпуклости
и наличии точек перегиба.
в окрестности критических точек и
сделать вывод об интервалах выпуклости
и наличии точек перегиба. Вычислить значения функции в точках перегиба, если они имеются.
Пример
1.
Найти
интервалы выпуклости и точки перегиба
функции
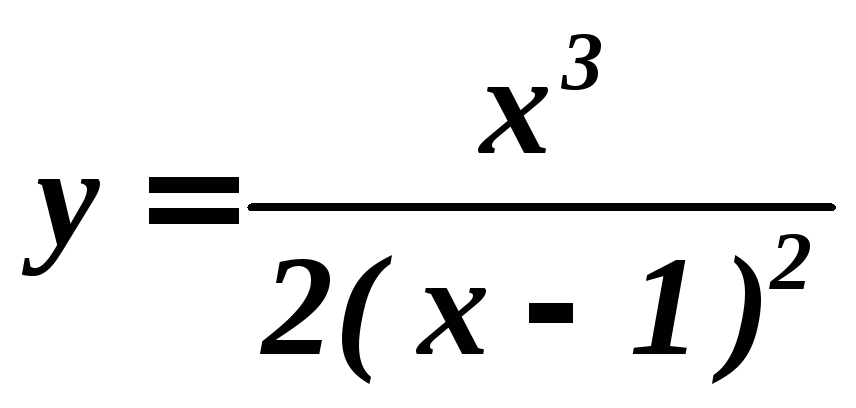 .
.
Решение.
1.
Исследование
проводится аналогично исследованию
(см. п.3.2) на существование точек экстремума.
Имеем,
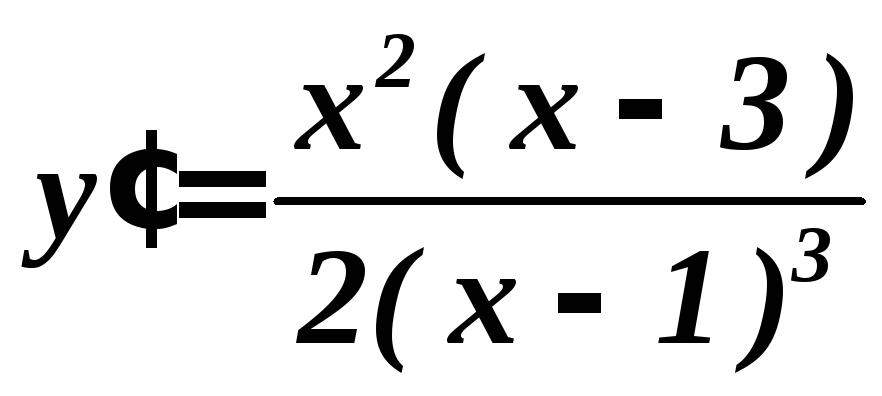 .
Найдем вторую производную
.
Найдем вторую производную
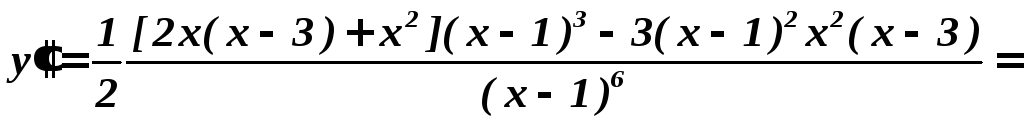
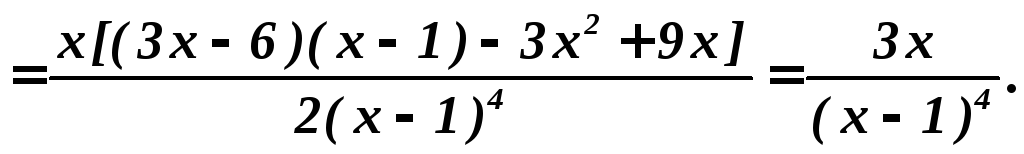
2. Найдем точки, в которых выполнено необходимое условие существования точек перегиба.
![]() =
0
Û
=
0
Û
![]() =
0,
откуда
=
0,
откуда
![]() =
0.
=
0.
![]() не
существует при условии
не
существует при условии
![]() =
0,
откуда находим
=
0,
откуда находим
![]() .
Следовательно,
.
Следовательно,
![]() =
0
и
=
0
и
![]() точки подозрительные на перегиб.
точки подозрительные на перегиб.
3.
Исследуем знак
![]() в окрестности этих точек.
в окрестности этих точек.
Удобно при исследовании использовать таблицу:
Таблица 2
-

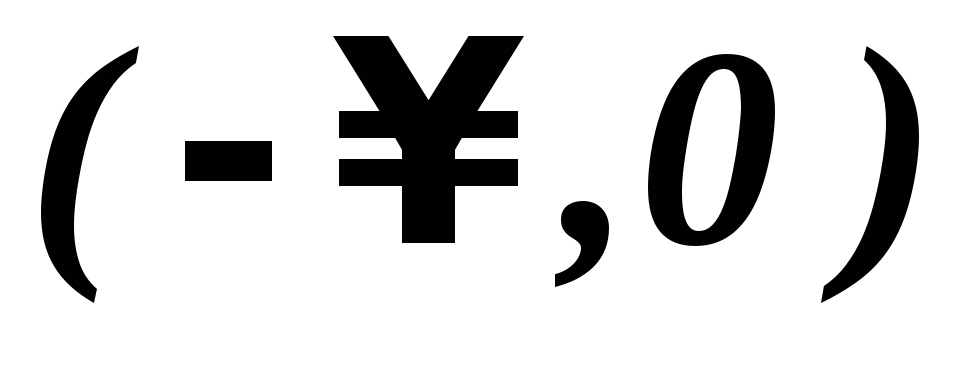
0
(0,1)
1
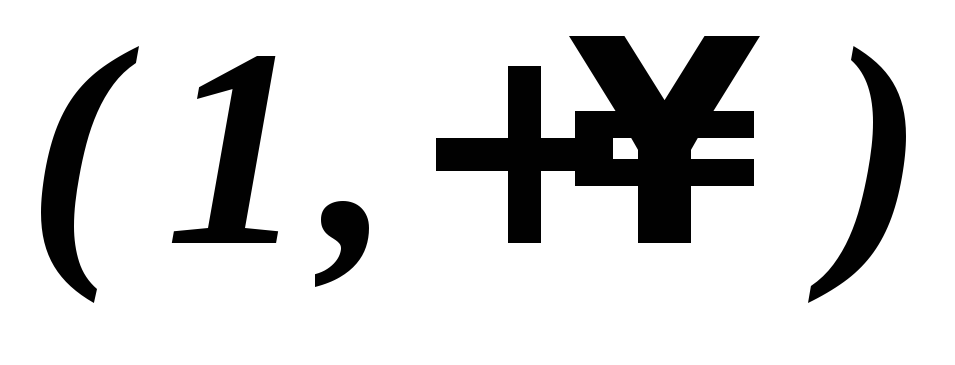
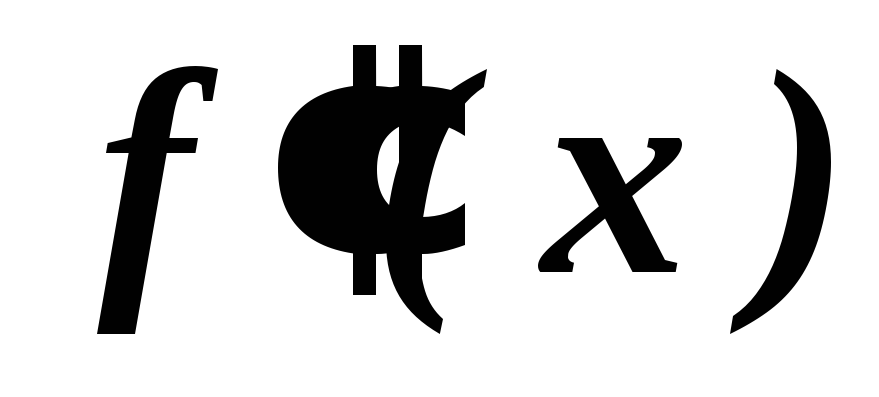
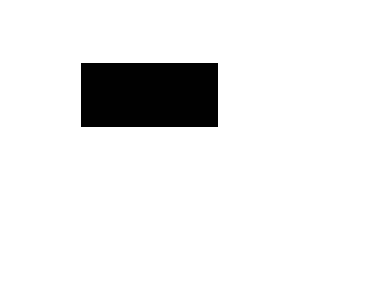
0
+
не сущ.
+
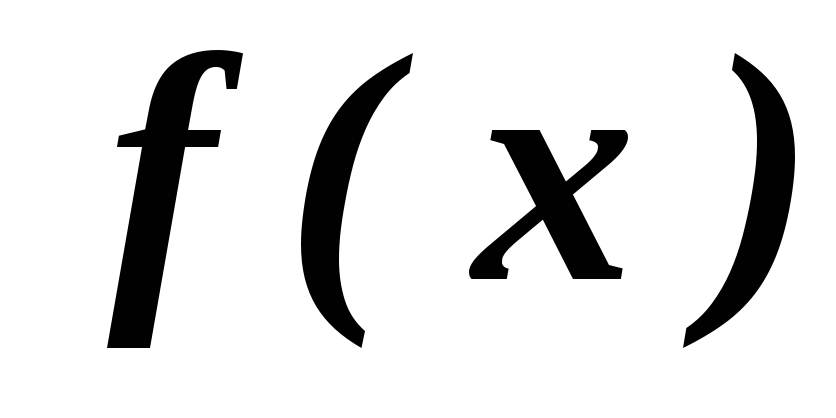
Ç
0
È
не сущ.
È
перегиб
Знаки
" + " и "
![]() " означают положительность и
отрицательность второй производной
" означают положительность и
отрицательность второй производной
![]() на соответствующем интервале. Дуги Ç
и È
означают выпуклость вверх (выпуклость)
и вниз (вогнутость) графика функции на
соответствующем интервале. Итак, график
исследуемой функции выпуклый вверх на
интервале
на соответствующем интервале. Дуги Ç
и È
означают выпуклость вверх (выпуклость)
и вниз (вогнутость) графика функции на
соответствующем интервале. Итак, график
исследуемой функции выпуклый вверх на
интервале
![]() и выпуклый вниз на интервалах (0,1)
и
и выпуклый вниз на интервалах (0,1)
и
![]() .
Точка
перегиба
.
Точка
перегиба
![]() =
0.
=
0.
4.
![]() .
.
3.5. Общая схема исследования функций и построения графиков
I. Исследование с помощью элементарной математики
1.
Найти область определения функции (![]() ).
).
2.
Найти область изменения функции (![]() ).
).
3.
Проверить функцию на четность или
нечетность (функция четная, если для
![]()
![]() ,
нечетная
,
нечетная
![]() если
если
![]()
![]() ,
если не выполняется ни то, ни другое
равенство, то функция общего вида, график
четной функции симметричен относительно
оси
,
если не выполняется ни то, ни другое
равенство, то функция общего вида, график
четной функции симметричен относительно
оси
![]() ,
нечетной – относительно начала
координат).
,
нечетной – относительно начала
координат).
4.
Проверить функцию на периодичность
(функция периодическая, если существует
такое число
![]() ,
что для
,
что для
![]() справедливо равенство
справедливо равенство
![]() ,
наименьшее из таких чисел
,
наименьшее из таких чисел
![]() называется периодом функции (обычно на
периодичность исследуются только
функции, содержащие тригонометрические
функции. Алгебраические и другие функции
периода не имеют)).
называется периодом функции (обычно на
периодичность исследуются только
функции, содержащие тригонометрические
функции. Алгебраические и другие функции
периода не имеют)).
5. Найти точки пересечения графика функции с осями координат.
6. Определить интервалы знакопостоянства.
II. Исследование с помощью теории пределов
7. Исследовать функцию на непрерывность, установить характер точек разрыва. Найти вертикальные асимптоты.
8. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
III. Исследование с помощью производной
9. Найти интервалы монотонности функции и точки экстремума.
10. Найти интервалы выпуклости функции и точки перегиба.
IV. Нахождение дополнительных точек, уточняющих график
V. Построение графика функции
Построение графика проводится по следующей схеме:
а) строим декартову систему координат на плоскости;
б) выбираем масштаб, соответствующий вычисленным значениям;
в) наносим на график точки пересечения графика функции с осями координат;
г) проводим пунктирной линией вертикальные, горизонтальные и наклонные асимптоты;
д) наносим на график точки экстремума и перегиба;
е) строим график функции, используя таблицы 1 и 2.
Пример
1.
Провести
полное исследование и построить график
функции
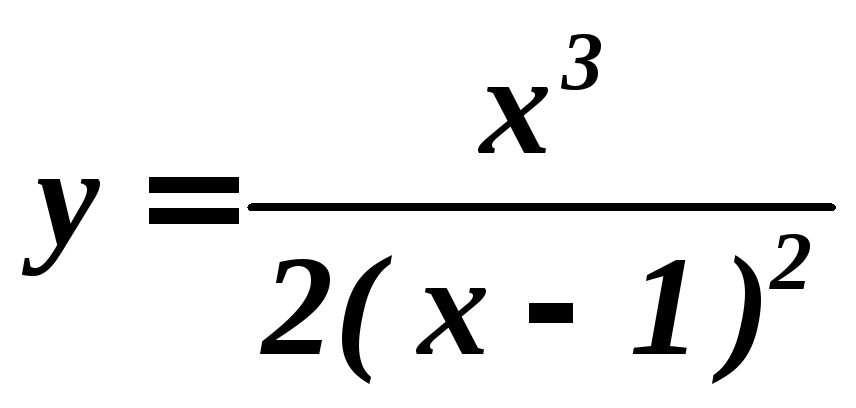 .
(см. примеры п. 3.2 , п. 3.3 и п. 3.4).
.
(см. примеры п. 3.2 , п. 3.3 и п. 3.4).
Решение.
