5 Электростатика

5.1 Краткие теоретические сведения

Электростатика – это физическая теория (раздел электродинамики), изучающая свойства неподвижных электрических зарядов и их взаимодействия посредством электростатических полей.

Электрические заряды делятся на положительные и отрицательные. Наименьшей устойчивой частицей, которая обладает отрицательным электрическим зарядом и входит в состав любого вещества, является электрон, положительным электрическим зарядом – протон. Электрический заряд протона и электрона называется элементарным зарядом и численно равен ≈ 1,6·10^–19 Кл. Электрический заряд любого заряженного тела равен целому числу элементарных зарядов.

Силы взаимодействия между заряженными телами зависят от их формы и размеров и характера распределения заряда на этих телах.

При изучении электростатических полей используют физическую модель – точечный заряд – это заряд, распределенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстояниями от него до других заряженных тел, с которыми он взаимодействует.

Сила электростатического взаимодействия точечных зарядов определяется законом Кулона: Сила взаимодействия двух точечных неподвижных зарядов прямо пропорциональна произведению модулей зарядов q₁ и q₂, обратно пропорциональна квадрату расстояния r между ними и зависит от свойств среды:

,

где – коэффициент пропорциональности;

–электрическая постоянная;

ε – диэлектрическая проницаемость среды.

Сила Кулона, направлена по прямой, соединяющей заряды, и подчиняется третьему закону Ньютона (F₁₂ = F₂₁), при этом одноименные заряды отталкиваются (рисунок 5.1а), разноименные – притягиваются (рисунок 5.1б).

Диэлектрическая проницаемость среды показывает во сколько раз сила электростатического взаимодействия двух точечных зарядов в вакууме F₀ больше силы взаимодействия в среде F_ср

.

Характеристики электростатического поля:

1. Напряжённость – это векторная физическая величина,характеризующая электростатическое поле и численно равная отношению силы, действующей на заряд q₀, помещённый в данную точку поля, к величине этого заряда:

; .

Направление вектора напряжённости совпадает с направлением силы, действующей на положительный заряд, помещенный в данную точку поля (противоположно направлению силы, действующей на отрицательный заряд, помещенный в данную точку поля) (рисунок 5.2).

2. Потенциал  – это скалярная физическая величина, характеризующая электростатическое поле и численно равная отношению потенциальной энергии заряда q₀, помещённого в данную точку поля, к величине этого заряда:

; .

Связь между характеристиками электростатического поля:

1. в общем случае:

;

2. для поля, обладающего центральной или осевой симметрией:

;

3. для однородного поля:

.

Знак «–» показывает, что напряженность электростатического поля направлена в сторону убывания потенциала.

Модуль вектора напряжённости и потенциал поля точечного заряда q в некоторой точке поля, удаленной от заряда на расстояние r

, .

Каждый электрический заряд создает в пространстве электростатическое поле независимо от наличия других электрических зарядов, поэтому, если в данной точке электростатическое поле создано не одним точечным зарядом, а системой зарядов, то, согласно принципу суперпозиции (наложения) электростатических полей:

1. Напряжённость результирующего поля системы зарядов равна геометрической сумме напряженностей полей каждого заряда в отдельности (рисунок 5.3):

.

В зависимости от взаимного расположения векторов и(рисунок 5.3) модуль напряженности результирующего поля может быть найден различным образом:

а) Если векторы ирасположены вдоль одной прямой и направлены в одну сторону (рисунок 5.3а), то модуль напряженности результирующего

поля находится по формуле

.

б) Если векторы ирасположены вдоль одной прямой и направлены в противоположные стороны (рисунок 5.3б), то модуль напряженности результирующего поля находится по формуле

,

вектор направлен в сторону большего по модулю из векторови.

в) Если векторы иобразуют прямоугольный треугольник (рисунок 5.3в), то модуль напряженности результирующего поля находится по теореме Пифагора

г) Если векторы иобразуют произвольный треугольник (рисунок 5.3г), то модуль напряженности результирующего поля находится по теореме косинусов

,

где  – угол, противолежащий стороне Е_А;

 = π – , где  – угол между векторами и.

2. Потенциал результирующего поля системы зарядов равен алгебраической сумме потенциалов полей каждого заряда в отдельности:

.

5.2 Пример выполнения задания

Задача 1:

Два неподвижных точечных заряда q₁ = 1нКл и q₂ = – 2нКл находятся в воздухе на расстоянии r = 10 см друг от друга. Определить напряженность и потенциал поля этих зарядов в точке А, удаленной от заряда q₁ на расстояние r₁ = 9 см и от заряда q₂ на расстояние r₂ = 7 см (рисунок 5.4).

Решение:

1. Согласно принципу суперпозиции электростатических полей, напряженность результирующего поля в исследуемой точке А равна

,

где – вектор напряженности поля точечного зарядаq₁ в точке А;

–вектор напряженности поля точечного заряда q₂ в точке А.

Для определения направления векторов ив исследуемую точку А «мысленно» помещают пробный положительный зарядq₀ и рассматривают силы взаимодействия между зарядами q₀ и q₁, q₀ и q₂. Направление вектора напряженности совпадает с направлением силы Кулона, действующей со стороны зарядаq₁ на заряд q₀; направление вектора напряженности совпадает с направлением силы Кулона, действующей со стороны зарядаq₂ на заряд q₀; направление вектора напряженности результирующего поля определяется геометрическим сложением векторовипо правилу параллелограмма.

Модуль вектора напряженности Е_А результирующего поля найдем, используя теорему косинусов для треугольника со сторонами Е₁, Е₂ и Е_А:

, (5.1)

где Е₁ – модуль напряженности поля точечного заряда q₁ в точке А,

, (5.2)

Е₂ – модуль напряженности поля точечного заряда q₂ в точке А,

, (5.3)

 – угол между сторонами Е₁ и Е₂.

Из чертежа (рисунок 5.4) видно, что угол  может быть также найден с помощью теоремы косинусов, записанной для треугольника со сторонами r₁, r₂ и r:

.

В данной задаче во избежание громоздких записей удобно значение cos  вычислить отдельно:

.

Подставляя выражения (5.2) и (5.3) в выражение (5.1) и вынося общий множитель за скобки и из-под знака корня, получим

. (5.4)

2. Согласно принципу суперпозиции электростатических полей, потенциал результирующего поля в исследуемой точке А равен

, (5.5)

где ₁ – потенциал поля точечного заряда q₁ в точке А,

, (5.6)

₂ – потенциал поля точечного заряда q₂ в точке А,

. (5.7)

Подставляя выражения (5.6) и (5.7) в выражение (5.5) и вынося общий

множитель за скобки, получим

. (5.8)

3. Произведем вычисления:

.

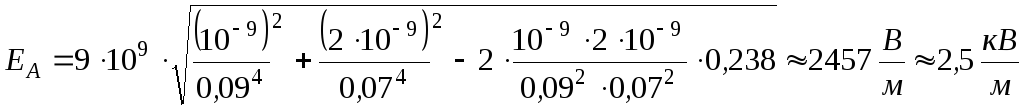–162 В.

Ответ: Е_А = 2,5 кВ/м, _А = –162 В.

Задача 2:

По тонкой нити, изогнутой по дуге окружности радиусом R = 15 см, равномерно распределён заряд с линейной плотностью τ = 10 нКл/м. Определить напряжённость Е и потенциал  поля нити в точке О, совпадающей с центром кривизны дуги. Длина нити ℓ составляет 1/3 длины окружности.

Решение:

1. Сделаем чертёж (рисунок 5.5): выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Oy была бы симметрично расположена относительно концов дуги.

Разобьём нить на элементарные участки длины dℓ, каждый из которых обладает зарядом dq =τ dℓ, который можно считать точечным.

2. Каждый электрический заряд dqсоздает в точке О электростатическое поле напряженностьюнезависимо от наличия других электрических зарядов исогласно принципу суперпозиции (наложения) электростатических полей, напряженностьполя нити в точке О равна

(интегрирование ведется вдоль дуги длинойℓ). (5.9)

Разложим вектор на составляющие вдоль координатных осей

. (5.10)

Тогда, подставляя выражение (5.10) в выражение (5.9), получим

.

Однако в силу симметрии , поэтому. (5.11)

Учитывая, что все вектора направлены в одну сторону (вдоль оси Оy), то выражение (5.11) можно переписать в скалярном виде

, (5.12)

где . (5.13)

Модуль напряженности поля точечного заряда dq в точке О определяется по формуле

. (5.14)

Учитывая связь линейного и углового перемещений (d – измеряется в радианах) и, подставляя выражение (5.14) в выражение (5.13), получим

. (5.15)

Так как длина нити составляет 1/3 длины окружности, то угол  изменяется в пределах

. (5.16)

Тогда, подставляя выражение (5.15) в выражение (5.12) и учитывая выражение (5.16) в качестве пределов интегрирования, получим

.