Метод наименьших квадратов

При проведении эксперимента часто требуется проследить зависимость одной физической величины от другой, например, y = f(x). Для этого производят ряд наблюдений искомой величины y для различных значений величины x. Затем найденные значения откладывают на графике и пытаются найти кривую, соответствующую алгебраической функции y = f(x), которая проходит как можно ближе к точкам.

Теория вероятностей показывает, что наилучшим приближением будет такая кривая (или прямая) линия, для которой сумма квадратов отклонений (расстояний) по вертикали от экспериментальных точек до кривой будет минимальной. Такой метод обработки экспериментальных данных называется методом наименьших квадратов.

Ограничимся рассмотрением применения метода наименьших квадратов для обработки результатов измерений в случае аппроксимации линейной зависимостью у = ах + b.

Линейная зависимость очень широко распространена в естественных и социально-экономических науках. И даже когда зависимость нелинейная, обычно выбирают величины, откладываемые по осям, таким образом, чтобы получить прямую линию. Например, график пути S от времени t при равнопеременном движении строят в осях S = f(t²), частоту собственных колебаний струны ν от натяжения струны Р – в осях ν = f(P^1/2), энергетическую светимость тела R_э, от его температуры Т – в осях R_э = f(T ⁴).

В рассматриваемом случае для построения аппроксимирующей прямой y = ax + b необходимо найти значения углового коэффициента а и параметра b.

При выводе предположим, что ошибки содержат только величины y_i(такое предположение часто оправдывается на практике), иначе вывод значительно усложнится.

Пусть отклонение по вертикали экспериментального значения y_iот аппроксимирующей прямойу = ах + bвi-ом (i = 1, 2, 3, ... , n) измерении (прих = x_i) равно

,

тогда, согласно методу наименьших квадратов наилучшим приближением будет такая аппроксимирующая прямая, для которой сумма квадратов отклонений по вертикали от экспериментальных точек до прямой по всем n измерениям будет минимальной, т.е.

 – минимальна.

Для определения значений коэффициентов а и b аппроксимирующей прямой, при которых величина S будет минимальной, найдем частные производные ии приравняем их к нулю.

Составим систему уравнений:

; (2.1)

Учитывая, что а = Const и b = Const, и, разделив каждое из уравнений системы (2.1) на 2, получим

(2.2)

Коэффициенты а и b найдём решением системы уравнений (2.2).

Для нахождения коэффициента а, умножим первое уравнение системы (2.2) на n, а второе – на :

(2.3)

Вычтем второе уравнение системы (2.3) из первого и получим:

,

откуда коэффициент а:

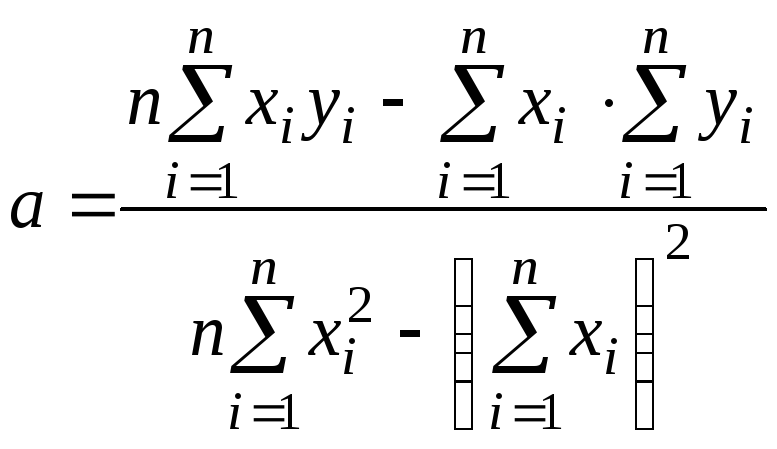. (2.4)

Для нахождения коэффициента b, умножим первое уравнение системы (2.2) на , а второе – на:

(2.5)

Вычтем первое уравнение системы (2.5) из второго и получим:

,

откуда коэффициент b:

. (2.6)

Очевидно, что ручная обработка результатов с помощью приведённых формул слишком трудоёмка. При построении графиков "вручную" метод наименьших квадратов используется интегрировано – прямая между экспериментальными точками проводится "на глаз".

2.2 Пример выполнения задания

Задача:

Экспериментально снята зависимость величины у от величины х (значения х и соответствующие им экспериментальные значения у приведены в таблице 2.1). Методом наименьших квадратов определить коэффициенты а и b аппроксимирующей линейной зависимости у = ах + b. На системе координат XOY проставить экспериментальные точки и построить график аппроксимирующей зависимости.

Дано:

Таблица 2.1 – Экспериментальные данные

x	0	1	2	3	4	5	6	7	8	9
y	2,0	2,4	2,5	3,2	3,8	4,2	4,1	5,0	5,4	6,0

Решение:

Коэффициенты а и b для построения аппроксимирующей линейной зависимости у = ax + b найдем методом наименьших квадратов, используя готовые формулы (2.4) и (2.6).

Для удобства вычислений заполним таблицу:

i	1	2	3	4	5	6	7	8	9	10
xi	0	1	2	3	4	5	6	7	8	9	45	2025
xi2	0	1	4	9	16	25	36	49	64	81	285	–
yi	2,0	2,4	2,5	3,2	3,8	4,2	4,1	5,0	5,4	6,0	38,8	–
xiyi	0	2,4	5,0	9,6	15,2	21,0	24,6	35,0	43,2	54,0	210	–

где

;

;

;

;

.

Тогда, учитывая, что число измерений n = 10, по формулам (2.4) и (2.6) найдём коэффициенты а и b аппроксимирующей линейной зависимости:

;

.

Следовательно, аппроксимирующая линейная зависимость имеет вид

у = 0,44x + 1,88.

Для построения аппроксимирующей зависимости найдем координаты двух точек А и В, принадлежащих прямой:

	А	В
x	0	9
y	1,88	5,84

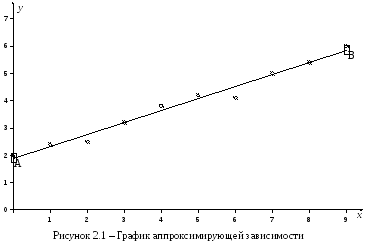
На системе координат XOY проставим экспериментальные точки (обозначены символом «○») и построим график аппроксимирующей зависимости по точкам А и В (обозначены символом «») (рисунок 2.1).