§3. Задача о кратчайшем пути

Исторически сложились три задачи о поиске пути в графе.

Задача 1. Найти любой путь (цепь) из А в В.

Задача 2. Найти кратчайший путь из А в В в смысле количества ребер (дуг).

Алгоритм решения задачи о нахождении кратчайшего пути из А в В в смысле наименьшего количества ребер:

1. Вершине А припишем индекс 0.

2. Всем вершинам, смежным с А, припишем индекс 1.

3. Всем вершинам, смежным с вершинами индекса 1 и не имеющим индекса, припишем индекс 2 и т.д.

4. Как только вершина В получит некоторый индекс, процесс присвоения останавливается. Значение индекса n вершины В и есть длина кратчайшего пути из А в В. Построим этот путь.

5. Среди вершин, смежных с В, обязательно найдется вершина с индексом n-1 (одна или несколько), возвращаемся в эту вершину и продолжаем этот процесс.

6. Через n шагов придем в вершину с индексом 0, т.е. в А. Один или несколько путей построены.

Если каждому ребру (дуге) графа приписано некоторое число _k0 (вес ребра), то граф называется взвешенным (нагруженным)

Задача 3. Найти кратчайший путь из А в В во взвешенном графе (в смысле суммы весов ребер (дуг)).

Приведем алгоритм решения задачи 3.

Будем постепенно приписывать всем вершинам графа числовые индексы:

1. Вершине А припишем индекс 0, всем остальным вершинам значение +.

2. Будем постепенно перебирать все пары смежных вершин v_x и v_y. Каждый раз проверим первенство , если оно

   v_y

3. выполняется, то уменьшаем индекс 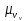, заменив его на.

v_x

4. Процесс останавливаем, когда ни один индекс уже нельзя уменьшить. В этот момент вершина В имеет некий индекс . Это и есть наименьшая сумма весов всех дуг.

5. Построим путь с такой суммой. Будем возвращаться из вершины В в А. Среди вершин, смежных с В, обязательно найдется вершина С, для которой выполняется точно равенство _В=_С+_СВ.

Возвращаемся к С и повторяем процесс. Поскольку индексы все время уменьшаются, то через несколько шагов придем в вершину с индексом 0, т.е. вершину А.

Примеры решения задач

Задача 1. Задан граф.

v₆

v₇

v₅

v₂

v₈

v₁

v₄

v₃

Найти кратчайший путь из вершины v₁ в вершину v₈.

Решение. Используя алгоритм задачи о нахождении кратчайшего пути из v₁ в v₈ в смысле наименьшего количества ребер, получим:

1. Вершине v₁ припишем индекс 0.

2. Всем вершинам, смежным с v₁ (v₂ и v₃), припишем индекс 1.

3. Всем вершинам, смежным v₂ и v₃ и не имеющим индекса (v₅,v₄,v₆,v₇), припишем индекс 2.

4. Всем вершинам, смежным с вершинами (v₄,v₅,v₆,v₇) и не имеющим индекса v₈, припишем индекс 3.

Таким образом, вершина v₈ получила индекс 3, а значит, длина кратчайшего пути из v₁ в v₈ равна 3. Построим этот путь или пути, если их несколько.

5. Среди вершин, смежных с v₈, найдем вершины с индексом 3-1=2. Таких вершин три: v₆,v₇, v₄.

6. Среди вершин, смежных с v₄,v₆,v₇, найдем вершины с индексом 1. Таких вершин две: v₂ и v₃.

7. Среди вершин, смежных с v₂ и v₃, найдем вершины с индексом 0. Такая вершина одна и это v₁.

Таким образом, было получено три кратчайших пути длины 3. Перечислим их: 1) v₁,v₂,v₆,v₈; 2) v₁,v₃,v₇,v₈; 3) v₁,v₃,v₄,v₈.

v₆ (2)

v₇ (2)

v₅ (2)

v₂ (1)

v₈ (3)

v₁ (0)

v₄ (2)

v₃ (1)

Задача 2. Задан орграф.

4

v₅

v₂

2

5

3

1

6

2

v₆

v₄

v₁

5

1

2

1

v₇

3

v₃

Найти кратчайший путь из вершины v₁ в вершину v₆ в смысле суммы весов дуг.

Решение. Используя алгоритм решения задачи о нахождении кратчайшего пути в смысле суммы весов дуг, получим:

1. Вершине v₁ присвоим индекс 0, а всем остальным +.

2. Переберем вершины орграфа, смежные с вершиной v₁ и имеющие дугу из v₁ в эту же вершину. Вершине v₄ присвоим индекс 0+2=2, так как 2<+. Вершине v₃ присвоим индекс min {0+1, 2+2}=1, так как 1<+. Вершине v₂ присвоим индекс min{0+1, 2+5}=2, так как 1<+.

3. Аналогично проведем рассуждения для вершин орграфа, смежных с вершинами v₂,v₃,v₄. Так как в вершину v₅ ведет две дуги, то присвоим ей индекс min{1+4, 2+3}=5<+. Вершине v₇ присвоим индекс min{2+5, 1+3}=4<+.

4. Вершине v₆ присвоим индекс min{5+2, 2+6, 4+1}=4+1=5. Таким образом, кратчайший путь из вершины v₁ в v₆ в смысле суммы весов дуг равен 5.

Построим этот путь.

5. Среди вершин, смежных с вершиной v₆, найдем вершину С, для которой выполняется равенство . Такой вершиной являетсяv₇, так как или 4+1=5.

6. Среди вершин, смежных с вершиной v₇, найдем вершину Д, для которой выполняется равенство . Такой вершиной являетсяv₃, так как или 1+3.

7. Среди вершин, смежных с вершиной v₃, найдем такую вершину Е, для которой выполняется равенство . Такая вершина одна и этоv₁.

Таким образом, мы вернулись из вершины v₆ в вершину v₁.

Запишем кратчайший путь из v₁ в v₆: v₁ v₃ v₇ v₆.

v₅ (5)

v₂ (1)

2

5

3

1

6

2

v₆

v₄(2)

v₁ (0)

5

1

2

1

3

v₇(4)

v₃ (1)