Задачи для самостоятельного решения

Задача 1. .

Решение. .

Задача 2. f(x)=.

Решение. f*=. Следовательно, данная функция самодвойственна.

§5. Функциональная полнота. Теорема Поста

Функциональный набор логических функций это такой набор функций, который позволяет любую функцию математической логики описать с помощью функции данного набора.

Теорема Поста. Для того чтобы набор функций f(x₁, …, x_n) был функционально полным, необходимо и достаточно, чтобы для всего набора функций в целом не выполнялось свойство сохранения нуля, сохранения единицы, линейность, монотонность и самодвойственность. Полноту набора функций удобно определять по таблице Поста, в котором знаком + или – обозначаются функции, принадлежащие (+) или не принадлежащие (-) к одному из этих классов.

В силу теоремы Поста, для полноты системы необходимо и достаточно, чтобы в каждом столбце таблицы Поста был хотя бы один минус.

Примеры решения задач

Задача 1.

F={f₁,f₂}

	P0	P1	L	M	S
f1	+	+	-	+	+
f2	-	+	-	-	-

Решение. Так как f₁ и f₂ Р₁, следовательно, {f₁,f₂} не является полной.

Задача 2. Выяснить, является ли система функций f₁=x1 и f₂=(x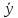)x полной.

Решение. f₁=x11

x	f
0	1
1	1

f₂=(x)x

x	y	x	f
0	0	0	1
0	1	1	1
1	0	1	0
1	1	0	1

Составим таблицу Поста

	P0	P1	L	M	S
f1	-	+	+	+	+
f2	-	+	-	-	-

f₂=(x)x

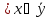=Многочлен Жегалкина второй степени линейностью не обладает, так как таблица содержит столбец со всеми плюсами, то исходная система булевых функций по теореме Поста не является полной.

Задачи для самостоятельного решения

Задача 1. Проверить на монотонность булеву функцию f=(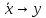)(z).

Задача 2. Проверить на линейность булеву функцию f=(x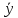)(z).

Задача 3. Проверить на полноту систему булевых функций

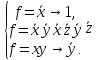1. 2) , 3)

Список рекомендуемой литературы Основная

1. Гаврилов, Г.П. Задачи и упражнения по дискретной математике/Г.П. Гаврилов, А.А. Сапоженко. – М.:Физматлит, 2005.

2. Гореленков, А.И. Теория вероятностей и математическая статистика: сб. задач/А.И. Гореленков, В.М. Кобзев, А.П. Мысютин. – Брянск, БГТУ, 2007.

3. Просветов, Г.И. Дискретная математика: задачи и решения: учеб.–практ. пособие/Г.И. Просветов. – М.: Альфа – Пресс, 2013.

4. Пугач, Л.И. Высшая математика. Задачи по дискретной математике, математической логике и теории алгоритмов: метод. указания к практическим занятиям для студентов I курса очной формы обучения по специальностям 220400 «Программное обеспечение», 220300 «Системы автоматизированного проектирования» и 075300 «Организация и технология защиты информации»/Л.И. Пугач. – Брянск: Изд-во БГТУ, 2005.

Дополнительная

5. Андреева, Т.В. Методические указания по курсу «Дискретная математика для социологов»/Т.В. Андреева. – М.: ГУ ВШЭ, 2007.

6. Мельников, О.И. Теория графов в занимательных задачах/О.И. Мельников. – 4-е изд. – М.: ЛИБРОКОМ, 2012.

7. Яблонский, С.В. Введение в дискретную математику/С.В. Яблонский. – М.: Высш.шк., 2008.