59

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Брянский государственный технический университет

УТВЕРЖДАЮ          

Ректор университета

__________О.Н. Федонин “____”___________2014 г.

ДИСКРЕТНАЯ МАТЕМАТИКА

Методические указания к выполнению

практических заданий и задачи для студентов

I курса очной формы обучения по направлениям подготовки

230400 «Информационные системы и технологии», 090900 «Информационная безопасность», 040100 «Социология», 090303 «Информационная безопасность автоматизированных систем»

I семестр

Брянск 2014

УДК 511

Дискретная математика [Текст]+[Электронный вариант]: методические указания к выполнению практических заданий и задачи для студентов I курса очной формы обучения по направлениям подготовки 230400 «Информационные системы и технологии», 090900 «Информационная безопасность», 040100 «Социология», 090303 «Информационная безопасность автоматизированных систем» II семестр. – Брянск, М.: БГТУ, 2014. – 60с.

Разработали: Андросенко В.А., ст.преп.

Сенько К.А., асс.                

Рекомендовано кафедрой «Высшая математика» БГТУ

(протокол № 4 от 19. 12. 13)

Научный редактор А.Г. Белоусов

Редактор издательства Л.И. Захарова

Компьютерный набор А.П. Левкина

Темплан 2014г., п.254

Подписано в печать Формат 60´84 1/16. Бумага офсетная. Офсетная печать. Усл. печ. л. 3,49 Уч.-изд. л. 3,49 Тираж 30 экз. Заказ Бесплатно ____________________________________________________________________

Издательство Брянского государственного технического университета

241035, г. Брянск, бульвар 50 лет Октября, 7, тел 58-82-49

Лаборатория оперативной полиграфии БГТУ.

Предисловие

Современная математика уже не такая, какой она была в начале XX века. В ней появилось большое количество новых дисциплин, широко применяющихся на практике. Например, дисциплины, объединенные под общим названием «Дискретная математика».

Дискретная математика является в настоящее время очень интенсивно развивающимся разделом математики. Это связано с повсеместным распространением кибернетических систем, языком описания которых она является. Кроме того, дискретная математика является теоретической базой информатики, которая все глубже и глубже проникает не только в науку и технику, но и в повседневную жизнь.

Предлагаемое пособие призвано познакомить студентов с важнейшими разделами дискретной математики, такими как:

1. Элементы теории множеств и комбинаторики.

2. Теория графов.

3. Булевы функции.

Каждый раздел – это отдельная тема, которая разбита на параграфы. В начале параграфа приводится необходимый минимум теоретических сведений, затем подробно разбираются модельные примеры. После каждого примера приводятся задачи для самостоятельного решения. Звездочкой обозначены задачи повышенной трудности, которые решаются на занятиях по усмотрению преподавателя или используются студентом дома для углубленной подготовки.

Тема 1. Элементы теории множеств и комбинаторики

§1. Понятие множества. Операции над множествами

Запись АВ означает, что множество А содержится в множестве В, т.е. является подмножеством.

Множество называется пустым и обозначается , если оно не содержит ни одного элемента.

Наглядно изображать множества принято в виде диаграмм Эйлера-Венна, на которых множества выглядят как плоские фигуры.

Объединением множеств А и В называется множество АВ, элементами которого являются все элементы множества А и все элементы множества В.

АВ={a: aA или аВ}

А В

Пересечением множеств А и В называется множество АВ, элементами которого являются все элементы, одновременно принадлежащие множеству А и множеству В.

АВ={a: aA и 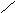аВ}.

А В

Разностью множеств А и В называется множество А\В, элементами которого являются все элементы множества А, не содержащиеся во множестве В.

А\ В={a: aA и 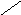аВ}.

А В

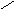
Симметрической разностью множеств А и В называется множество АВ=(А\ В)(В\А)

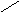
А В

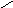
Часто складывается ситуация, когда все рассматриваемые множества содержатся в некотором едином множестве , называемом универсальным множеством. Дополнением множества А (до универсального) называется множество 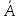=\А.

А

Примеры решения задач

Задача 1. Пусть А={1,2,3,4,5,6,7}; В={4,5,6,7,8,9,10}; С={2,4,6,8,10}; И={1,2,3,4,5,6,7,8,9,10}. Определить следующие множества: .

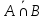Решение.

АВ={4,5,6,7}

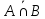={1,2,3,8,9,10}.

Задача 2. Для множества используйте диаграммы Эйлера-Венна и заштрихуйте те ее части, которые изображают заданное множество: (АВС)\ (АВС).

Решение.

1. 2)

А В

А В

С С

3)

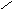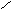А В

С

Задача 3. Доказать формулу А(ВС)=(АВ)(АС), пользуясь принципом "ХУ и УХХ=У".

Доказательство.

Пусть Х=А(ВС), У=(АВ)(АС).

1. Пусть аХ(аА(ВС)) (аА) и (а(ВС)) аА и (аВ или аС))(аА) и (аВ)) или ((аА) и (аС))  (а(АВ)) или (а(АС)) (а(АВ)  (АС))  аУХУ.

2. Пусть аУ(а(АВ)(АС)) (а(АВ)) или (а(АС)) (аА) и (аВ)) или (аА) и ((аС)(аА) и ((аВ) или (аС))  ((аА) или (а(ВС)) (аА(ВС)) аХУХ.

Из 1. и 2.  Х=У.