
- •Высшая математика
- •II курса очной формы обучения
- •Оглавление
- •Глава 1. Комплексные числа
- •1.1. Основные понятия
- •1.2. Операции над комплексными числами
- •Глава 2. Матрицы и операции над ними
- •2.1. Основные понятия
- •2.2. Операции над матрицами
- •2.3. Обратная матрица. Матричные уравнения и системы линейных уравнений
- •Решение систем линейных уравнений с помощью обратной матрицы
- •2.4. Собственные числа и собственные векторы матрицы
- •Глава 3. Дифференциальные уравнения
- •3.1. Понятия о дифференциальном уравнении
- •3.2. Уравнения с разделяющимися переменными
- •3.3. Линейные дифференциальные уравнения 1-го порядка
- •Глава 4. Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Глава 5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •Второго порядка с постоянными коэффициентами
- •5.2 Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •Глава 6. Линейные неоднородные
- •Метод вариации произвольных постоянных (метод Лагранжа)
- •Глава 7. Элементы операционного исчисления
- •7.1. Преобразование Лапласа. Оригинал и изображение
- •7.2. Решение задачи Коши для линейных дифференциальных уравнений
- •Глава 8. Интегрирование однородных систем с постоянными коэффициентами
- •Глава 9. Ряды
- •9.1. Числовые ряды с положительными членами
- •9.2. Знакочередующиеся ряды
- •9.3. Степенные ряды
- •9.4. Разложение функций в степенные ряды
- •9.5. Ряды Фурье
- •Список рекомендуемой литературы Основная
- •Дополнительная
Глава 6. Линейные неоднородные
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Линейные неоднородные дифференциальные уравнения
с постоянными коэффициентами и со специальной
правой частью
Пусть задано дифференциальное уравнение вида
![]() (6.1)
(6.1)
Общее решение Y неоднородного дифференциального уравнения (6.1) равно сумме общего решения уоо соответствующего однородного уравнения и какого-либо частного решения учн неоднородного уравнения:
Yон=уоо+учн (6.2)
Для специальных видов функции f(x), являющейся правой частью уравнения (6.1), yчн удается найти методом неопределенных коэффициентов. Составить частное решение для дифференциального уравнения этого типа может помочь следующая таблица:
Таблица 1.
|
f(x) |
Замечания |
Вид учн |
|
f(x)=Фn(x) – многочлен n-й степени |
Число 0 не является корнем характеристического уравнения |
учн=Qn(x) – полный многочлен n-й степени с неизвестными пока коэффициентами |
|
Число 0 является корнем характеристического уравнения кратности |
учн=Qn(x)х | |
|
f(x)=Фn(x)eax |
Число а не является корнем характеристического уравнения |
учн=Qn(x)eax |
|
Число а не является корнем характеристического уравнения кратности |
учн=Qn(x)eaxx | |
|
f(x)= eax (Фn(x)cosbx+ +Rm(x)sinbx) |
Числа аbi не являются корнями характеристичес-кого уравнения |
учн=eax (Qk(x)cosbx+ +Q1k(x)sinbx), k – наибольшая из степеней n и m; Qk(x), Q1k(x) – два разных многочлена одной и той же степени k |
|
Числа аbi являются корнями характеристичес-кого уравнения кратности . Замечание: Пара чисел аbi является корнем кратности 1 |
учн=eax (Qk(x)cosbx+ +Q1k(x)sinbx) x |
Если правая часть
уравнения (6.1) представляет собой сумму
двух функций, т.е. f(x)=f1(x)+f2(x),
то
 ,
где
,
где ,
, - частные решения уравнения от функций
f1(x)
и
f2(x)
соответственно.
- частные решения уравнения от функций
f1(x)
и
f2(x)
соответственно.
1. Найти частные решения неоднородных дифференциальных уравнений, если:
1.1 y"-3y'+2y=f(x); f(x) имеют вид:
а) 10е-х; б) 3е2х; в) 2sinx; г) 2х3-30; д) 2excos(x/2); е) х+1-е-2х; ж) ех(3-4х); з) 3х+5sin2x; и) 2ех-е-2х.
1.2. 2y"+5y'=f(x); f(x) имеют вид:
а) 5х2-2х-1; б) ех; в) 29cosx; г) 29xsinx; д)100хе-хcosx.
1.3. y"-4y'+4y=f(x); f(x) имеют вид:
а) 1; б) е-х; в) 3 е2х; г) 2(sin2x+x).
1.4. y"+y=f(x); если f(x) равны:
а) 2х3-х+2; б) -8cos3x; в) cosx; г) sinx-2e-x.
1.5. Записать вид частного решения для уравнения y"-2y'+10у=f(x), если f(x) имеют вид:
а) х2-4х; б) хех; в) (2х2-3)е3х; г) ехcos3x; д) хехsin3x; е) ех(xsin3x+x2cos3x).
2. Решить следующие дифференциальные уравнения:
а) y"-5y'+6y=13sin3x;
б) y"-3y'+2y=ех;
в) y"-2y'+y=х3;
г) y"+4y=xsin2x;
д) y"+8y'=8х.
е) y"-3y'=18х-10cosx.
3.Найти решения дифференциальных уравнений, удовлетворяющих заданным начальным условиям:
а) y"+y=2(1-х); у(0)=2; у'(0)=-2;
б) y"-6y'+9y=9х2-12х+2; у(0)=1; у'(0)=3;
в) y"+9y=36е3х; у(0)=2; у'(0)=6;
г) y"-4y'+4y=2е2х; у(0)=у'(0)=0;
д) y"+y=2cosx; у(0)=1; у'(0)=0;
е) y"+y=4xcosx; у(0)=0; у'(0)=1.
____________________
Ответы:
а)
 ;
б) 3хе2х;
в)
;
б) 3хе2х;
в)
 ;
г)
;
г) ;
д)
;
д) ;
е)
;
е)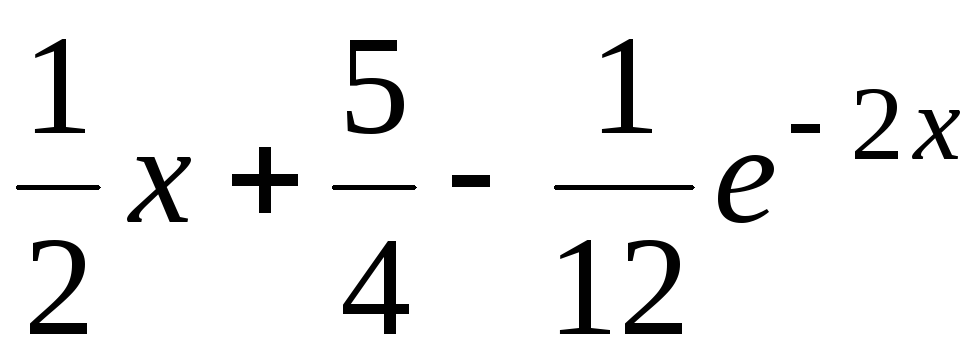 ;
ж)ех(2х2+х);
з)
;
ж)ех(2х2+х);
з) ;
и)
;
и) .
.а)
 ;
б) 1/7ех;
в) 5sinx-2cosx;
г)
;
б) 1/7ех;
в) 5sinx-2cosx;
г) ;д)
;д) ((650х+2650sinx-
-(3250x-400)cosx).
((650х+2650sinx-
-(3250x-400)cosx).а) 1/4; б)1/9ех; в)
 ;
г)
;
г) .
.а) 2х3-13х+2; б) cos3x; в)
 г)
г)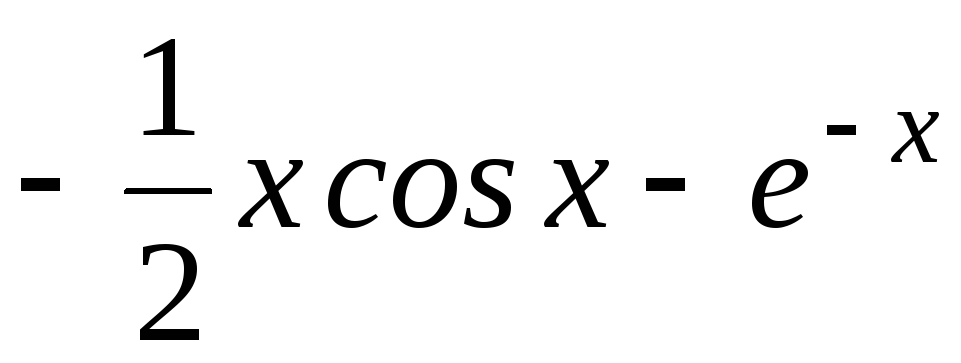 .
.а) Ах2+Вх+С; б) (Ах+В)ех; в) (Ах2+ВХ+С)е3х; г)ех(Аcos3x+ +Bsin3x)x; д) ех((Ах+В)sin3x+(Cx+D)cos3x)x; е)ех((Ах2+Вх+С) sin3x+(Dx2+Ex+F)cos3x)x.
а)
 ;
б)
;
б) ;в)
;в) +
+
+
+ +
+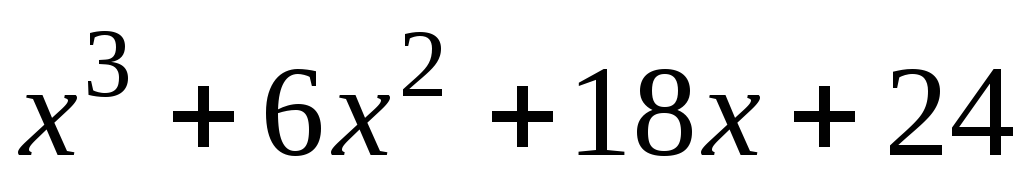 ;г)
;г) ;
;
д)
![]() ;
е)
;
е)![]() .
.
а) у=2-2х; б) у=х2+е3х; в) у=2е3х; г) у=х2е2х; д) у=cosx+xsinx; е)у=xcosx+x2sinx.
