
- •Высшая математика
- •II курса очной формы обучения
- •Оглавление
- •Глава 1. Комплексные числа
- •1.1. Основные понятия
- •1.2. Операции над комплексными числами
- •Глава 2. Матрицы и операции над ними
- •2.1. Основные понятия
- •2.2. Операции над матрицами
- •2.3. Обратная матрица. Матричные уравнения и системы линейных уравнений
- •Решение систем линейных уравнений с помощью обратной матрицы
- •2.4. Собственные числа и собственные векторы матрицы
- •Глава 3. Дифференциальные уравнения
- •3.1. Понятия о дифференциальном уравнении
- •3.2. Уравнения с разделяющимися переменными
- •3.3. Линейные дифференциальные уравнения 1-го порядка
- •Глава 4. Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Глава 5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •Второго порядка с постоянными коэффициентами
- •5.2 Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •Глава 6. Линейные неоднородные
- •Метод вариации произвольных постоянных (метод Лагранжа)
- •Глава 7. Элементы операционного исчисления
- •7.1. Преобразование Лапласа. Оригинал и изображение
- •7.2. Решение задачи Коши для линейных дифференциальных уравнений
- •Глава 8. Интегрирование однородных систем с постоянными коэффициентами
- •Глава 9. Ряды
- •9.1. Числовые ряды с положительными членами
- •9.2. Знакочередующиеся ряды
- •9.3. Степенные ряды
- •9.4. Разложение функций в степенные ряды
- •9.5. Ряды Фурье
- •Список рекомендуемой литературы Основная
- •Дополнительная
Глава 2. Матрицы и операции над ними
2.1. Основные понятия
Матрицей А размера mn называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений aij, называемых элементами матрицы, i=1,2,…,m, j=1,2,…,n.
Матрица А с элементами aij обозначается также (aij).
 .
.
Квадратной матрицей n-го порядка называется матрицей размера nn.
Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали (т.е. с индексами ij) равны нулю.
Единичной называется диагональная матрица с единицами на главной диагонали (обозначается Е).
Нулевой называется матрица, все элементы которой равны нулю.
Примеры матриц: а) квадратная; б) диагональная; в) единичная; г) нулевая:
а)
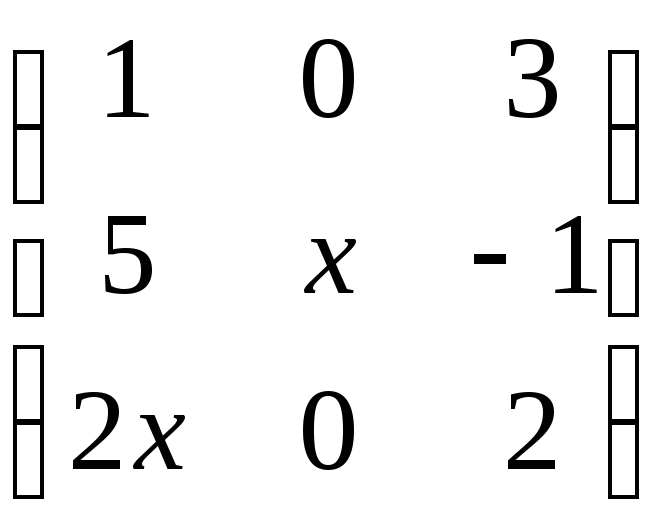 ;
б)
;
б)![]() ;
в)
;
в) ;
г)
;
г)![]() .
.
2.2. Операции над матрицами
Суммой матриц А = (aij) и В = (bij) одинакового размера называется матрица С = (сij) того же размера, причем сij= aij + bij, i,j.
Свойства операции сложения матриц
Для любых матриц А, В и С одного размера выполняются равенства:
А+В=В+А (коммутативность);
(А+В)+С=А+(В+С)=А+В+С (ассоциативность).
Произведением матрицы А = (aij) на число называется матрица В = (bij) того же размера, что и матрица А, причем bij= aij, i,j.
Свойства операции умножения матрицы на число
(А)=()А (ассоциативность);
(А+В)=А+В (дистрибутивность относительно сложения матриц);
(+)А=А+А (дистрибутивность относительно сложения чисел).
Произведением АВ
матриц А
и В
(размеров mn
и nr
соответственно) называется матрица С
размера mr,
такая, что сij=
ai1
b1j+
a12
b2j+…+
aik
bkj+…+
ain
bnj=![]() .
.
Таким образом, каждый элемент сij, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
Получение элемента сij схематично изображается так
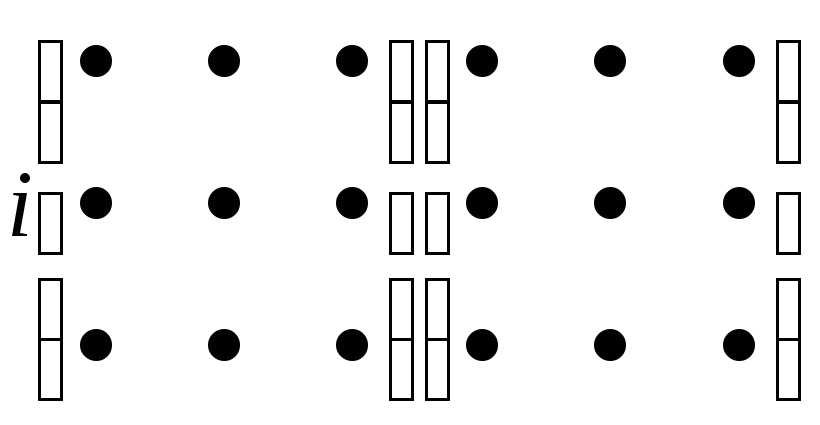

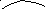

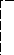
j
Произведение АВ существует, только если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц
(АВ)С=А(ВС)=АВС (ассоциативность);
(А+В)С=АС+ВС (дистрибутивность);
А(В+С)=АВ+АС (дистрибутивность);
АВВА (отсутствует коммутативность).
Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной (обозначается АТ).
_________________
1. Найти линейные комбинации заданных матриц:
а) А-Е,
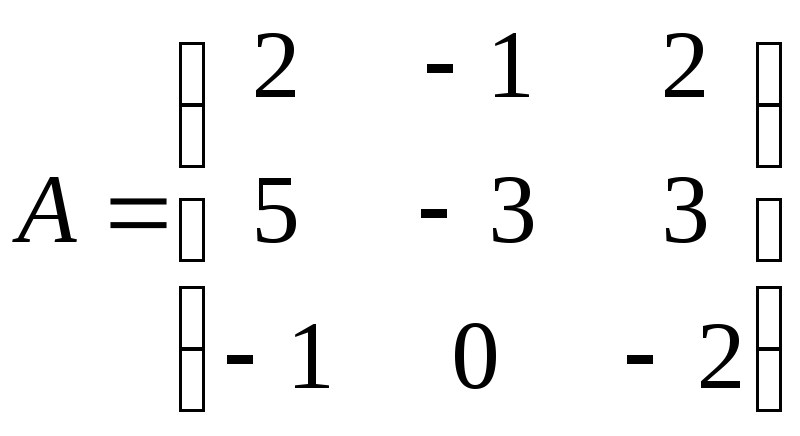 ;
;
б) 4А-5В,
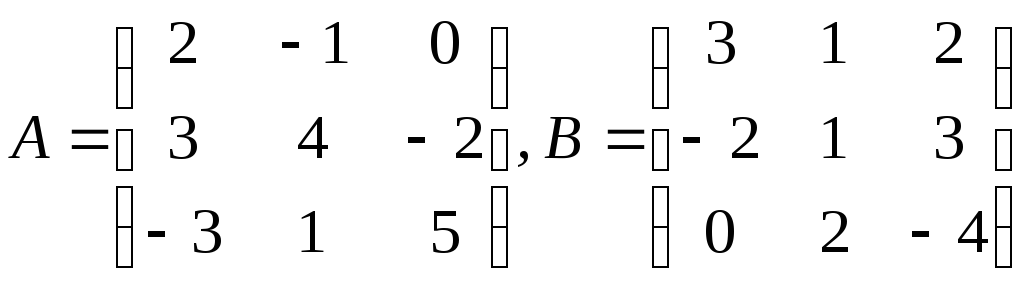 .
.
2. Найти произведения матриц АВ и ВА (если они существуют):
а)
![]() ;
б)А=(4
0 -2 3 1),
;
б)А=(4
0 -2 3 1),
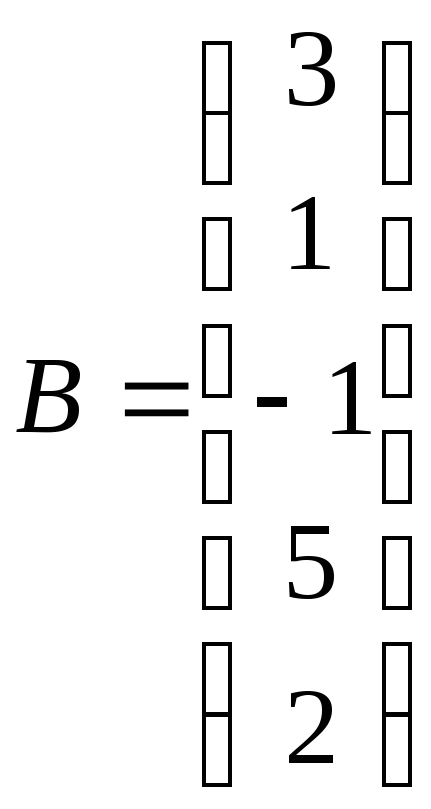 ;
;
в)
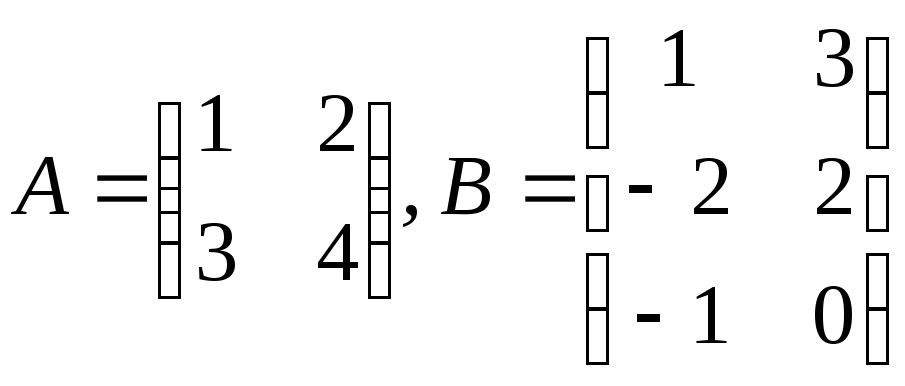 .
.
3. Проверить, коммутируют ли матрицы:
а)
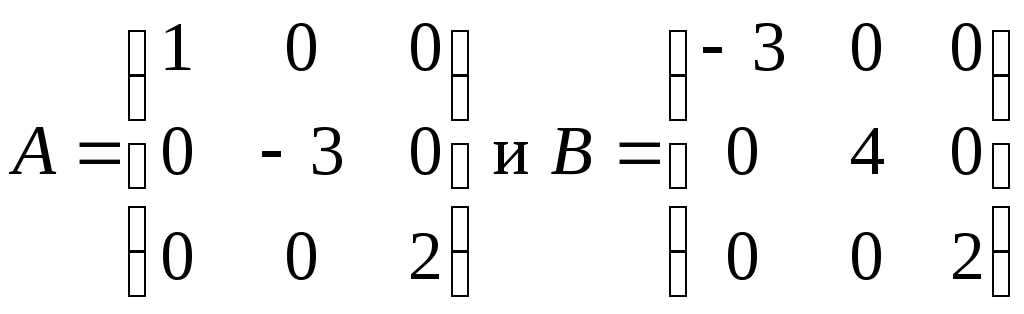 ;
;
б)
 .
.
4. Найти произведения матриц ААТ и АТА:
а)
![]() б)А=(1
2 3 4); в)
б)А=(1
2 3 4); в)
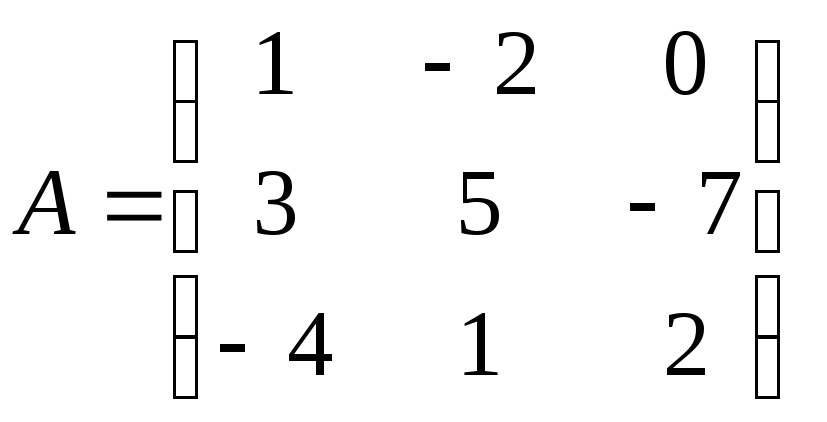 .
.
5. Найти линейные комбинации матриц:
а) 5А-3В+2С,
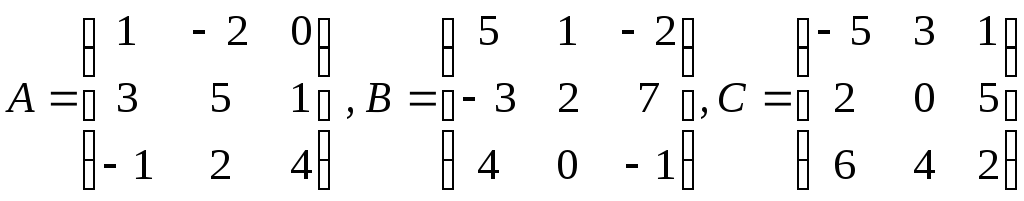 ;
;
б) А-Е,
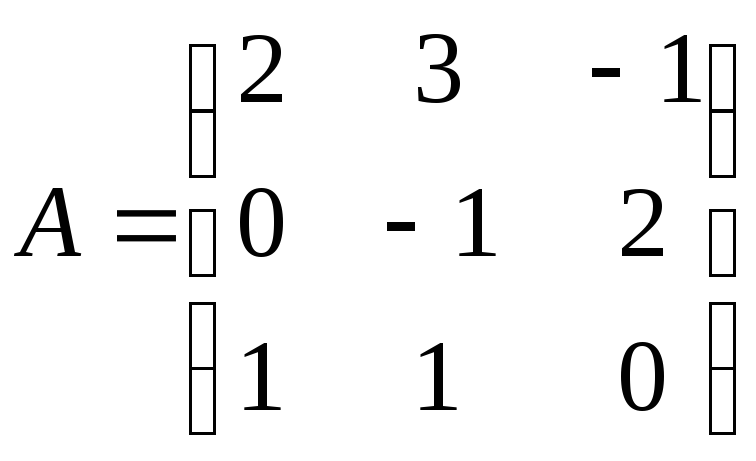 .
.
6. Найти произведения АВ и ВА (если это возможно):
а)
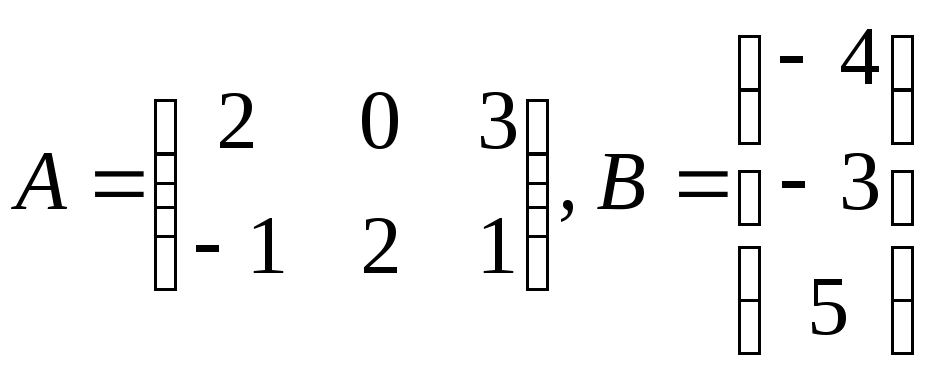 ;
б)
;
б)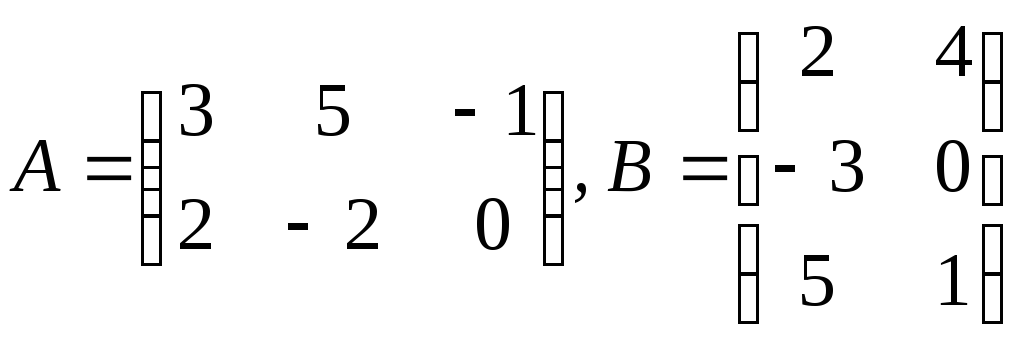 .
.
7. Найти произведения ААТ и АТА:
а)
 б)
б)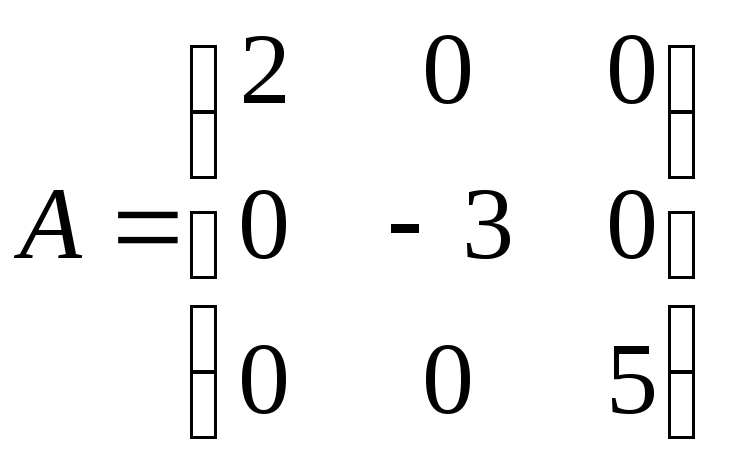 .
.
________________________
Ответы:
а)
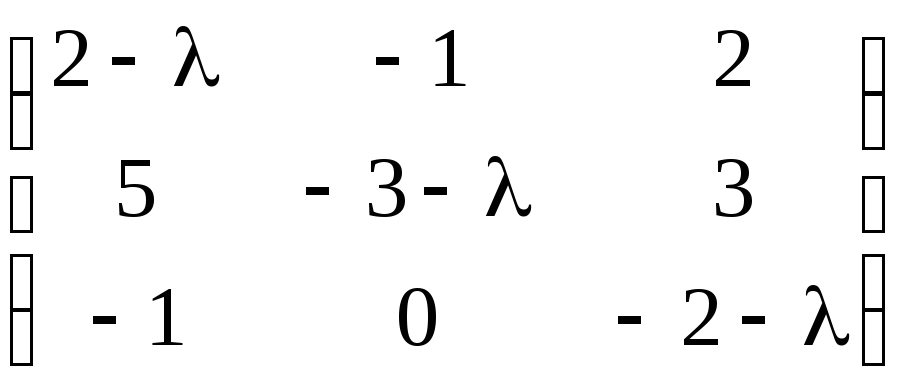 ;
б)
;
б) .
.а)
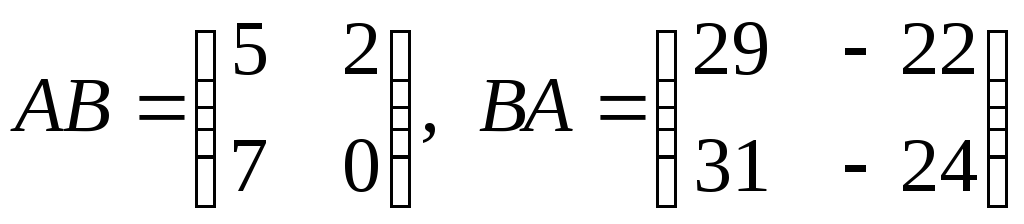 ;
;
б) АВ=(31);
 ;
;
в) АВ не существует,
 .
.
а) да; б) нет.
а)
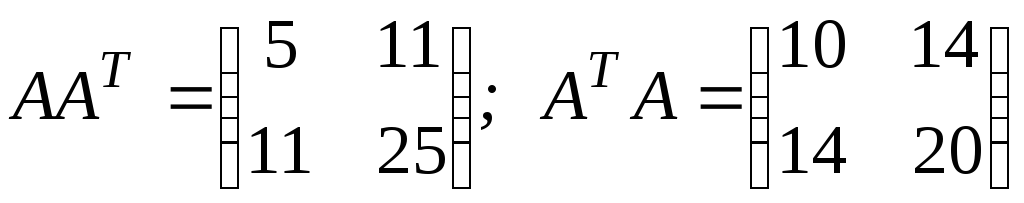 ;
;
б) ААТ=(30);
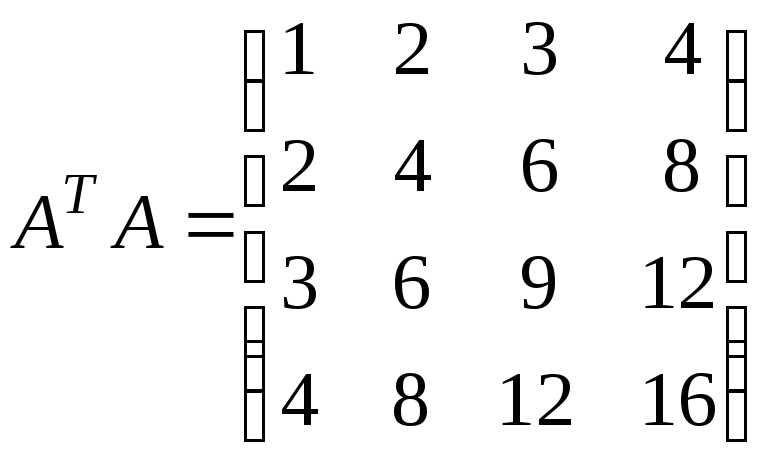 ;
;
в)
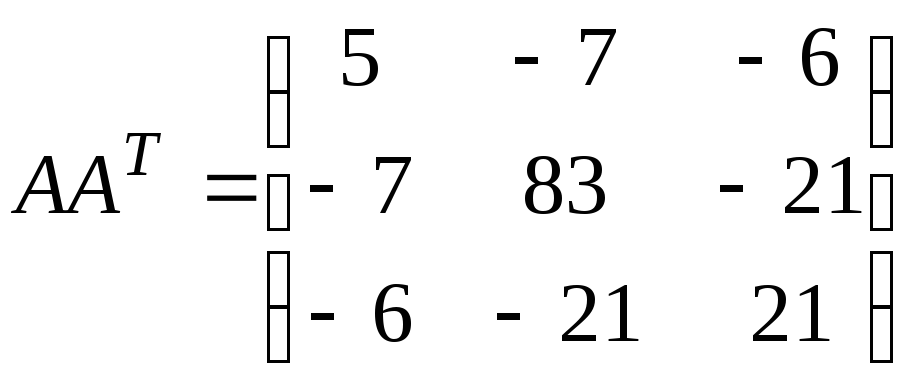 ;
;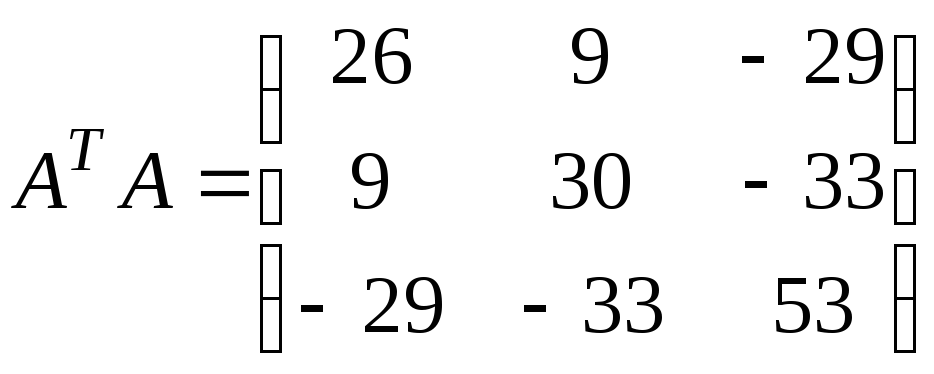 .
.
а)
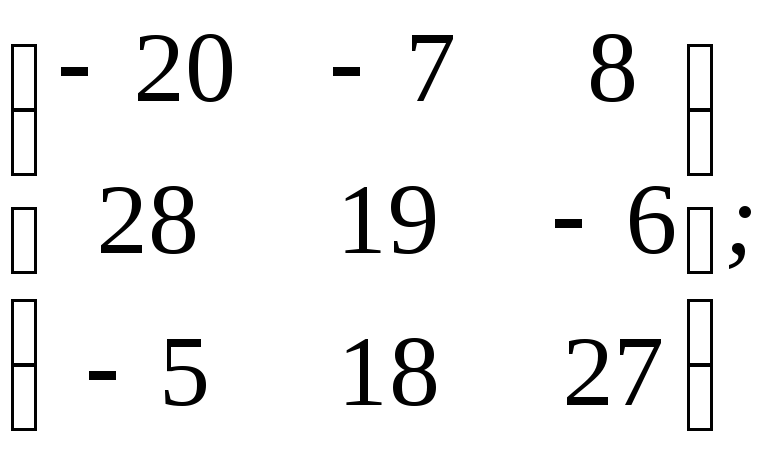 б)
б)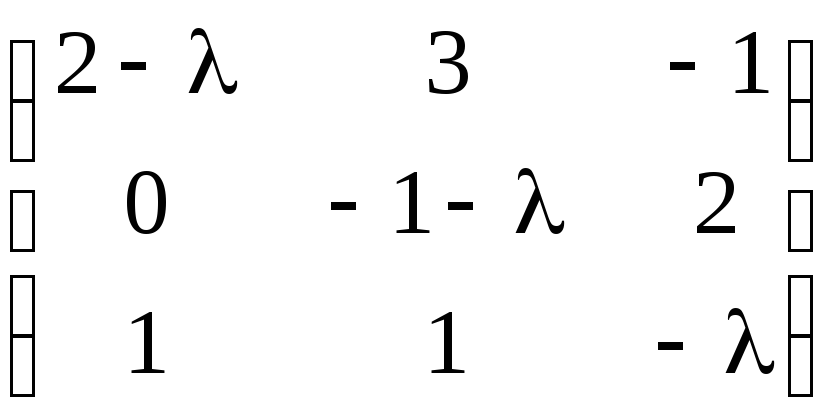 .
.а)
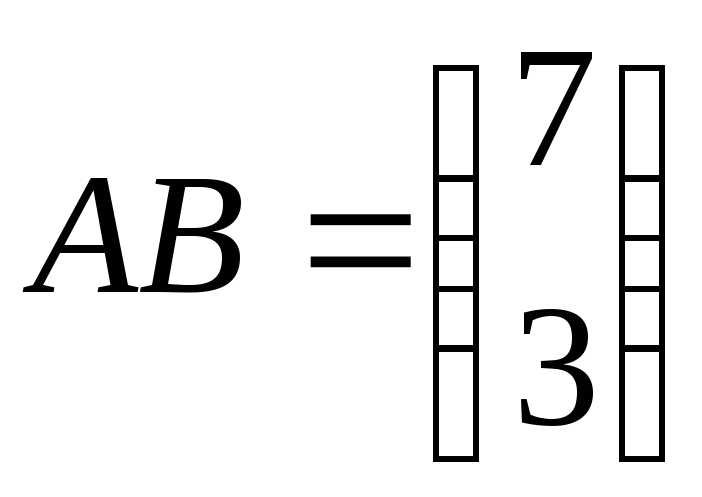 ,ВА
– не существует;
,ВА
– не существует;
б)
![]() ;
;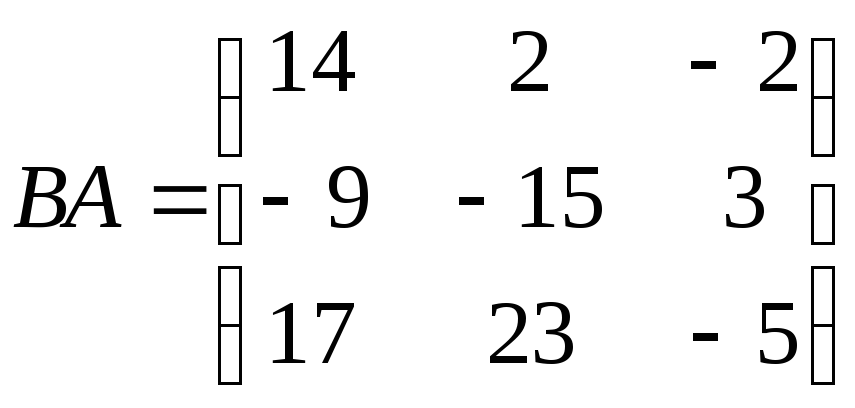 .
.
а)
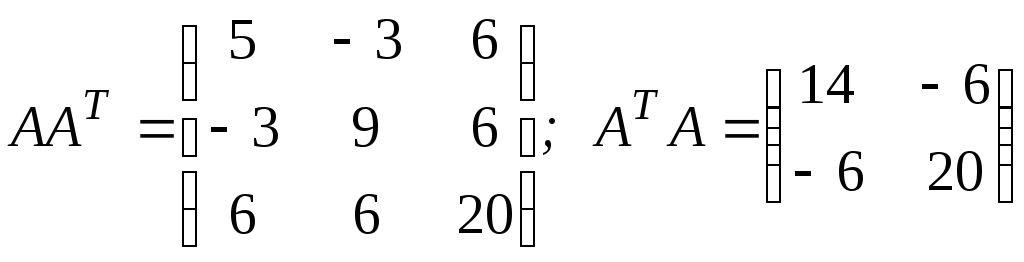 ;
;
б)
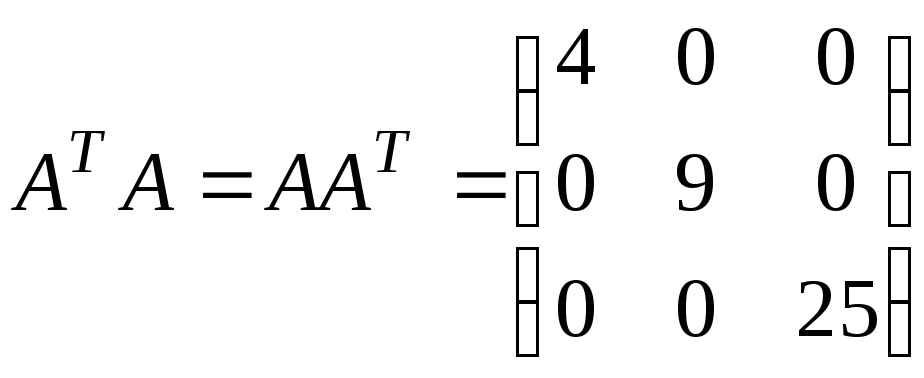 .
.
