Глава 1. Комплексные числа

1.1. Основные понятия

Комплексным числом z называется выражение вида z=x+iy, где х и у – действительные числа , i – мнимая единица, при этом i²= -1.

Число х – называется действительной частью комплексного числа и обозначается x=ReZ, а у – мнимой частью Z, y=ImZ.

Два комплексных числа z₁=x₁+iy₁ и z₂=x₂+iy₂ называются равными тогда и только тогда, когда равны их действительные части и равны их мнимые части: z₁= z₂, если x₁= x₂ и y₁= y₂.

Два комплексных числа z=x+iy и =x-iy, отличающиеся лишь знаком мнимой части, называются сопряженными.

Любое комплексное числоz=x+iy можно изобразить точкой на плоскости ХОУ и любой точке плоскости можно поставить в соответствие какое-то комплексное число. При этом x=ReZ, y=ImZ, сама плоскость ХОУ называется комплексной.

Комплексное число z=x+iy можно задать иначе, определив длину радиуса-вектора точки М, получившую название модуля комплексного числа, и величину угла между положительным направлением оси ОХ и радиусом-вектором. Этот угол (рис.1) называется аргументом комплексного числа, который обозначается как argZ.

Запись комплексного числа в виде z=x+iy называется алгебраической формой комплексного числа. Тригонометрическая форма определяет число z через его модуль и аргумент и имеет вид z=r(cos+isin), где , - аргумент комплексного числа; . При определении аргумента необходимо учитывать четверть комплексной плоскости, в которой лежит точка, соответствующая данному комплексному числу:

Вид числа z=re^i называется показательной формой комплексного числа.

1.2. Операции над комплексными числами

Пусть даны два комплексных числа в алгебраической форме: z₁=x₁+y₁i и z₂=x₂+y₂i. Тогда

z₁  z₂=(x₁ x₂)+(y₁y₂)i;

z₁z₂=( x₁+y₁i)( x₂+y₂i)= x₁x₂+ x₂ у₁i+ x₁ у₂i+ у₁y₂i² =( x₁x₂- у₁y₂)+i(x₂ у₁+ + x₁ у₂);

Если комплексные числа заданы в тригонометрической форме как z₁=r₁(cos₁+isin₁) и z₂=r₂(cos₂+isin₂),

то z₁z₂= r₁r₂(cos(₁+₂)+isin(₁+₂);

.

Формулы Муавра для возведения комплексных чисел в натуральную степень и извлечения корня n-й степени из комплексных чисел имеют вид:

(x+yi)ⁿ=(r(cos+isin))ⁿ=rⁿ(cosn+isinn);

где k=0,1,2,…,n-1.

________________

1. Выполнить действия над комплексными числами:

а) (2+3i)(3-2i); б) (a+bi)(a-bi); в) (3-2i)²; г) (1+i)³; д) ; e).

2. Найти , если z₁=3+5i; z₂=2+3i; z₃=1+2i.

3. Заданы комплексные числа: а) 1; б) i; в) -1; г) –i; д) 23-2i; е) 3+i; ж) 1+i3. Изобразить эти числа векторами на комплексной плоскости и записать их в тригонометрической и показательной формах.

4. Вычислить по формуле Муавра:

а) ; б) (-1+i)⁵; в) (1-i3)⁶.

5. Найти: а) ; б); в); г). Найденные значения изобразить точками на комплексной плоскости.

6. Решить уравнения на множестве комплексных чисел:

а) х³+8=0; б) х⁴+4=0; в) х⁵+32i=0; г) х³=42(1+i).

__________________

7. Выполнить действия над комплексными числами:

а)(1+i)(5-2i); б) 1+i³-; в) ; г).

8. Записать в тригонометрической форме числа: а) 3i; б) -1-3i; в) 2-2i Изобразить эти числа на комплексной плоскости.

9. Вычислить: а) (2+3i)³; б) (cos2+isin2)⁴⁵; в) (-2+2i)⁶; г) (1+ i3)⁹.

10. Найти значения: а) ; б); в).

11. Решить уравнения: а) х²+i=0; б) х⁴-16=0; в) х⁶-4х³+8=0. В задании в) ответ записать в показательной форме.

____________________

Ответы:

1. а) 12+5i; б) a²+b²; в) 5-12i; г) -2-2i; д) i; е)1+i.

2. .

3. а)1(cos0+isin0)=1e⁰ⁱ; б); в)1(cos+isin)= =1e^i; г); д); е) ; ж).

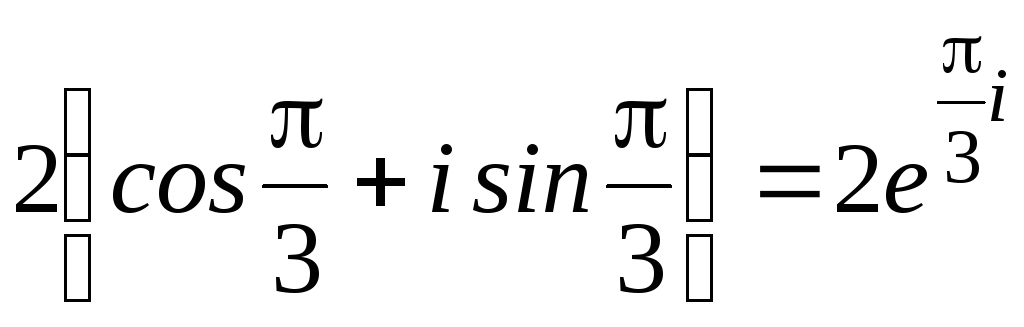4. а) 1; б) 4(1-i); в) 64.

5. а) 1; ; б) –i; ; в) 1+i; -1,36+0,365i; 0,365-1,36i; г) .

6. а) -2; 1; б)1i; в) ,k=0;1,…4; г) , k=0;1,2.

7. а) (5+2)+(5-2)i; б) 1; в) ; г)0.

8. а) ; б); в).

9. а) -46+9i; б) i; в) 512i; г) .

10. а) , k=0;1,2,3;

б) , k=0;…,4;

в) , k=0;…,5.

11. а) ; б)2; 2i; в) .