8. Полярные координаты. Вычисление площадей в полярных координатах

1. Сведения из теории

На плоскости задана полярная система координат, если выбраны 1) точка , называемаяполюсом, 2) луч , выходящий из точкии называемыйполярной осью (рис.11а).

Полярными координатами точки называются числа:полярный радиус иполярный угол  угол, на который надо повернуть полярную ось для того, чтобы её направление совпало с направлением вектора (рис.11а).

Если на плоскости задана прямоугольная декартова система координат , тосвязанная с ней полярная система координат выбирается так, чтобы полярная ось совпала с положительной полуосью(рис. 11б). Тогда выражение декартовых координат точки через её полярные координаты имеет вид:

, ,

а выражение полярных координат через декартовы координаты

, ,

Площадь фигуры , ограниченной непрерывной кривой, имеющей в полярных координатах уравнение,и лучами,(рис.12) находится по формуле

.

2. Примеры решения задач

   1. Построить кривую, заданную в полярных координатах уравнением (кардиоида). Найти площадь фигуры, ею ограниченной.

◄ 1) Построение кардиоиды. Построим сначала дугу кардиоиды, соответствующую значениям . Так как функцияна отрезкеубывает отдо, а на отрезкевозрастает отдо, то изображающая точка двигается по лучу, вращающемуся вокруг полюса ( угол поворота), приближаясь к полюсу, когда меняется отдо, и, удаляясь от него, когдаменяется отдо( расстояние до полюса). Для более точного построения отметим положение изображающей точки на лучах ,, найдя предварительно соответствующие значения полярного радиуса(табл.3), и соединим полученные точки плавной линией (рис.13).

Таблица 3

	0
	2		1		0		1		2

Так как функция имеет период, то вся кардиоида получается из построенной дуги поворотами на углы,, и, следовательно, совпадает с этой дугой.

2) Вычисление площади. Фигура , заштрихованная нарис.13, ограниченна дугой и лучами,. Согласно формуле (5.3) её площадь

.

В силу симметрии кардиоиды площадь фигуры, ею ограниченной

. ►

2. Построить кривую, задаваемую в полярных координатах уравнением ,(трехлепестковая роза). Найти площадь фигуры, ею ограниченной.

◄1) Построение кривой. Функция имеет период. Поэтому достаточно построить часть кривой, соответствующую. Вся кривая получится из нее поворотами на углы,. На отрезкефункциявозрастает отдо, а на отрезкеона убывает отдо(см.рис.14 графика этой функции). Поэтому дуга ,, имеет вид, изображенный нарис.15 жирной линией.

При , и так как полярный радиус, то на кривой нет точек с полярным углом.

Теперь, поворачивая построенную часть кривой на углы ,, получим кривую, состоящую из трех “лепестков”(рис.15).

2) Вычисление площади. Площадь фигуры , ограниченной дугой,,

.

Площадь фигуры , ограниченной всей кривой

. ►

3. Найти площади фигур, ограниченных линиями

, .

◄ Уравнение равносильно уравнениюи потому задает окружность радиусас центром в точке (1,0). Уравнениезадает прямую, проходящую через начало координат. Фигурыи, которые они ограничивают, изображены нарис.16.

Перейдем в уравнениях к полярным координатам. По формулам получаем

или ;

, ,,.

Поэтому фигура ограниченна дугой,и лучами,. Её площадь

.

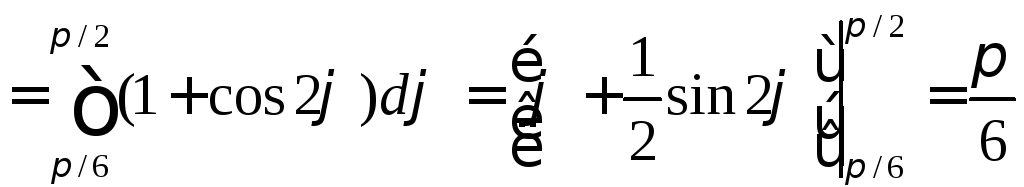Площадь фигуры :. ►

4. Кривая задана в полярных координатах уравнением . Записать уравнения кривой в декартовых координатах.

◄ По формулам получаем

.►

3. Задачи для самостоятельного решения

   1. Изобразить кривые, заданные в полярных координатах уравнениями а) 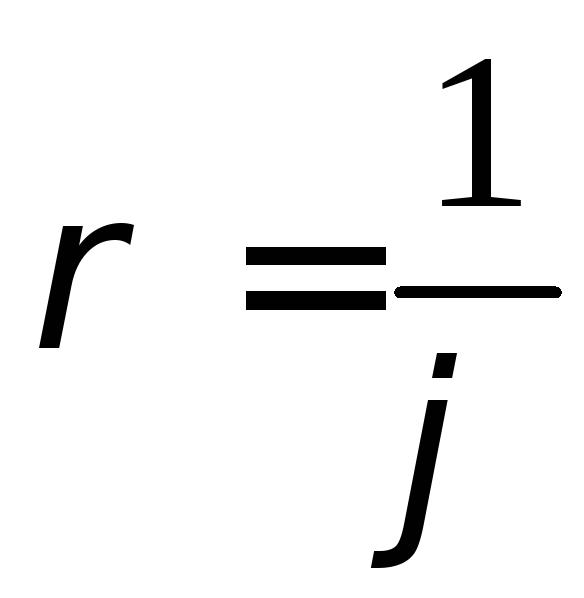, б).

   2. Точки изаданы декартовыми координатами. Найти их полярные координаты для случаев а),; б) ,.

В задачах 5.3.2-5.3.6 найти площади фигур, ограниченных указанными кривыми.

3. Дугой логарифмической спирали ,,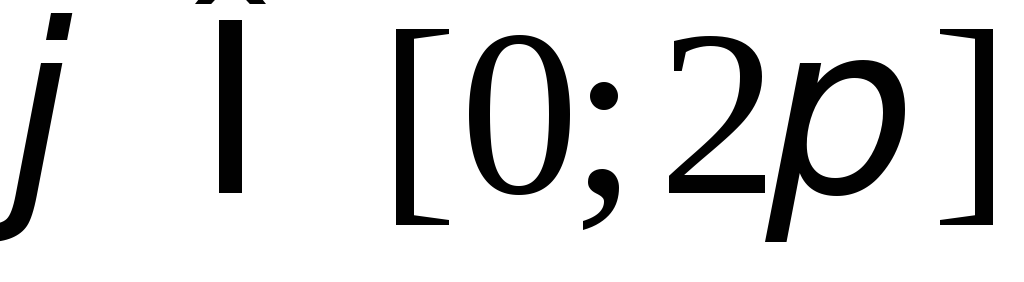 и лучом.

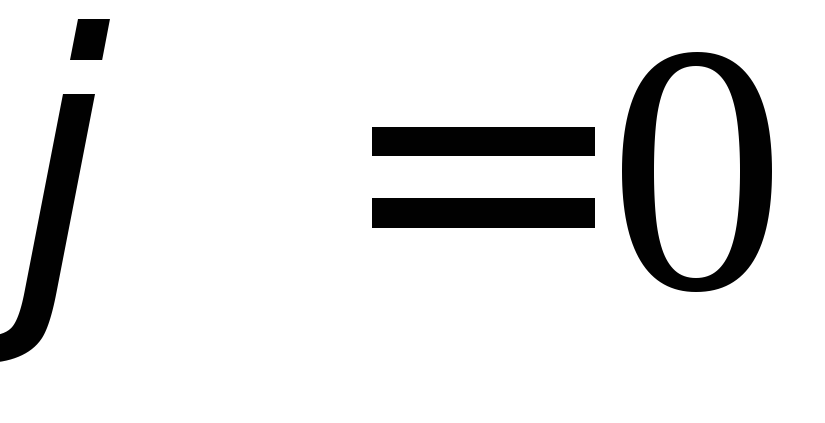4. Кардиоидой ,.

5. Лемнискатой Бернулли ,.

6. , .

7. , .