8. Формула Ньютона-Лейбница. Интегрирование по частям в определенном интеграле. Замена переменной в определенном интеграле

1. Сведения из теории

Если известна первообразная для функциина отрезке, то определенный интеграл отпо отрезкуможно вычислить поформуле Ньютона-Лейбница

.

Формула интегрирования по частям в определенном интеграле:

,

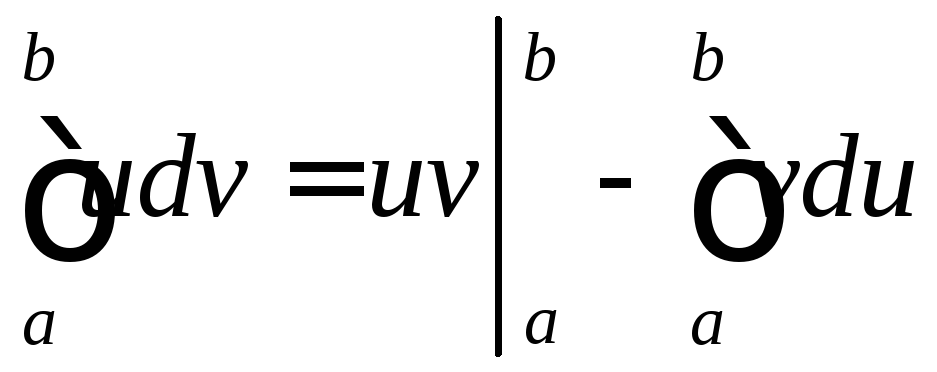где ,– функции, имеющие нанепрерывные производные, а,.

Формула замены переменной в определенном интеграле:

,

где – непрерывная функция,– монотонная функция, имеющая непрерывную производную, а,.

2. Примеры решения задач

1. Вычислить .

◄ Используем формулу Ньютона-Лейбница :

. ►

2. Вычислить .

◄ .

Замечание. Для инженера ответ, полученный в такой форме, обычно не является окончательным. Его следует записать в виде десятичной дроби с нужным числом знаков. Например, в рассматриваемом случае, получаем 1,07 с точностью . ►

3. Вычислить .

◄ Применим метод интегрирования по частям – формулу .

. ►

4. Вычислить .

◄ Сделаем замену переменной – обозначим . Тогда,. Найдем пределы интегрирования по новой переменной: приимеем, приимеем. По формуле

.►

5. Вычислить , если.

◄ Сначала вычислим интеграл по формуле Ньютона-Лейбница: . Теперь. ►

Замечание. Интегралы в примерах 2.2.1–2.2.4 – конкретные числа и их можно вычислить приближенно с любой точностью, не используя формулы Ньютона-Лейбница. В примере 2.2.5 интеграл зависит от параметраи его приближенное вычисление возможно только при конкретных числовых значениях, поэтому без формулы Ньютона-Лейбница обойтись нельзя.

6. Вычислить .

◄ Сделаем замену переменной – обозначим . Тогда,. Найдем пределы интегрирования по новой переменной: приимеем, приимеем.

По формуле

.►

3. Задачи для самостоятельного решения

Вычислить интегралы:

.	.
.	.
.	.
.	.
.	.
.	.
.	.

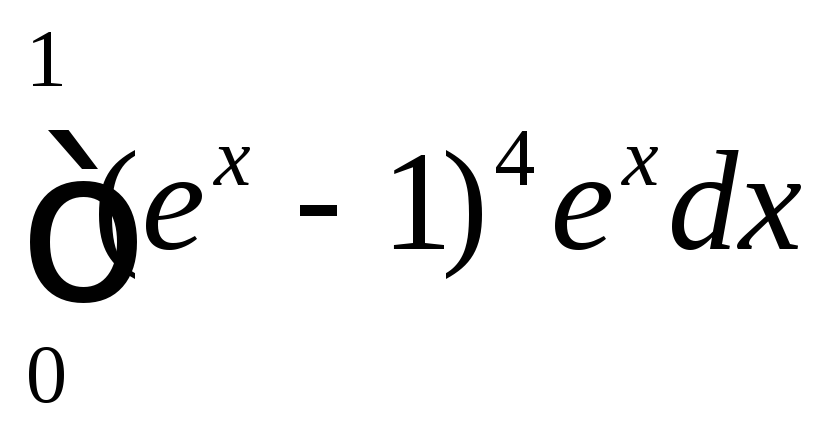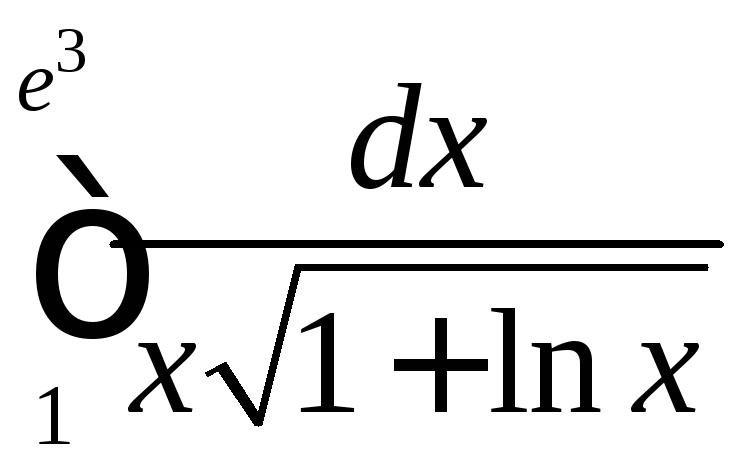8. Свойства определенного интеграла

1. Сведения из теории

1. Линейность интеграла.

,

.

2. Аддитивность интеграла.

.

3. Интегрирование неравенств.

Если , то.

4. Оценка модуля интеграла.

().

5. Среднее значение функции. Теорема о среднем.

Число

находится между нижней и верхней гранью функции на отрезке. Это число называетсясредним значением функции на отрезке . Интегральнаятеорема о среднем: если непрерывная функция на отрезке , то существует точка, в которой значение функции совпадает с ее средним: , или в подробной записи

.

6. Перестановка местами верхнего и нижнего пределов интегрирования меняет знак интеграла:

.

7. Производная интеграла как функции верхнего предела.

Если , то.

8. Интеграл от четной и нечетной функции по симметричному отрезку.

Если – нечетная функция на отрезке , то.

Если – четная функция на отрезке , то.

9. Интеграл от периодической функции по отрезку длины периода.

Если –периодическая функция периода , то

.