3. Задачи для самостоятельного решения

.

Вычислить интегралы, применяя указанные подстановки.

().	().
().	().

2. Интегрирование по частям

1. Сведения из теории

Если и– функции, имеющие непрерывные производные, то справедливаформула интегрирования по частям

,

или в краткой записи

.

2. Примеры решения задач

1. Вычислить

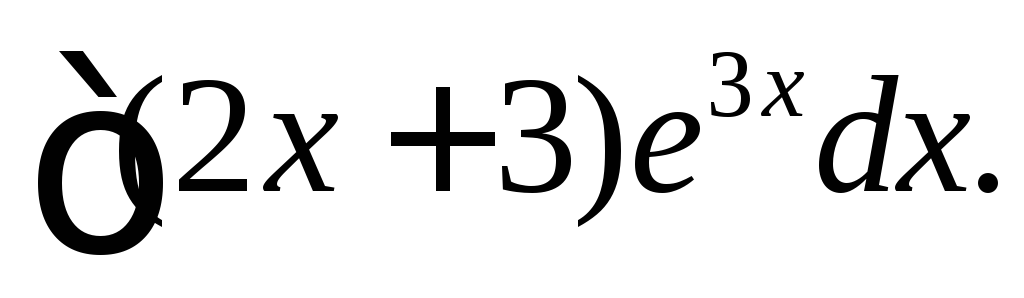
◄ Положим . Тогда(постояннуюC здесь считаем равной 0). По формуле интегрирования по частям имеем:

. ►

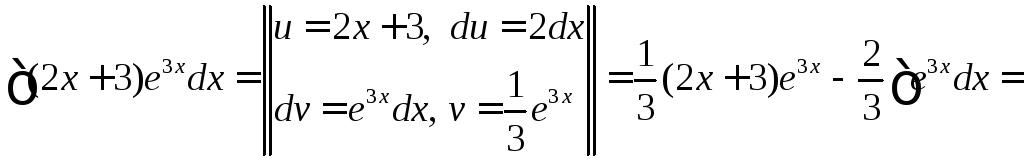
2. Вычислить .

◄

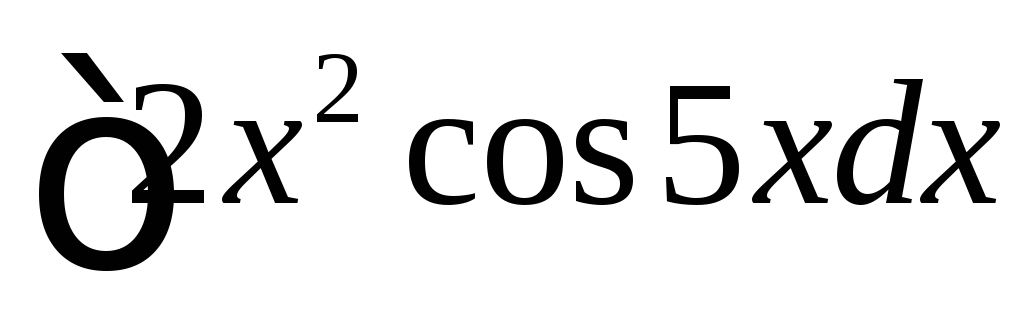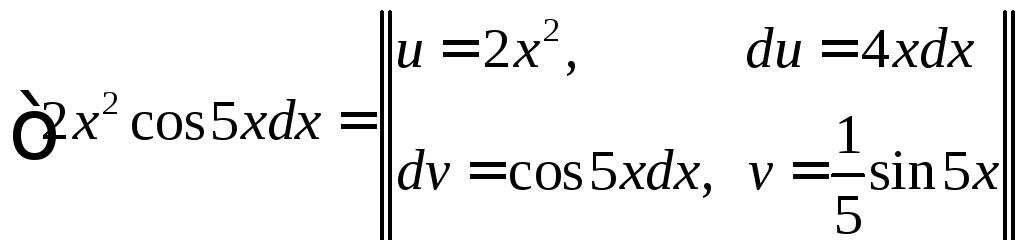
К стоящему справа интегралу снова применим формулу интегрирования по частям.

.►

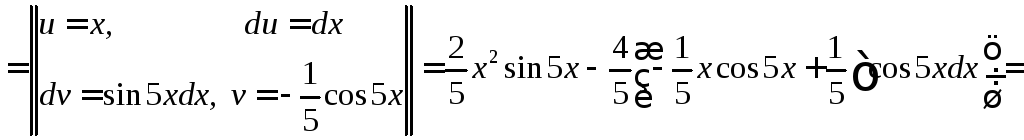
3. Вычислить .

◄

. ►

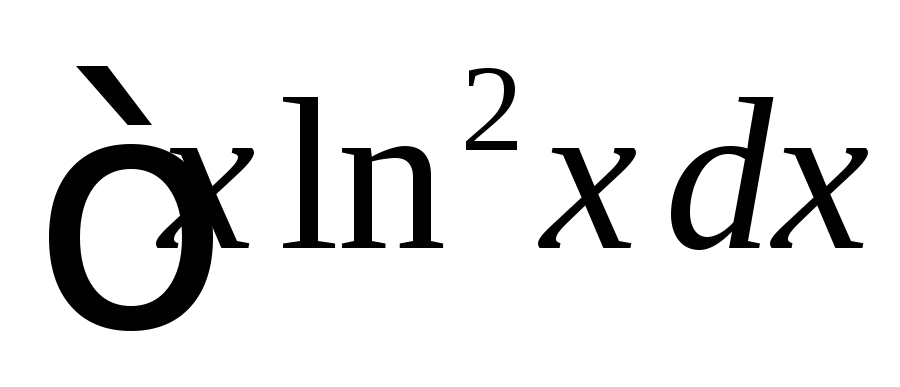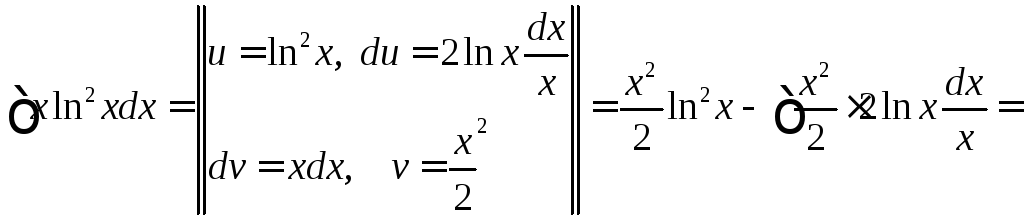
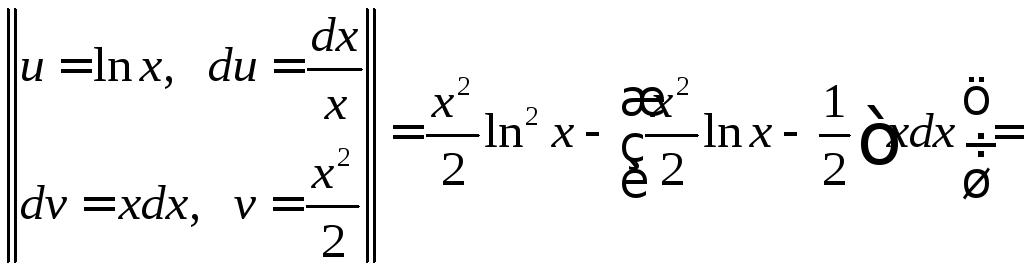
4. Вычислить .

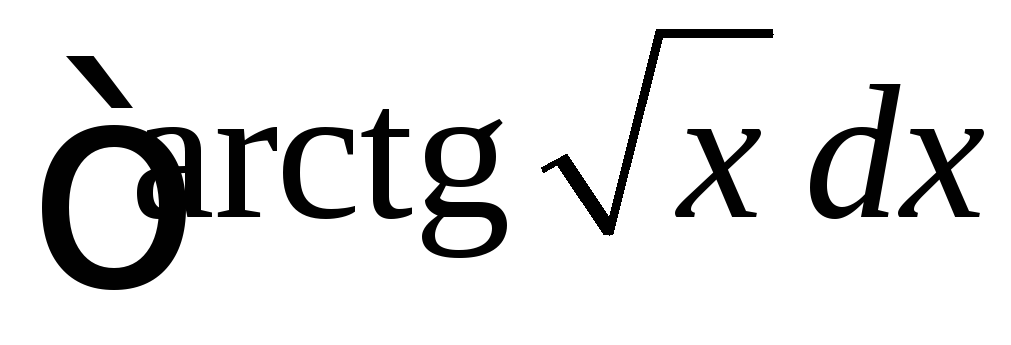◄ Сначала выполним замену переменной , а затем проинтегрируем по частям.

. ►

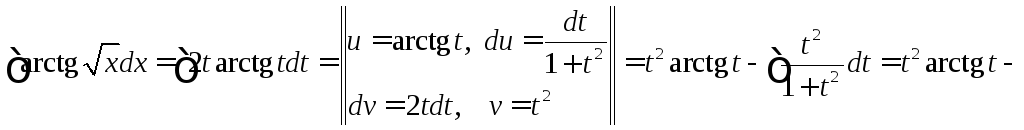
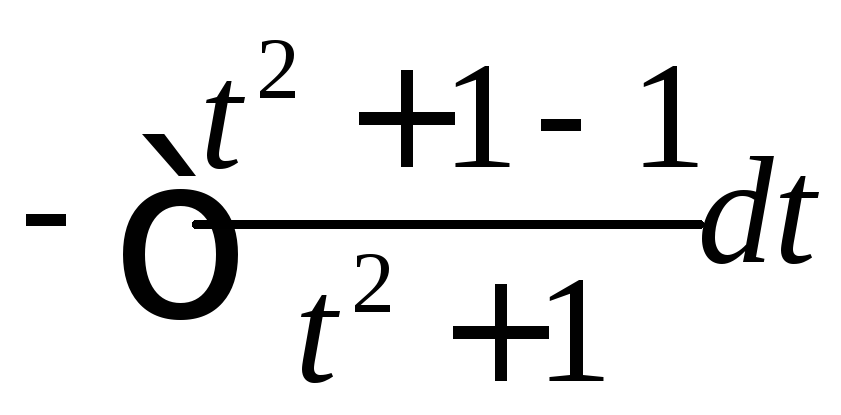
5. Вычислить .

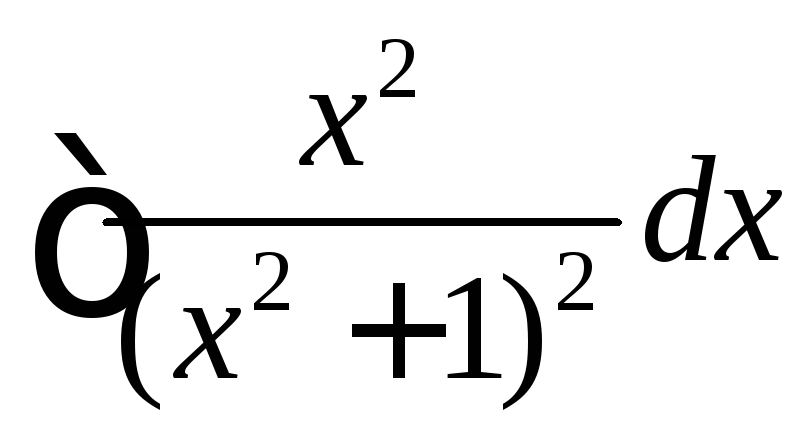◄ По формуле интегрирования по частям имеем:

. ►

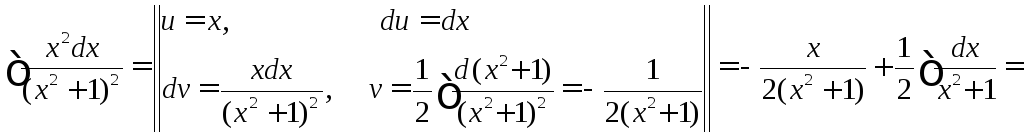
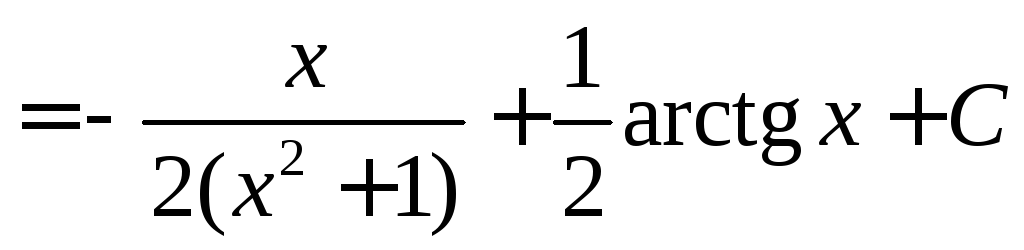6. Вычислить .

◄

.

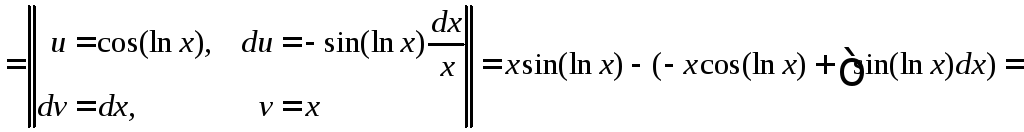
Из этого соотношения получаем

и, окончательно,

. ►

3. Задачи для самостоятельного решения

Найти интегралы методом интегрирования по частям.

	.
.
.
.	(замена ).

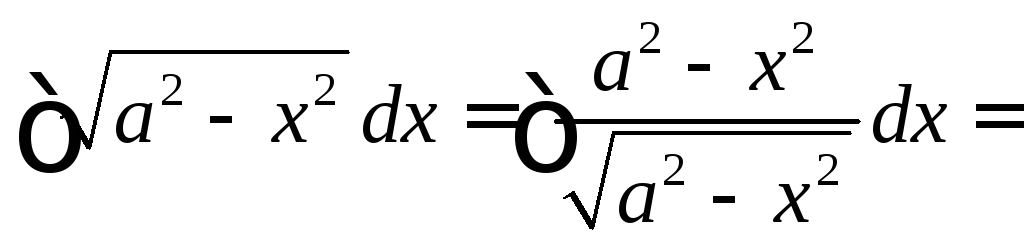
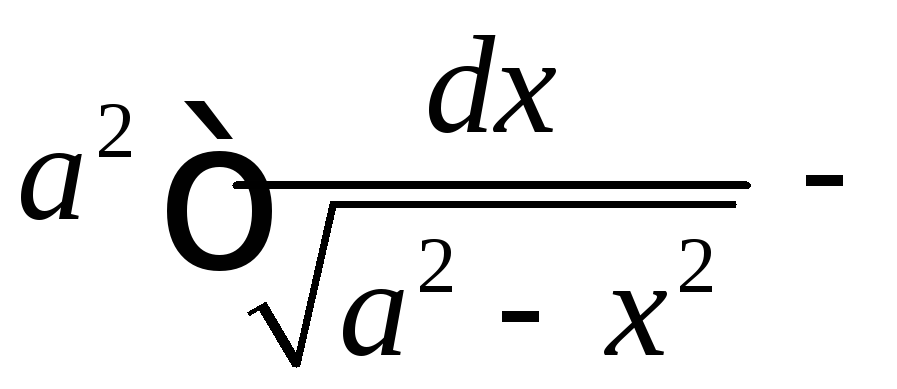
19. Вывести формулу 16 таблицы интегралов, используя преобразование 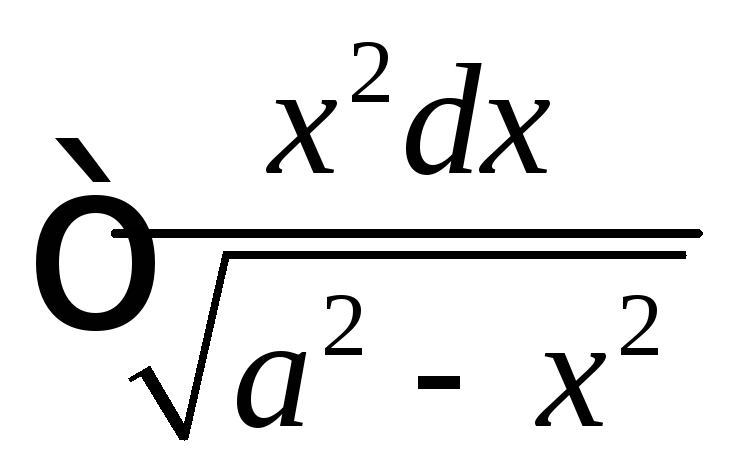и интегрирование по частям.

20. Вывести формулы 17 и 18 таблицы интегралов.

3. Простейшие интегралы,

СОДЕРЖАЩИЕ КВАДРАТНЫЙ ТРЕХЧЛЕН

1. Сведения из теории

Для вычисления интегралов вида

и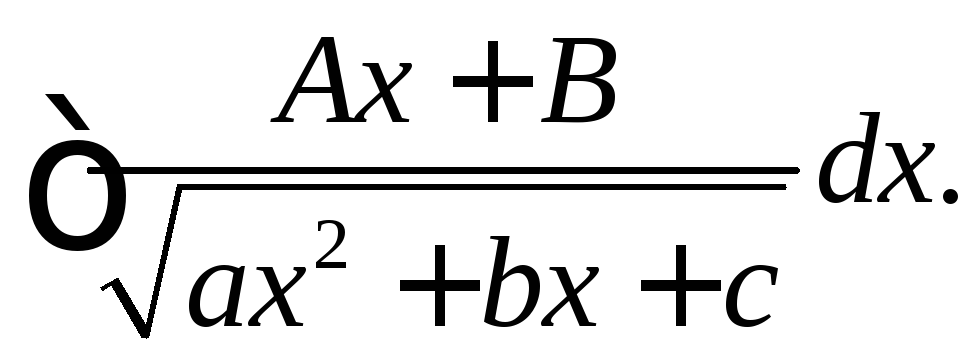

из квадратного трехчлена выделяется полный квадрат

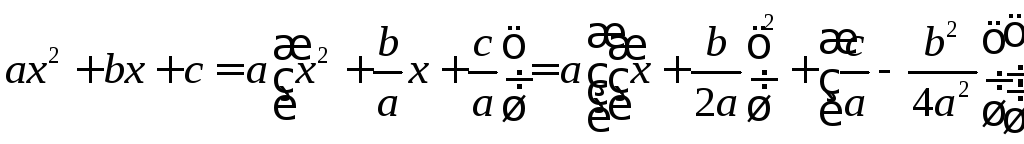
и делается замена переменных .

2. Примеры решения задач

1. Вычислить .

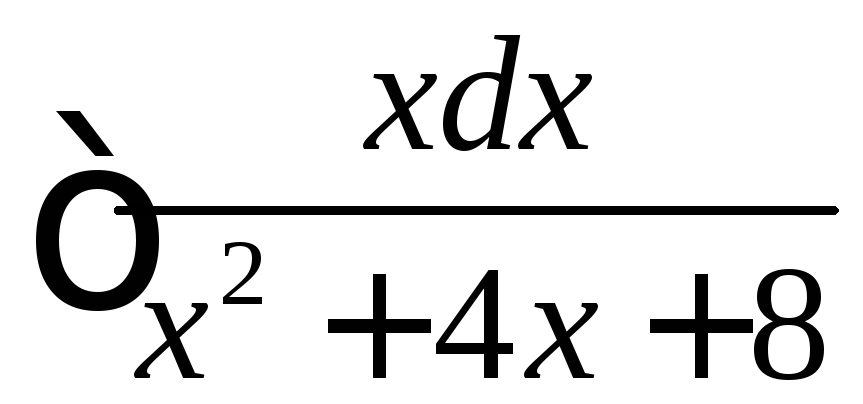◄ Выделим полный квадрат в квадратном трёхчлене:

.

Сделаем в интеграле подстановку . Тогда,,

=

(используем табличные интегралы 2 и 10)

=. ►

2. Вычислить .

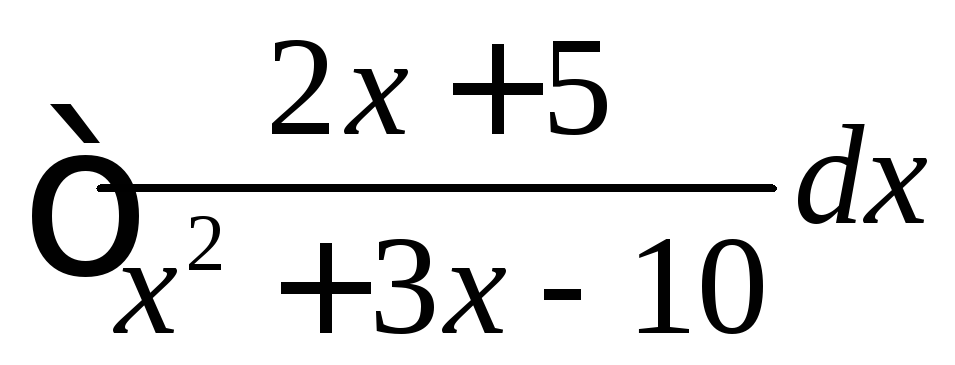◄ Выделим полный квадрат в квадратном трёхчлене

►

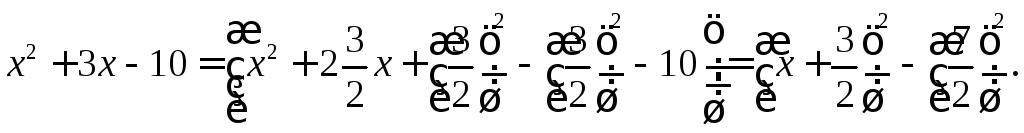
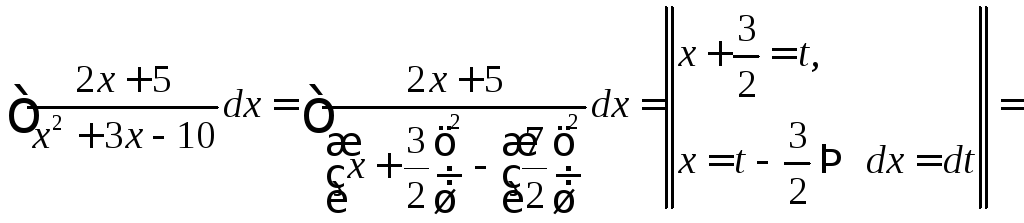
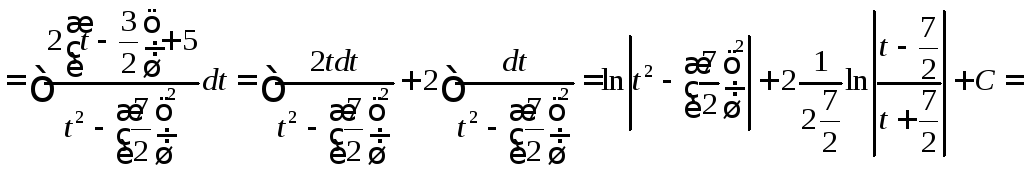
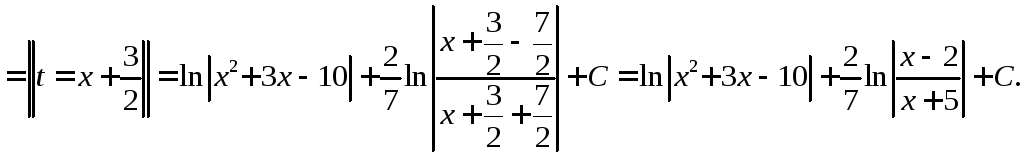3. Вычислить .

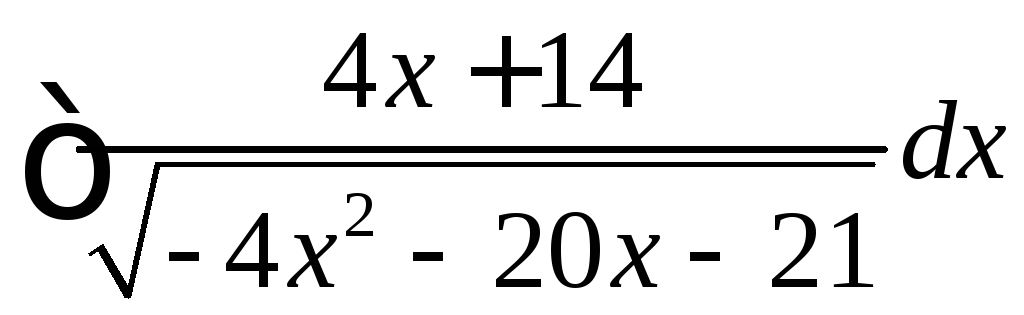◄ Выделим полный квадрат в подкоренном выражении:

.

. ►

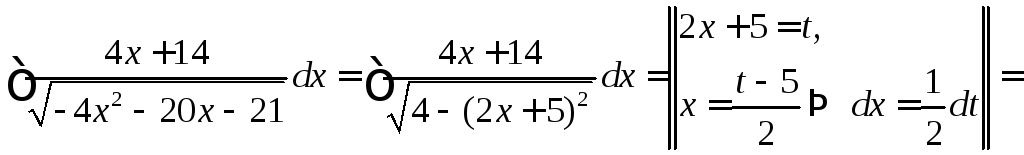
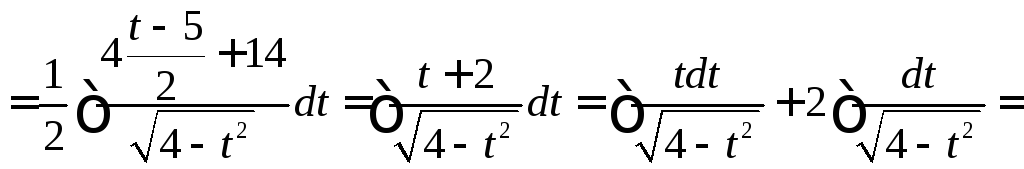
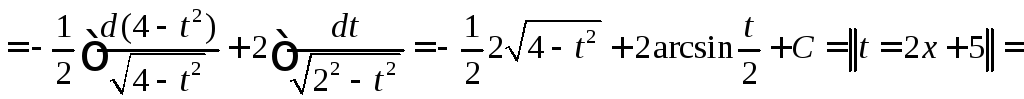
3. Задачи для самостоятельного решения

Вычислить интегралы, содержащие квадратный трёхчлен.

.	.
.	.
.	.
.
.

3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ

1. Основные понятия

Рациональной дробью (рациональной функцией) называется отношение многочленов

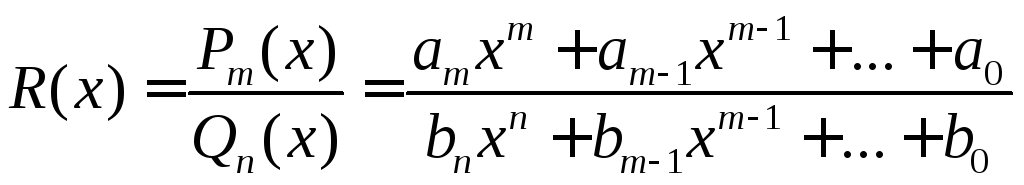
Если , то дробь называетсяправильной, если тонеправильной.

Рациональные дроби следующих типов называются простейшими дробями.

;

;

;

, .

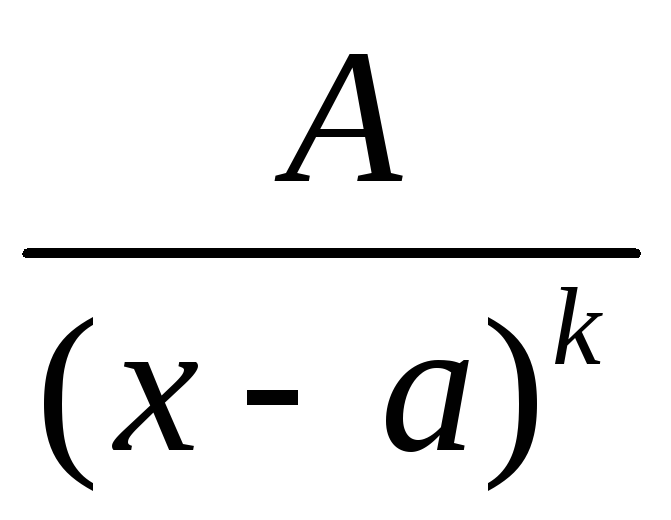
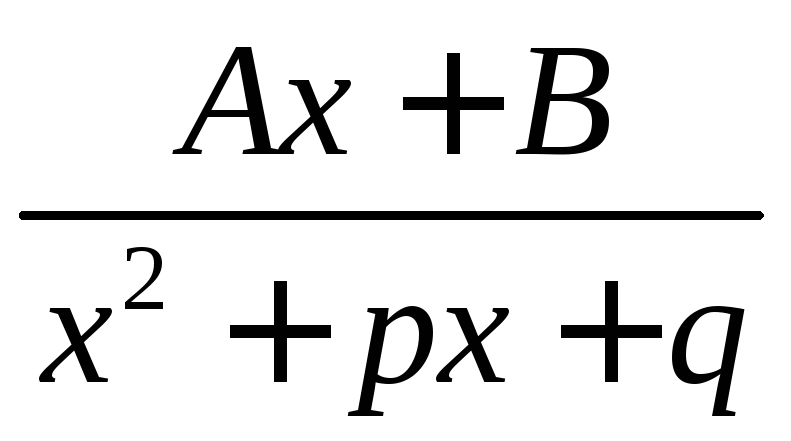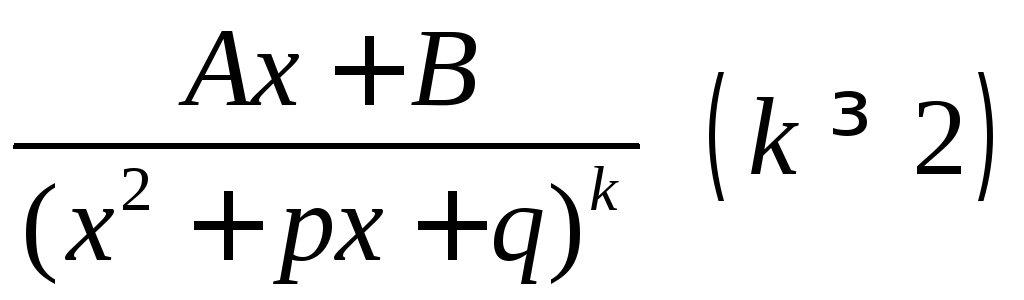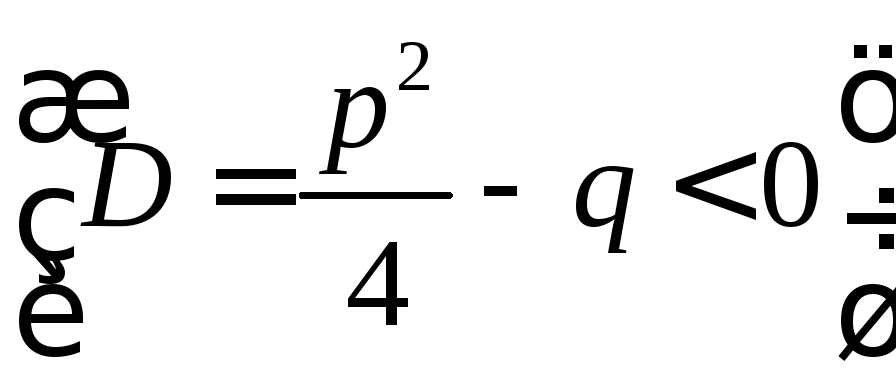2. Интегрирование простейших рациональных дробей

Дроби типов (5.1) и (5.2) интегрируются просто:

;

.

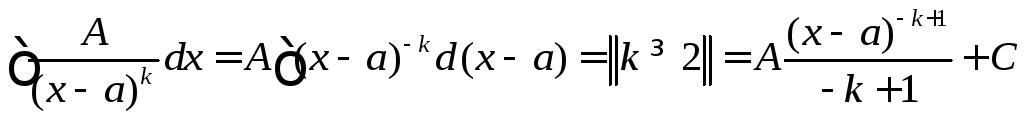Метод интегрирования простейших дробей типа был изложен в п. 4. Интегрирование дробей типа довольно громоздко и здесь излагаться не будет.

3. Интегрирование правильных рациональных дробей

Метод интегрирования состоит в разложении правильной дроби в сумму простейших дробей и почленном интегрировании этой суммы:

а) сначала находится разложение знаменателя на линейные множители и квадратичные множители с отрицательным дискриминантом

б) по этому разложению находится вид разложения правильной дроби в сумму простейших

;

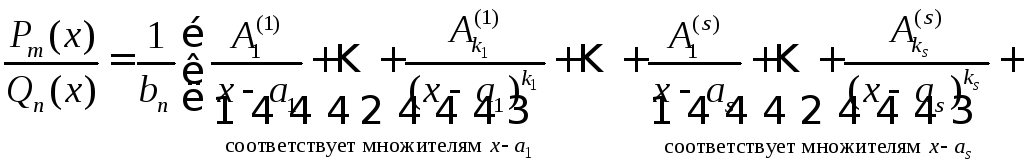
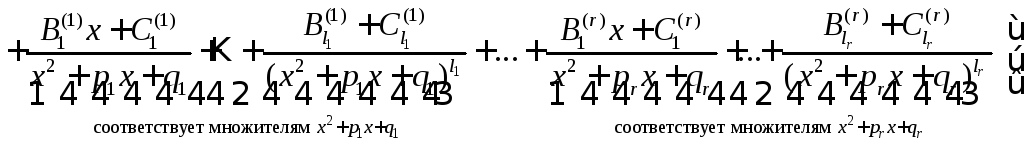с) коэффициенты в этом разложении находятся из уравнений, получающихся при приравнивании коэффициентов при одинаковых степеняхx у многочлена и многочлена, который получается в числителе правой части равенства после её к общему знаменателю (см. задачи 5.2.2 и 5.2.3).

Другой приём нахождения коэффициентов состоит в том, что после приравнивания числителей левой и правой частей равенства полагают переменнуюx равной различным числам, в первую очередь, корням знаменателя (см. задачу 5.2.1).
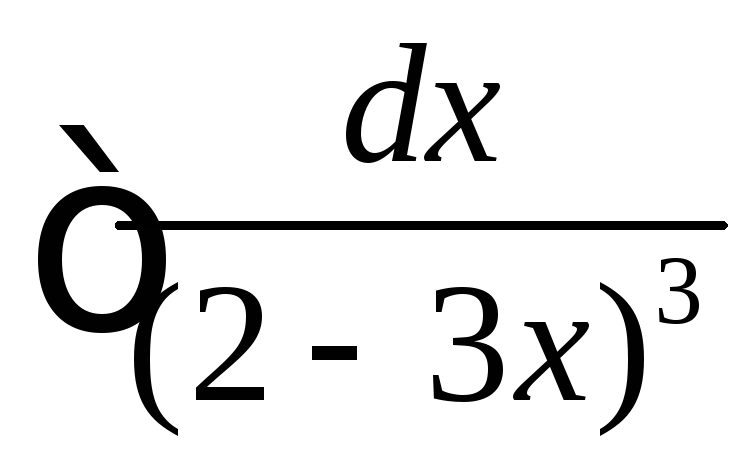
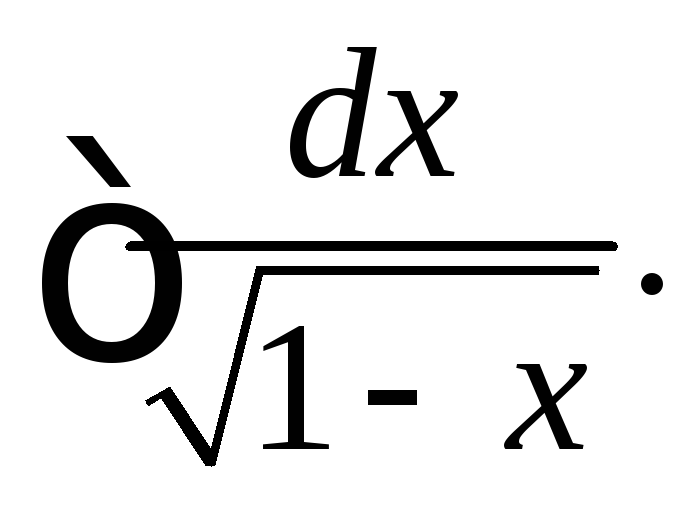
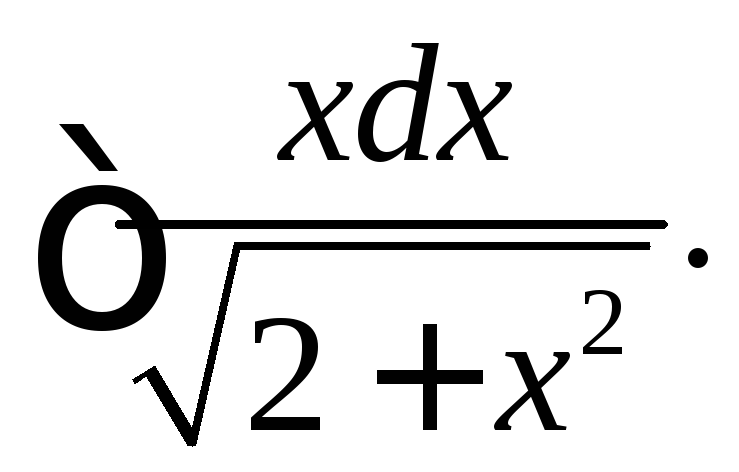
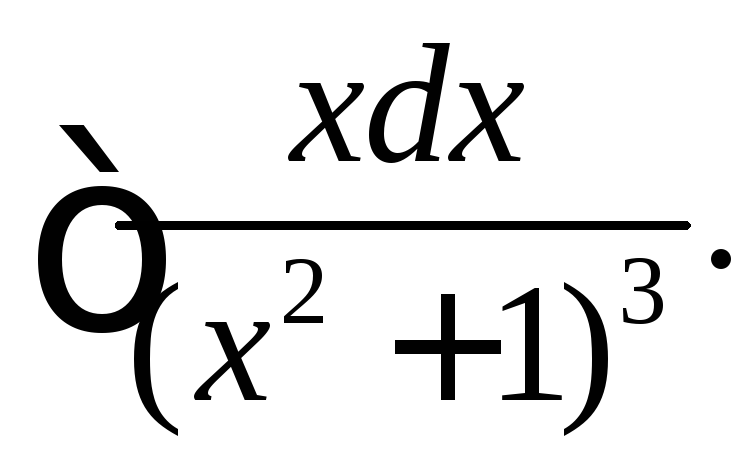
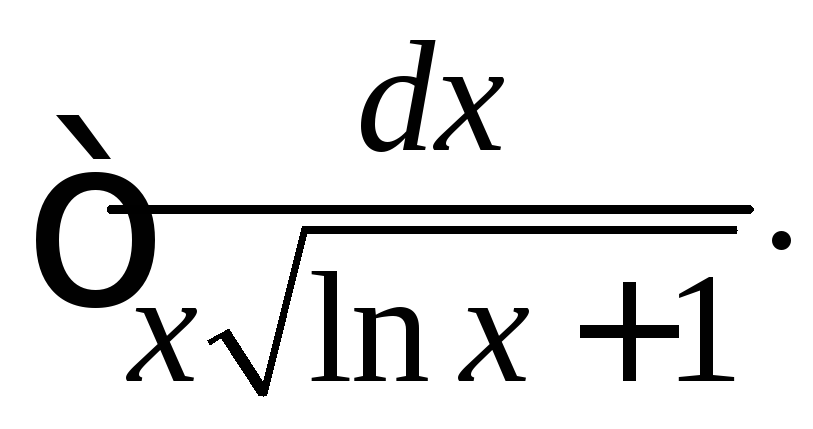
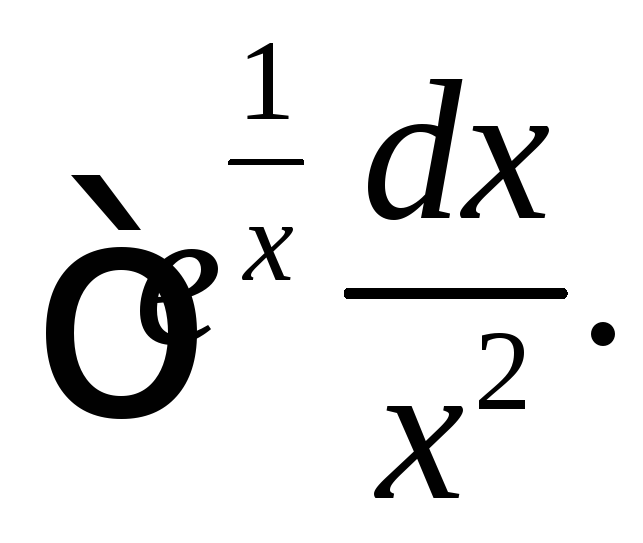
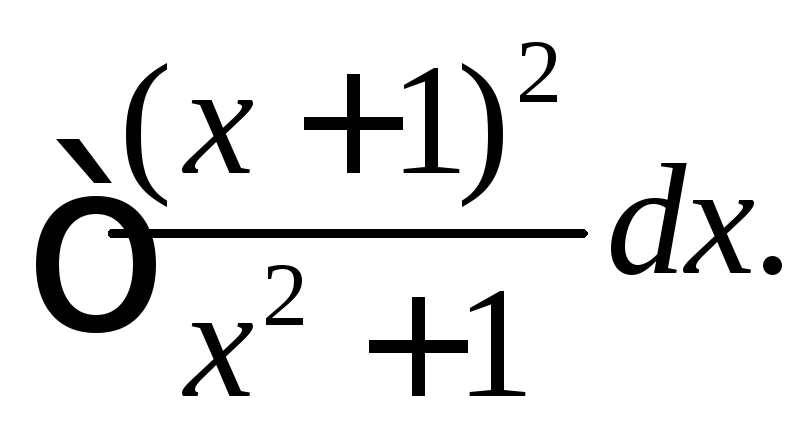
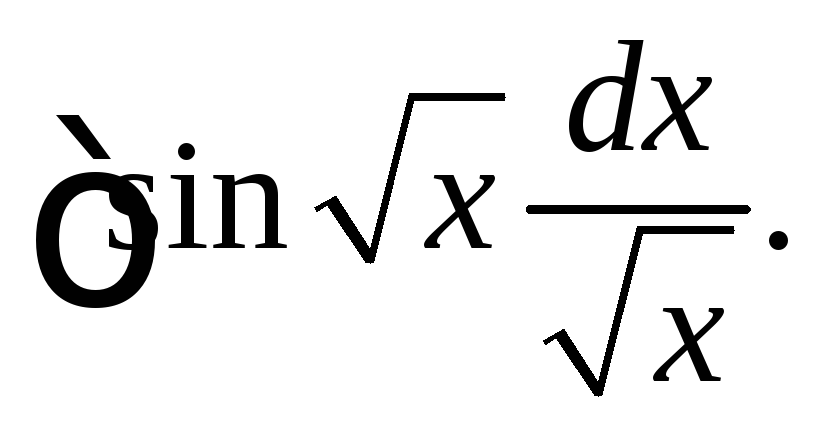
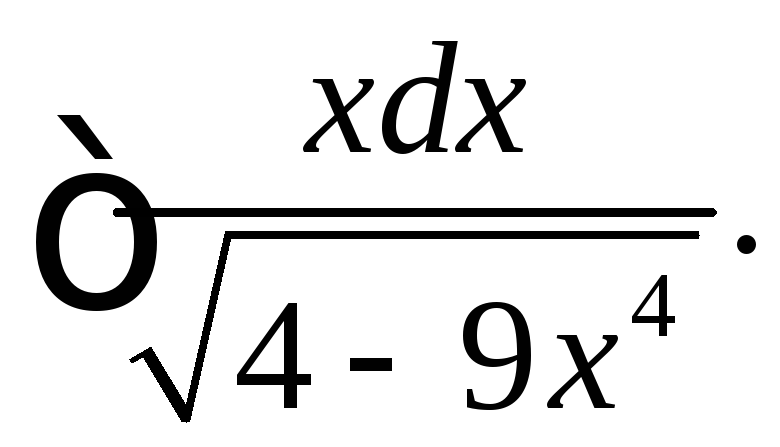
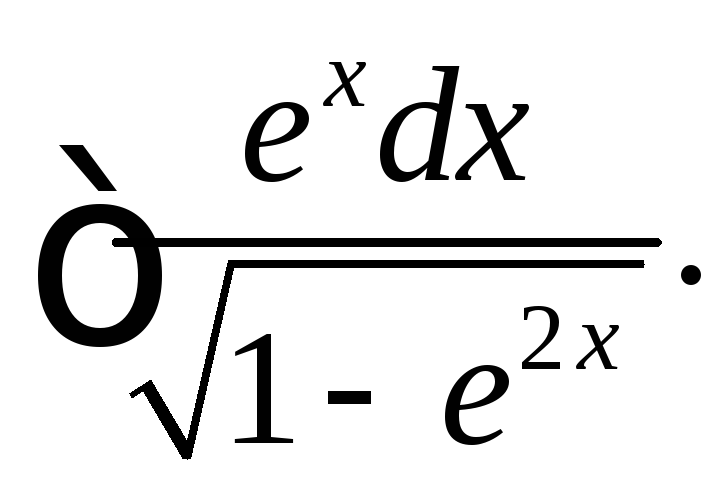
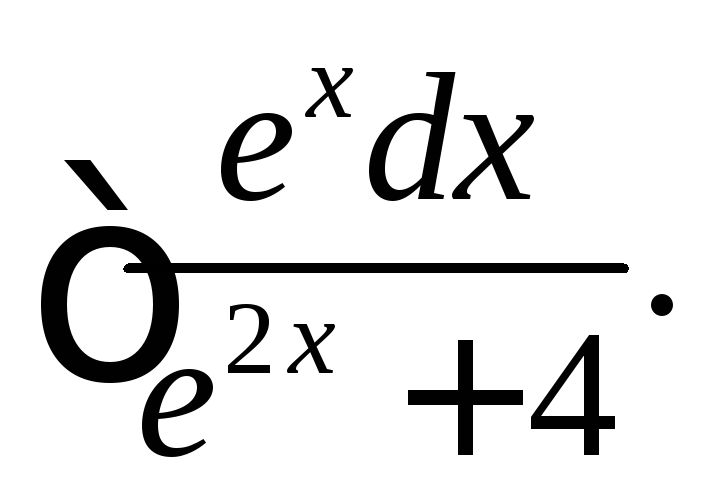
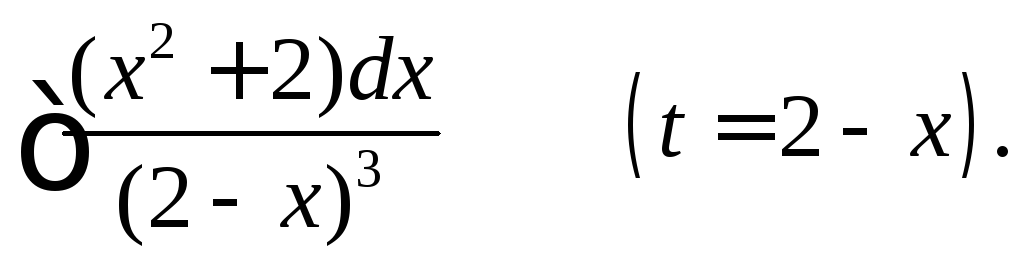
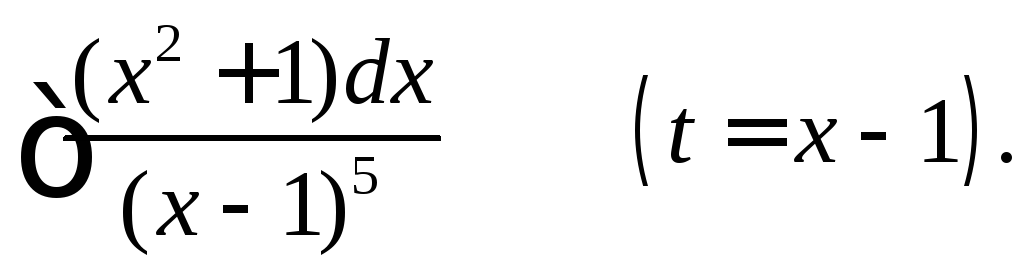
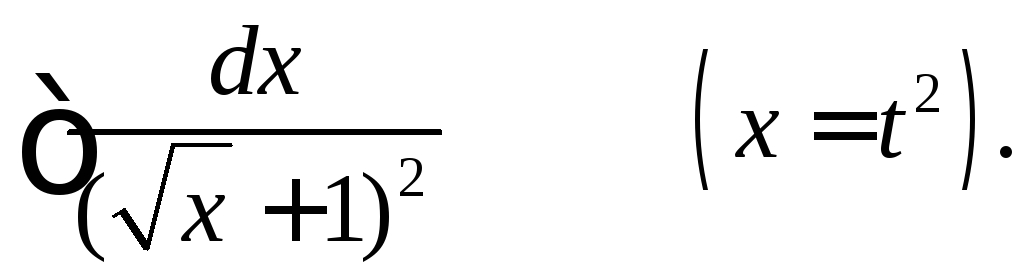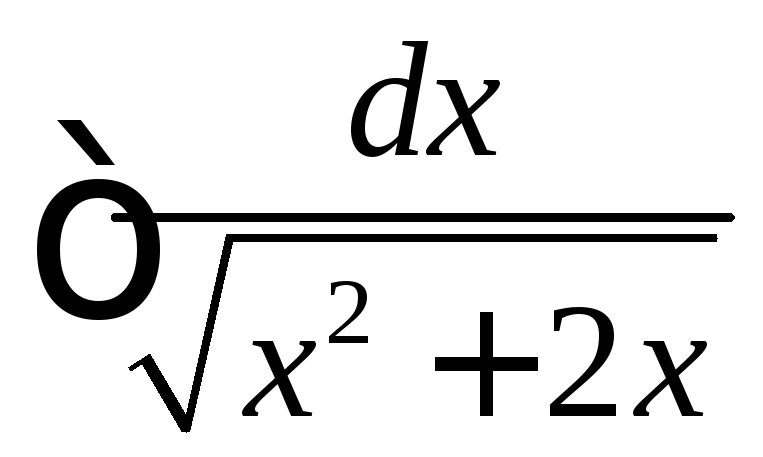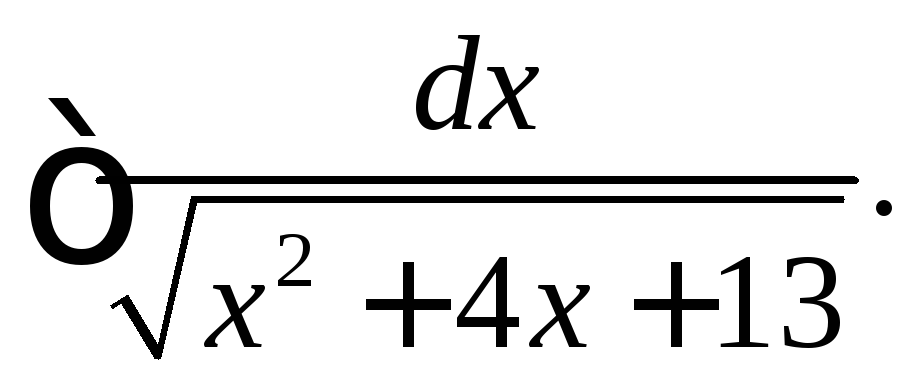
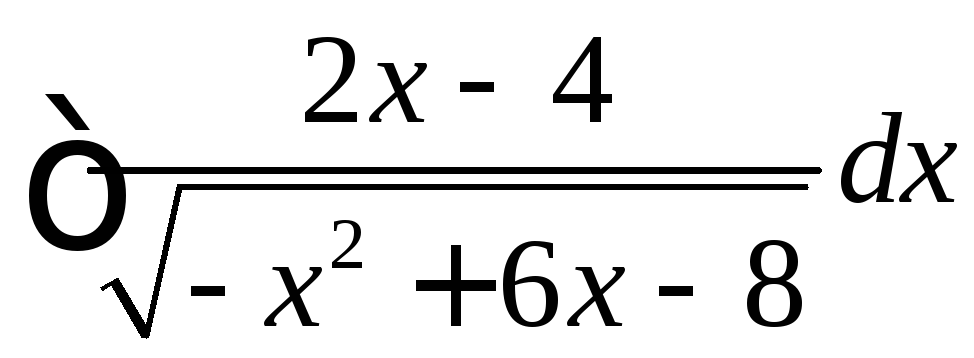