
- •Неопределенный интеграл
- •План 2009
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Интегрирование по частям
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Простейшие интегралы,
- •Интегрирование неправильных рациональных дробей
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Тригонометрические интегралы
- •Сведения из теории
- •Интегралы вида
- •Интегралы вида ,
- •Задачи для самостоятельного решения
- •Интегрирование некоторых иррациональных функций
- •Формула Ньютона-Лейбница. Интегрирование по частям в определенном интеграле. Замена переменной в определенном интеграле
- •Свойства определенного интеграла
- •Примеры решения задач
- •Несобственные интегралы с бесконечными пределами
- •Сведения из теории
- •Несобственные интегралы от неограниченных функций
- •Площадь плоской фигуры. Объем тела вращения
- •Полярные координаты. Вычисление площадей в полярных координатах
- •Длина дуги кривой. Площадь поверхности вращения
- •Библиографический список
Несобственные интегралы от неограниченных функций
Сведения из теории
Пусть
функция
![]() определена и непрерывна во всех точках
отрезка
определена и непрерывна во всех точках
отрезка![]() за исключением точки
за исключением точки![]() ,
в любой окрестности которой она
неограниченна. Тогда
,
в любой окрестности которой она
неограниченна. Тогда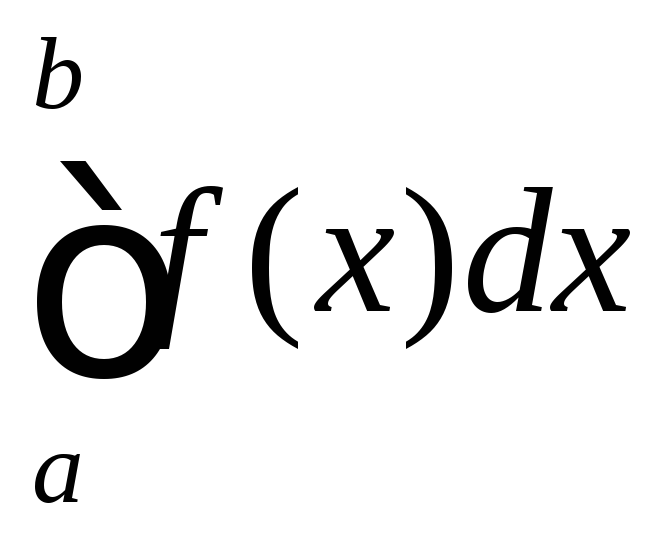 не существует в обычном смысле, как
предел интегральных сумм. В этом случае
полагают
не существует в обычном смысле, как
предел интегральных сумм. В этом случае
полагают
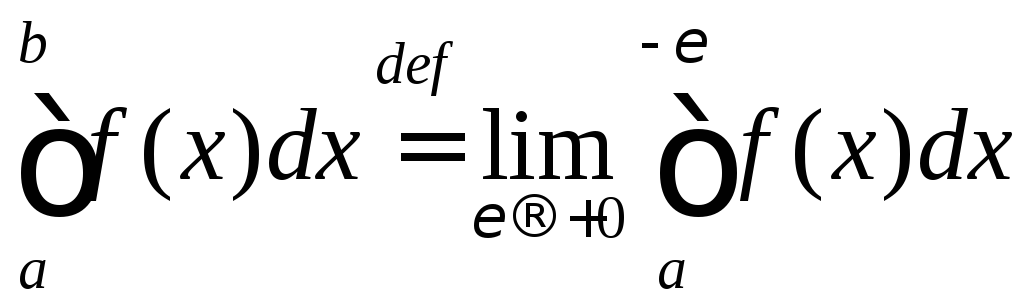 при
при
![]() ,
,
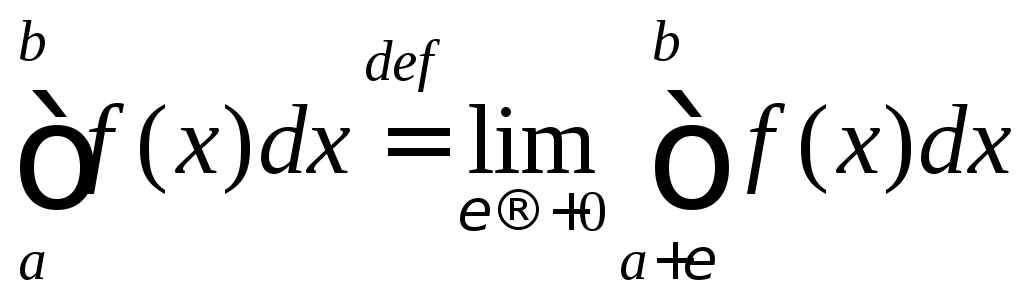 при
при
![]() ,
,
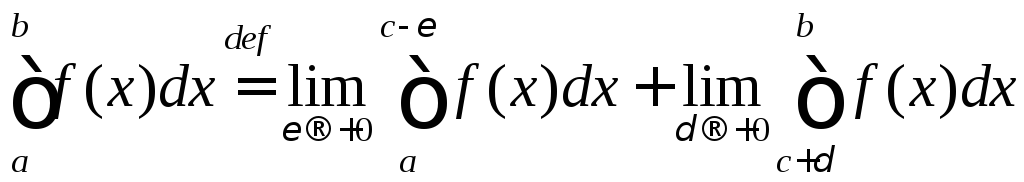 при
при
![]() .
.
Если пределы, стоящие в правых частях этих формул, существуют и конечны, то соответствующие интегралы называют сходящимися, в противном случае – расходящимися.
Примеры решения задач
Вычислить несобственный интеграл
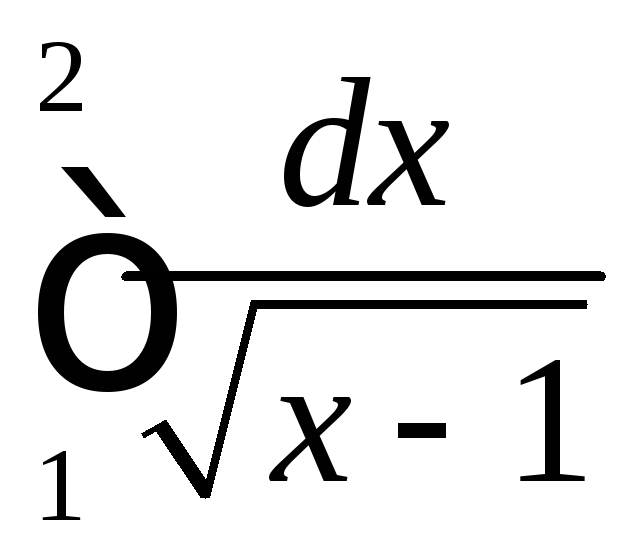 (или доказать его расходимость).
(или доказать его расходимость).
◄ Подынтегральная
функция неограниченна в любой окрестности
точки
![]()
левого конца отрезка интегрирования
(
левого конца отрезка интегрирования
(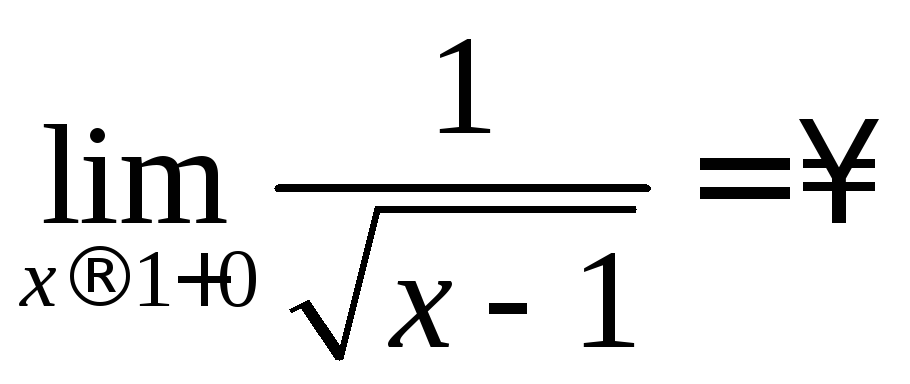 ).
Поэтому интеграл следует понимать как
несобственный:
).
Поэтому интеграл следует понимать как
несобственный:
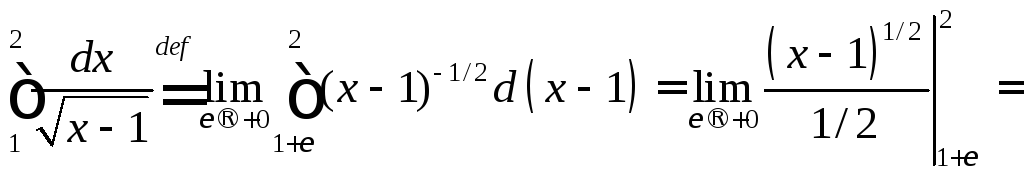
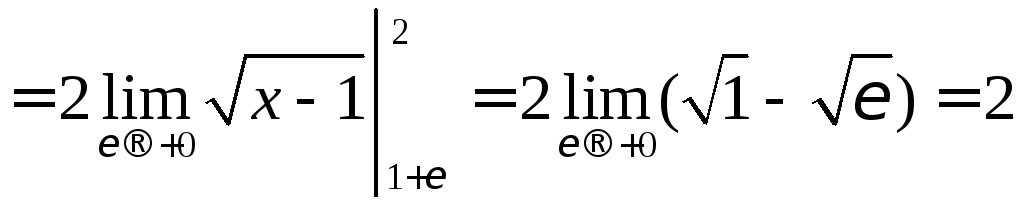 .
►
.
►
Вычислить несобственный интеграл
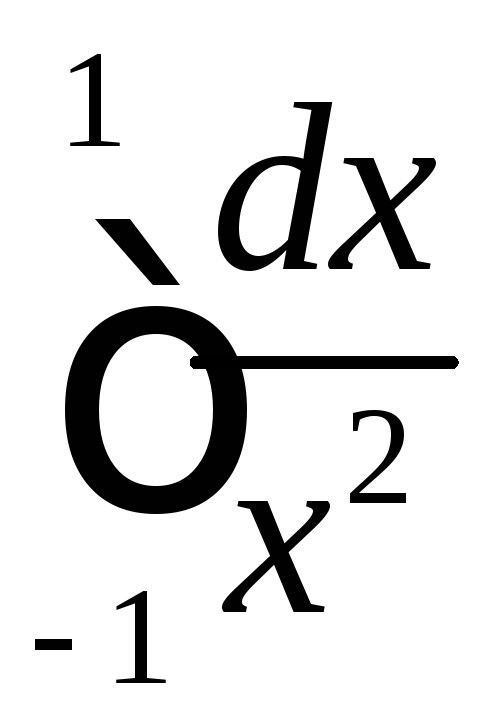 (или доказать его расходимость).
(или доказать его расходимость).
◄ Подынтегральная
функция неограниченна в любой окрестности
точки
![]() ,
лежащей внутри отрезка интегрирования
,
лежащей внутри отрезка интегрирования![]() (
(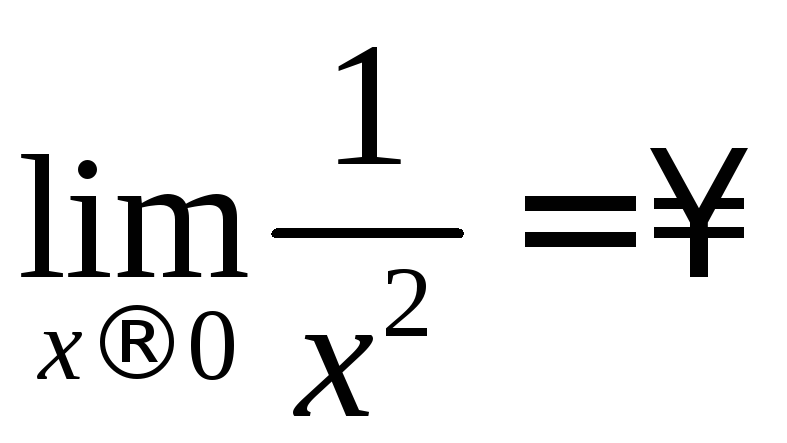 ).
Поэтому, интеграл является несобственным.
).
Поэтому, интеграл является несобственным.
По
определению
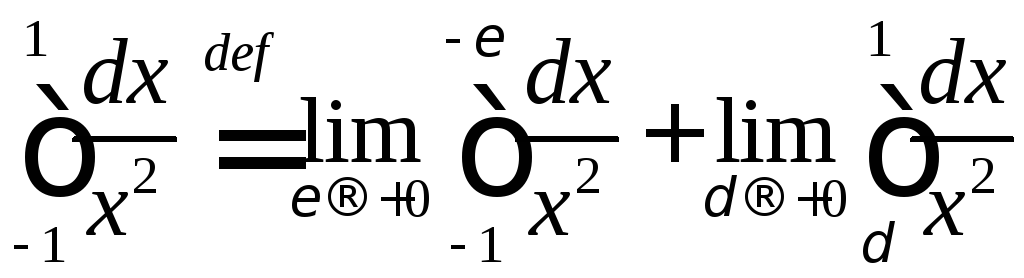 ,
если конечные пределы в правой части
этого равенства существуют, и
,
если конечные пределы в правой части
этого равенства существуют, и![]() расходится, если хотя бы один из этих
пределов бесконечен или не существует.
расходится, если хотя бы один из этих
пределов бесконечен или не существует.
Так
как на самом деле
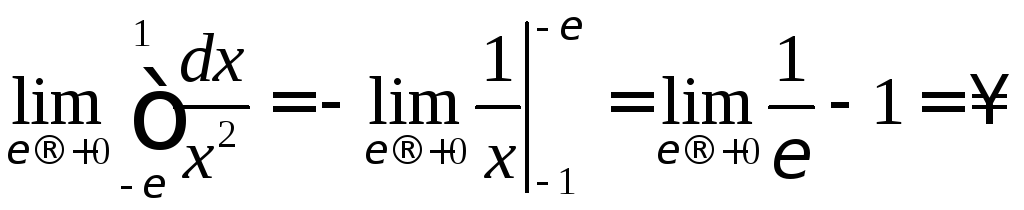 ,
,
то
![]()
расходится. ►
расходится. ►
Задачи для самостоятельного решения
В задачах 12.3.1-12.3.4 вычислить несобственные интегралы (или доказать их расходимость).
-
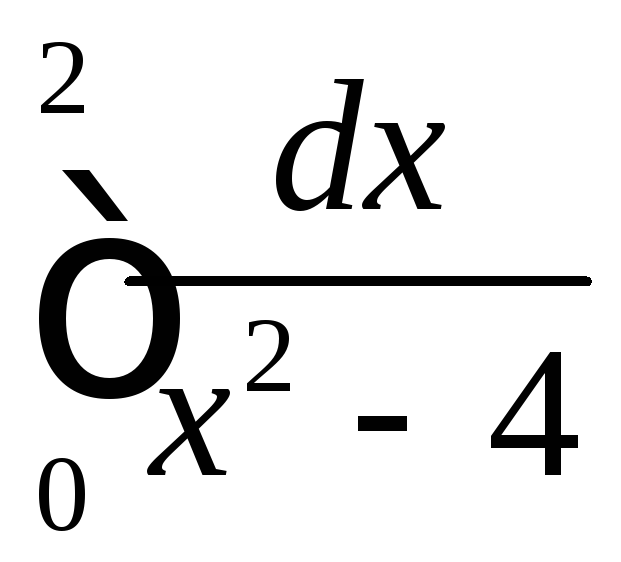 .
.
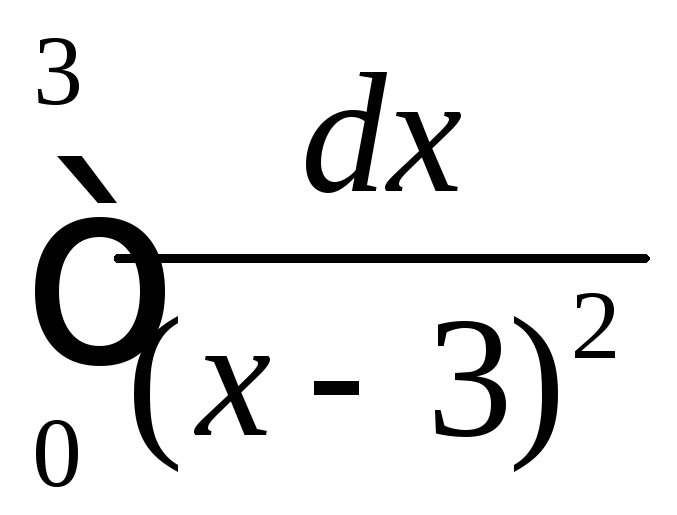 .
.
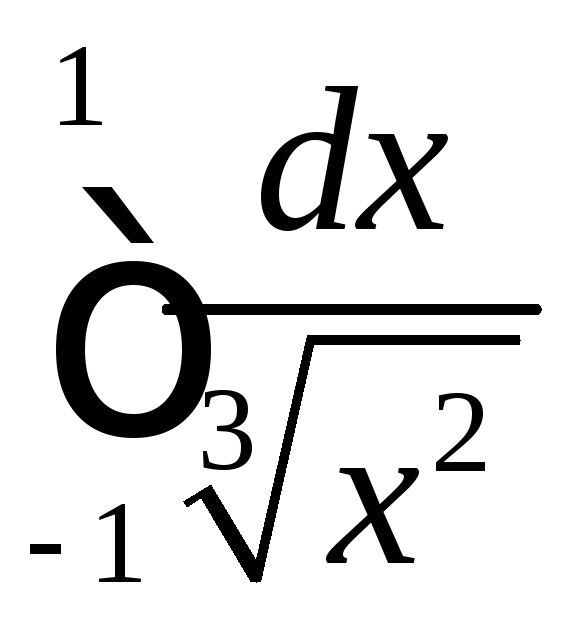 .
.
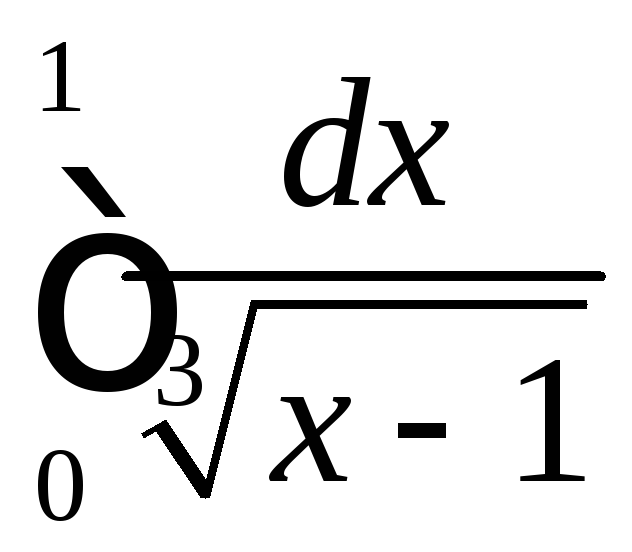 .
.
Площадь плоской фигуры. Объем тела вращения
Сведения из теории
Площадь
![]() фигуры
фигуры
![]() (рис.2),
ограниченной прямыми
(рис.2),
ограниченной прямыми
![]() и
и![]()
![]() ,
осью
,
осью![]() и графиком непрерывной функции
и графиком непрерывной функции![]() (
(![]() при
при![]() )
находится по формуле
)
находится по формуле
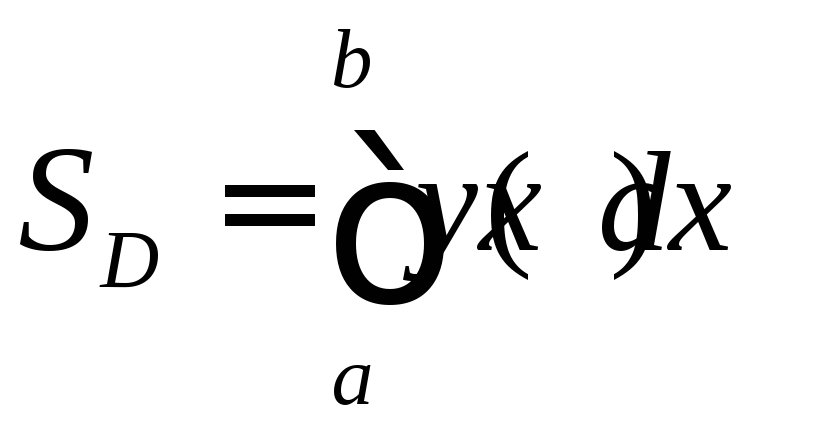 .
.
Объем
![]() тела,
полученного вращением фигуры
тела,
полученного вращением фигуры
![]() вокруг оси
вокруг оси![]() (рис.3) находится по формуле
(рис.3) находится по формуле
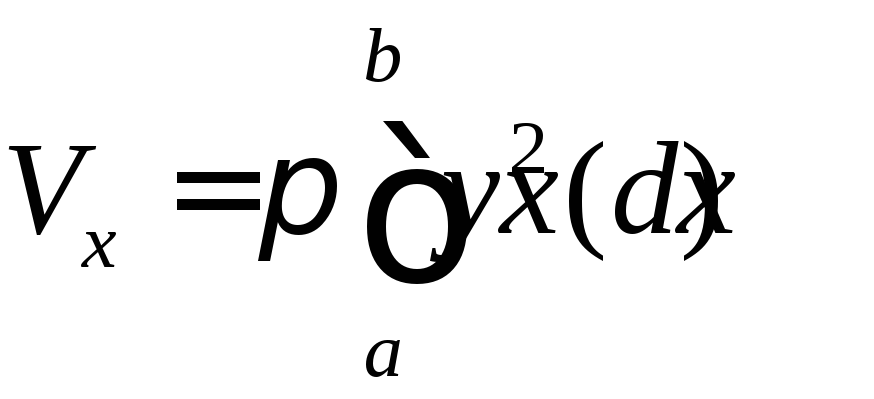 .
.
Площадь
фигуры
![]() (рис.4), ограниченной прямыми
(рис.4), ограниченной прямыми![]() и
и![]()
![]() ,
графиками непрерывных функций
,
графиками непрерывных функций![]() и
и![]() (
(![]() при
при![]() ),
находится по формуле
),
находится по формуле
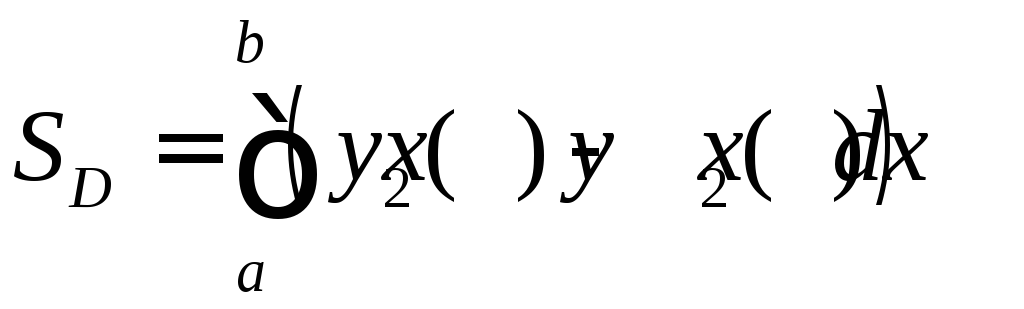 .
.
Примеры решения задач
Вычислить площадь фигуры
 ,
заданной неравенствами
,
заданной неравенствами
![]() ,
,
![]() .
.
◄ Фигура
![]() изображена на рис.5. Она ограничена
прямыми
изображена на рис.5. Она ограничена
прямыми![]() и
и![]() ,
графиком функции
,
графиком функции![]() (
(![]() при
при![]() )
и осью
)
и осью![]() .
Поэтому её площадь можно найти по формуле
.
.
Поэтому её площадь можно найти по формуле
.
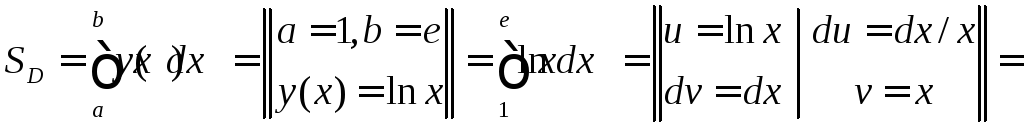
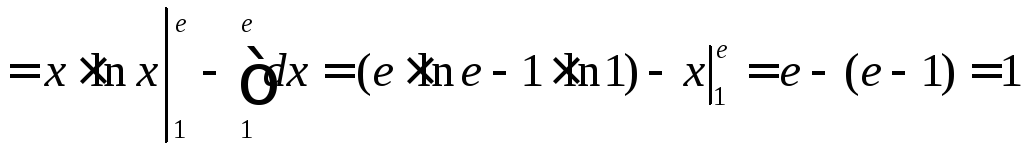 .
►
.
►
Вычислить площадь фигуры
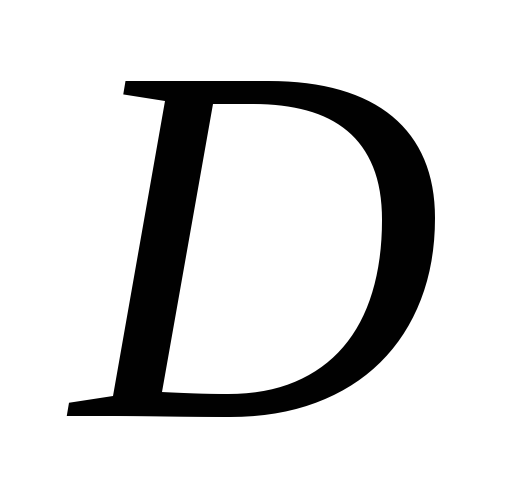 ,
ограниченной линиями
,
ограниченной линиями
![]() ,
,
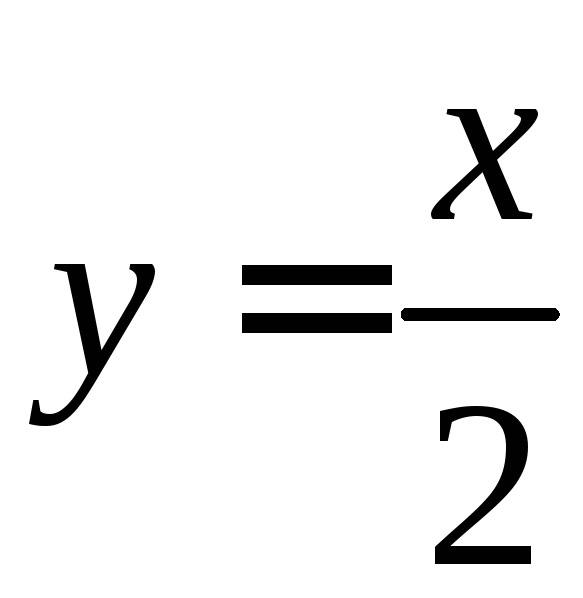 ,
,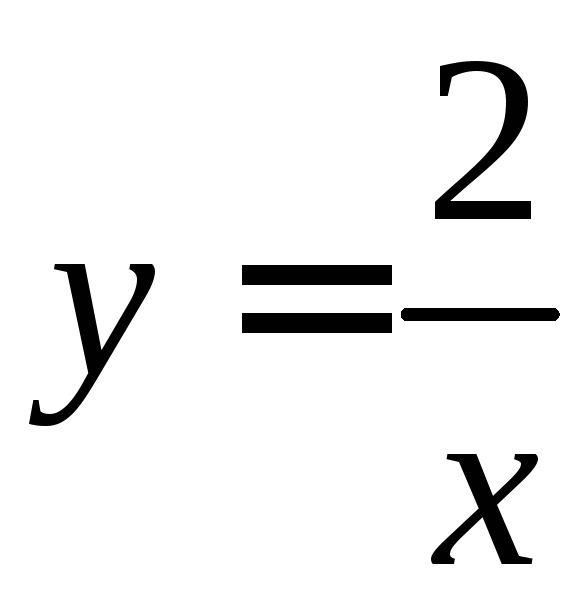 (
(![]() ).
).
◄ Форма
фигуры
![]() (рис.6)
не позволяет непосредственно применить
формулы или . Разобьем
(рис.6)
не позволяет непосредственно применить
формулы или . Разобьем
![]() на фигуры
на фигуры![]() и
и![]() ,
площади которых уже можно найти по
формуле .
,
площади которых уже можно найти по
формуле .
Найдем
сначала координаты точек
![]() и
и![]() .
.
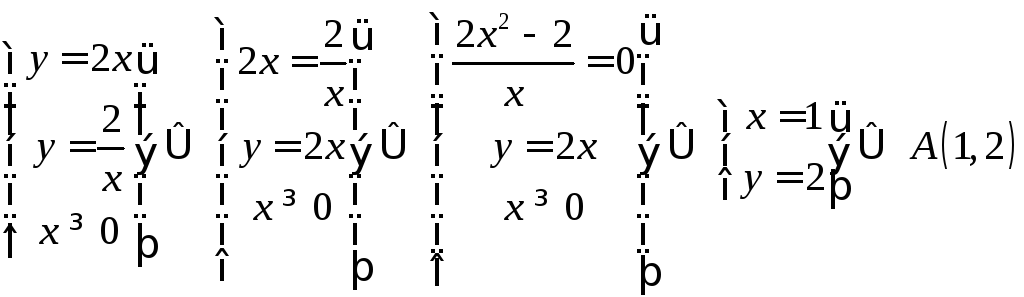 ,
,
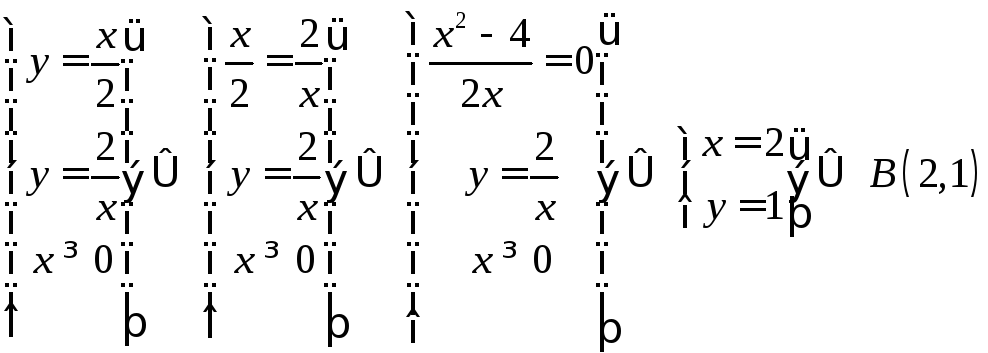 .
.
Поэтому
фигура
![]() ограничена прямыми
ограничена прямыми![]() и
и![]() ,
графиками функции
,
графиками функции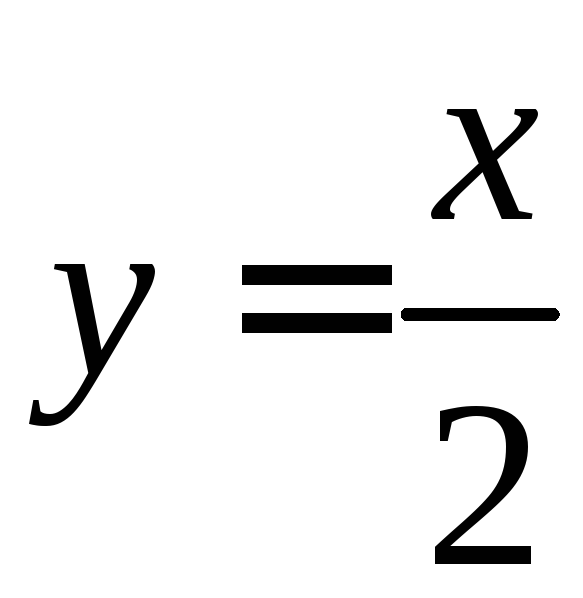 и
и![]() (при этом
(при этом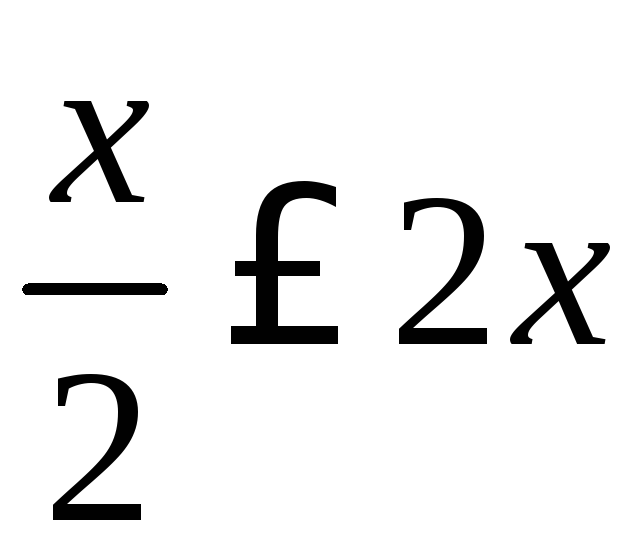 для
для![]() ).
).
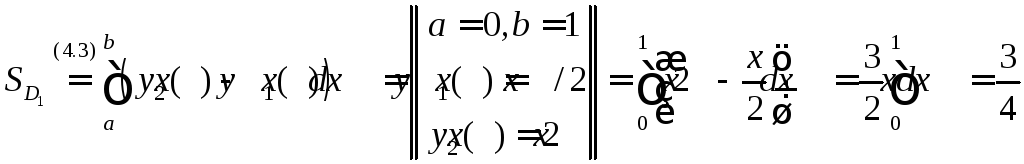 .
.
Фигура
![]() ограничена прямыми
ограничена прямыми![]() и
и![]() ,
графиками функции
,
графиками функции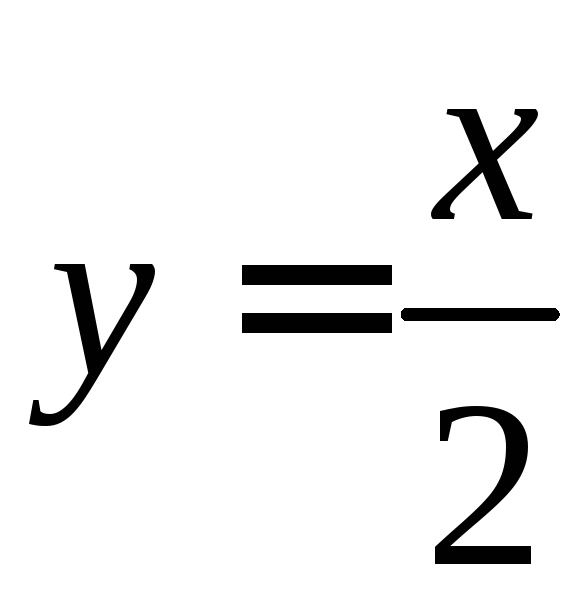 и
и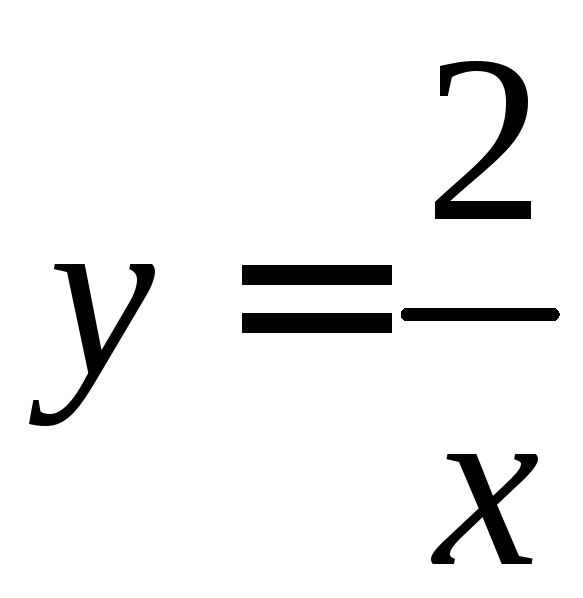 (при этом
(при этом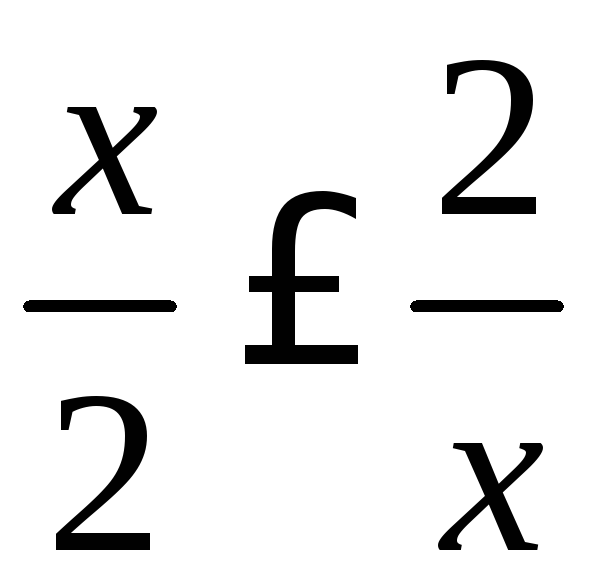 для
для![]() ).
).
Её площадь
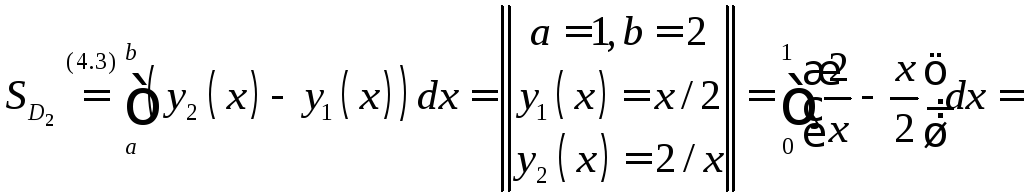
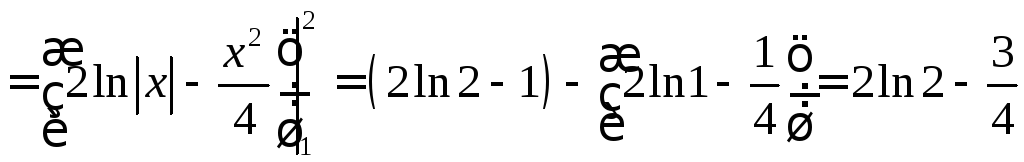 .
.
Теперь
![]() .
►
.
►
Найти площадь фигуры
 ,
ограниченной линиями
,
ограниченной линиями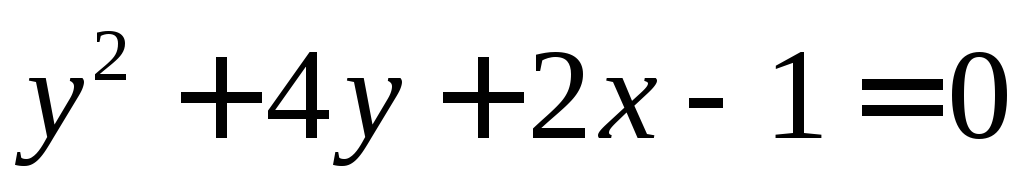 и
и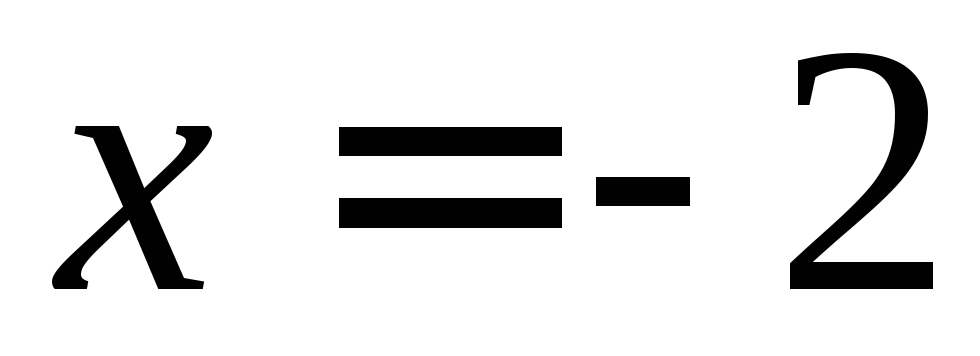 .
.
◄
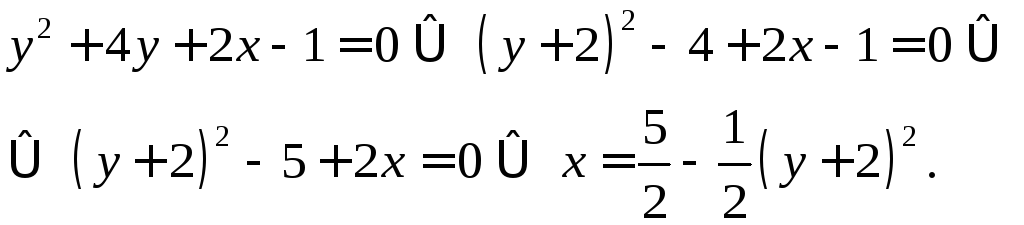
Это
уравнение параболы с вершиной в точке
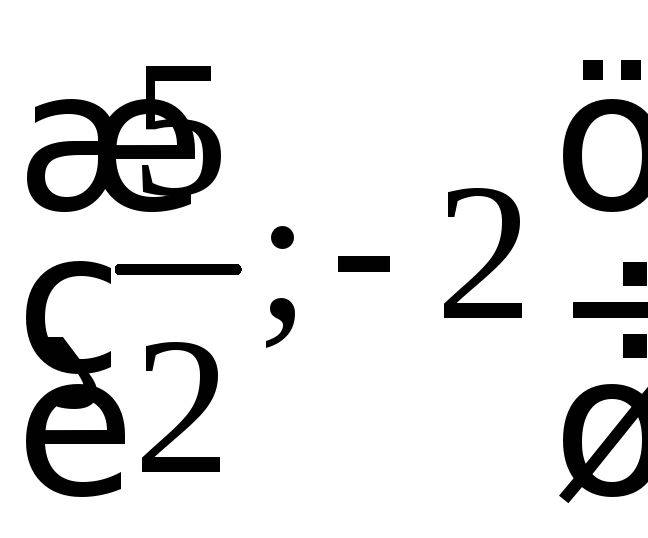 ,
осью симметрии
,
осью симметрии![]() ,
ветви параболы направлены влево(рис.7).
,
ветви параболы направлены влево(рис.7).
Найдем
координаты точек
![]() и
и![]() (рис.7).
(рис.7).
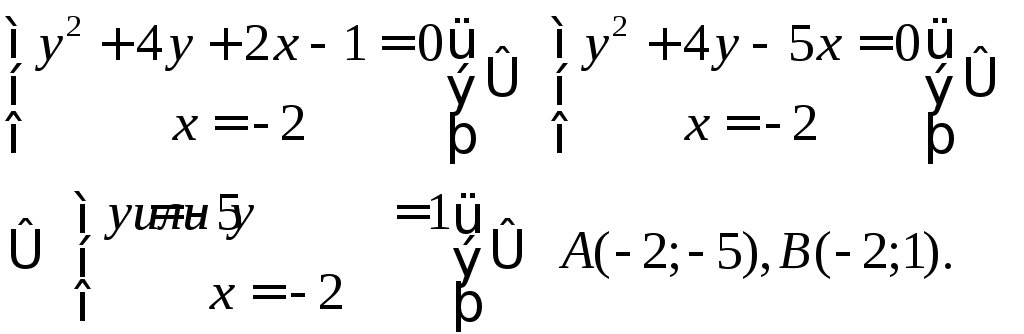
Площадь
фигуры
![]() удобнее вычислить по формуле, полученной
из формулы сменой ролей
удобнее вычислить по формуле, полученной
из формулы сменой ролей![]() и
и![]() .
Фигура
.
Фигура![]() ограничена прямыми
ограничена прямыми![]() и
и![]() ,
графиками функции
,
графиками функции![]() и
и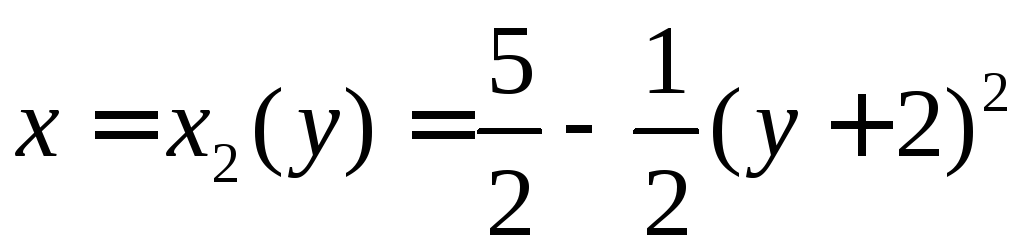 ,
поэтому
,
поэтому
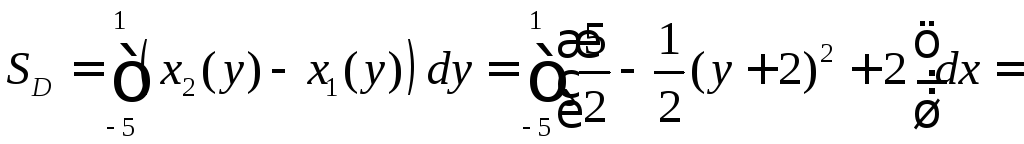
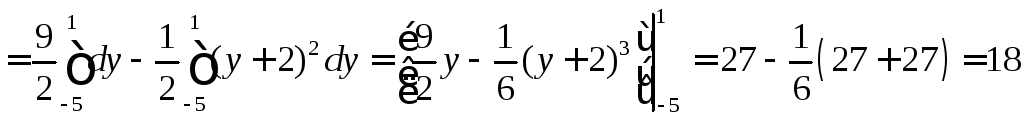 .
►
.
►
Вычислить площадь фигуры
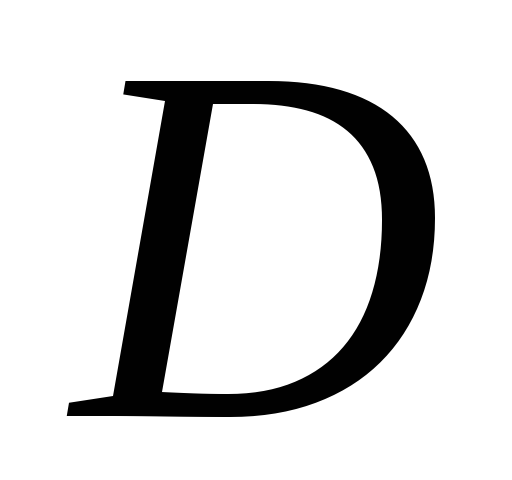 ,
ограниченной эллипсом
,
ограниченной эллипсом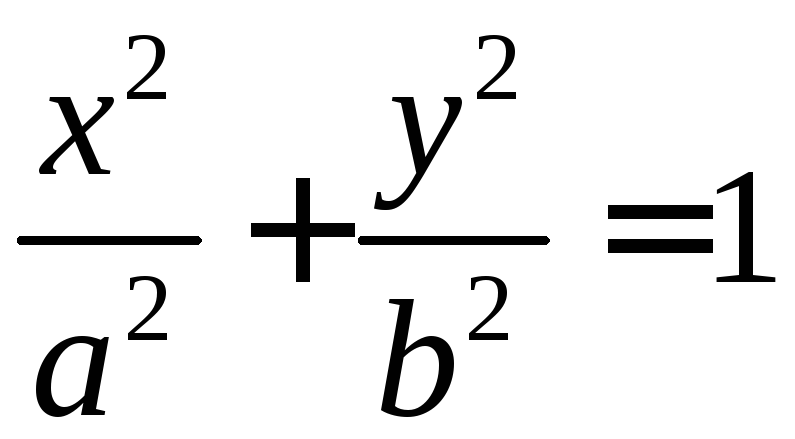 (рис.8).
(рис.8).
◄ В
силу симметрии эллипса относительно
осей координат, достаточно найти площадь
той части
![]() фигуры
фигуры![]() ,
которая расположена в первой координатной
четверти, и тогда
,
которая расположена в первой координатной
четверти, и тогда![]() .
А так как
.
А так как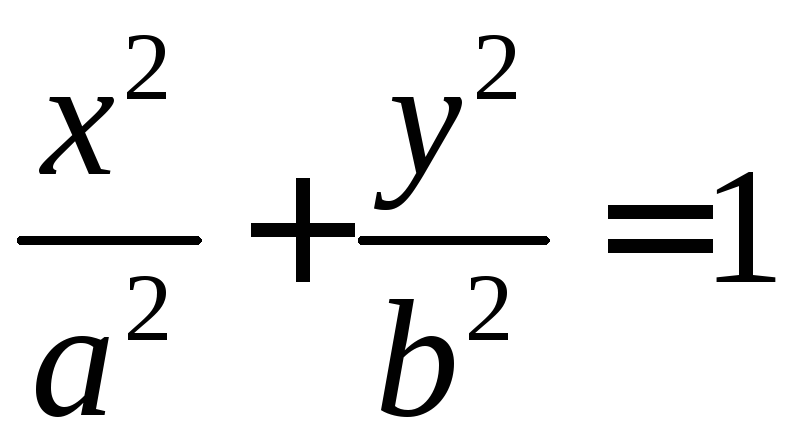 ,
,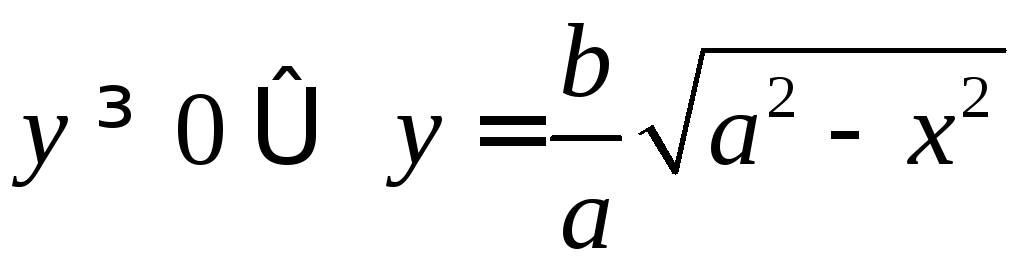 ,
то
,
то![]() ограничена прямыми
ограничена прямыми![]() и
и![]() ,
осью
,
осью![]() и графиком неотрицательной функции
и графиком неотрицательной функции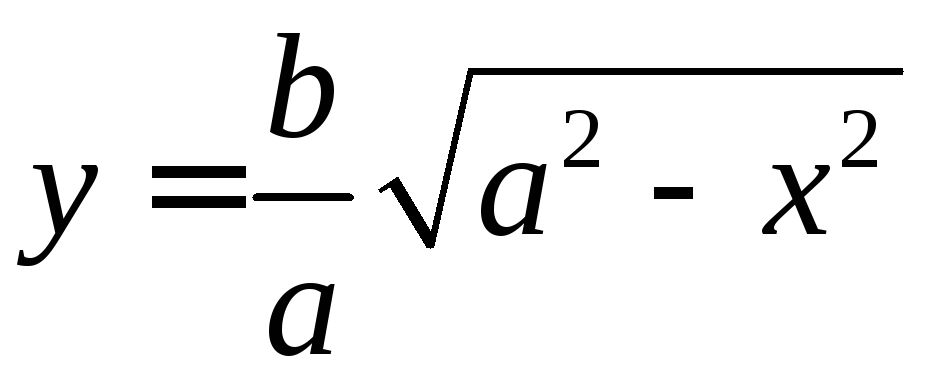 .
Её площадь
.
Её площадь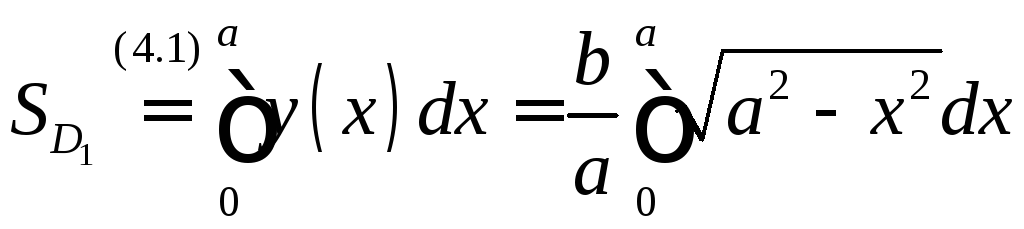 .
.
Сделаем
в интеграле замену переменного
![]() ,
, .
.
При
![]()
![]() ,
при
,
при![]()
 .
Поэтому
.
Поэтому
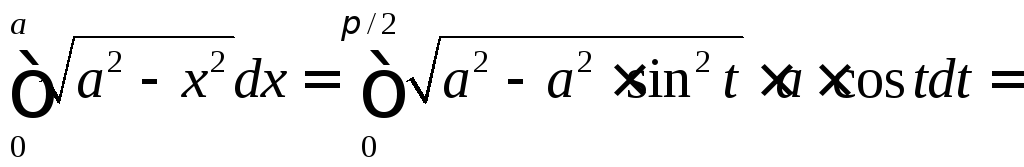
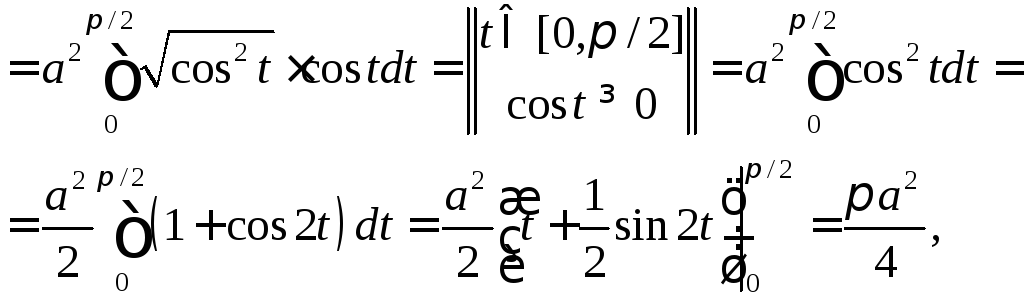
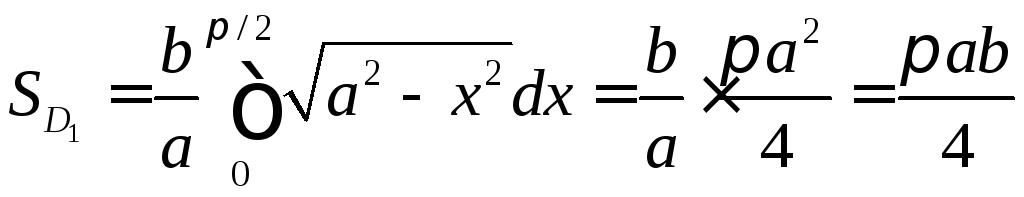 ,
,
![]() .
►
.
►
Найти объем тела, полученного вращением вокруг оси
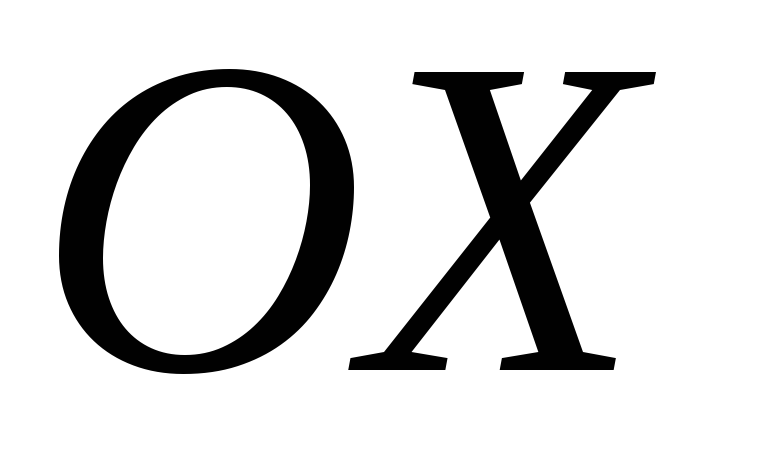 плоской фигуры, ограниченной параболой
плоской фигуры, ограниченной параболой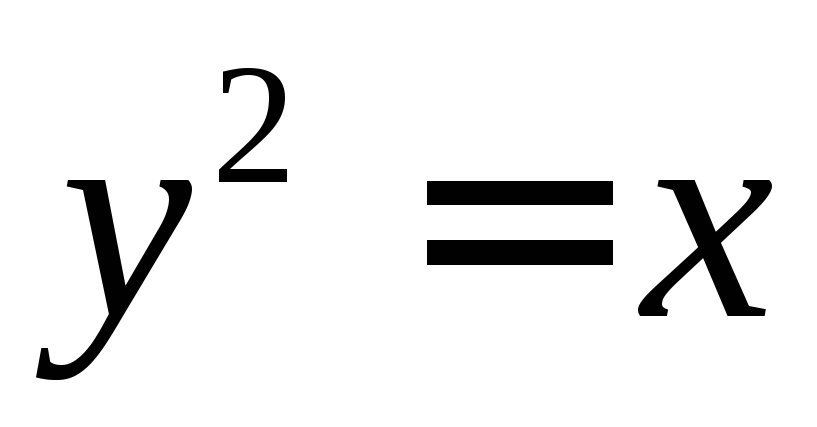 и прямой
и прямой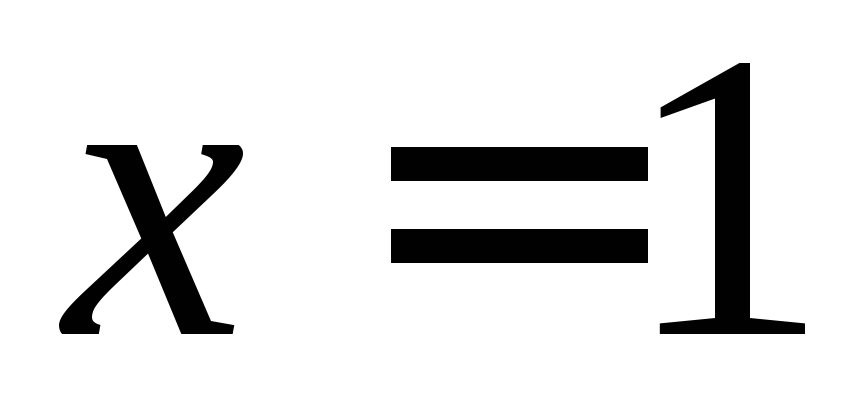 (рис.9).
(рис.9).
◄ В
силу симметрии параболы
![]() относительно оси
относительно оси![]() то же тело получается при вращении
фигуры, ограниченной прямыми
то же тело получается при вращении
фигуры, ограниченной прямыми![]() и
и![]() ,
осью
,
осью![]() и верхней половиной параболы
и верхней половиной параболы![]() .
Поэтому объем
.
Поэтому объем![]() тела можно найти по формуле
тела можно найти по формуле
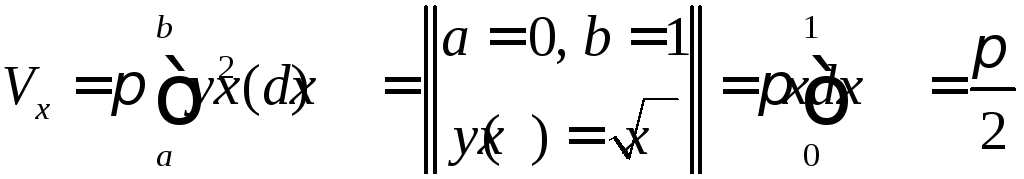 .
►
.
►
Задачи для самостоятельного решения
В задачах 13.3.1-13.3.10 найти площади фигур, заданных ограничивающими их линиями или неравенствами.
|
|
|
|
|
|
|
|
|
|
Найти объем конуса (рис.10).
В
следующих задачах найти объемы тел,
полученных вращением вокруг оси
![]() плоских фигур, ограниченных указанными
линиями.
плоских фигур, ограниченных указанными
линиями.
Эллипсом
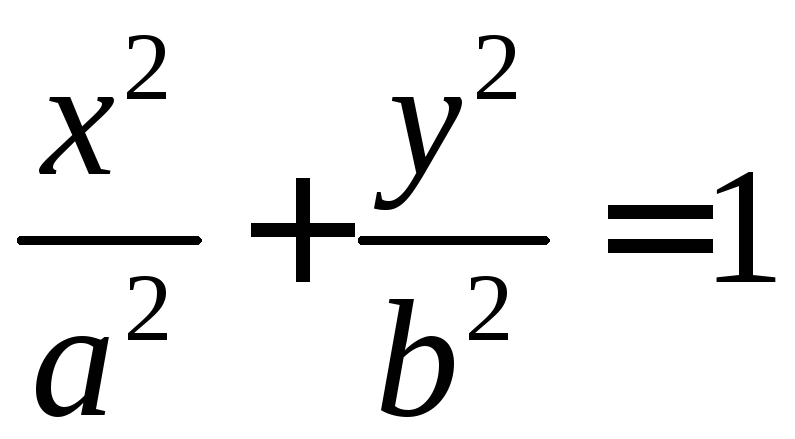 (рис.8).
(рис.8).Гиперболой
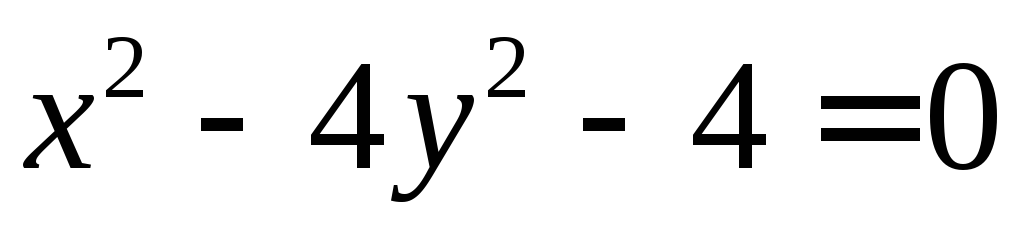 и прямой
и прямой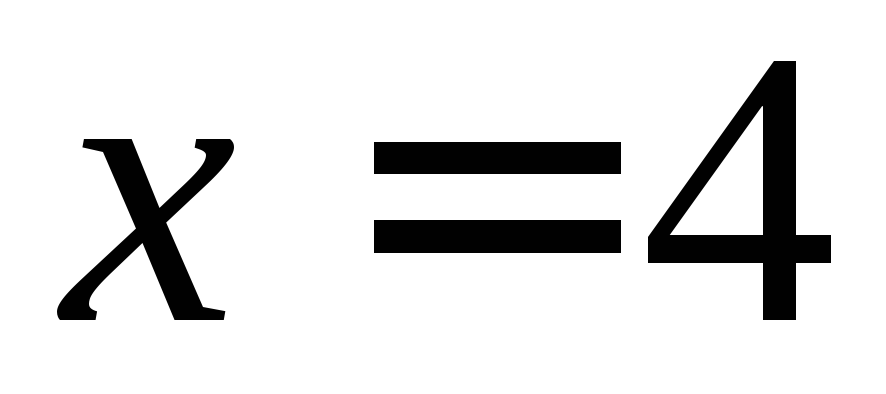 .
.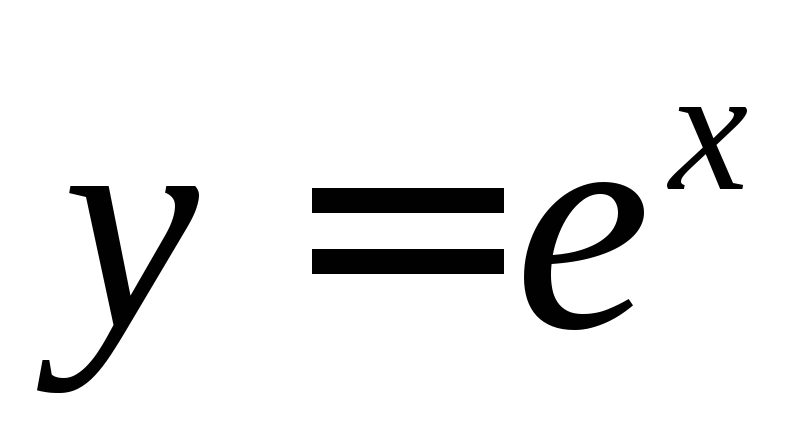 ,
,
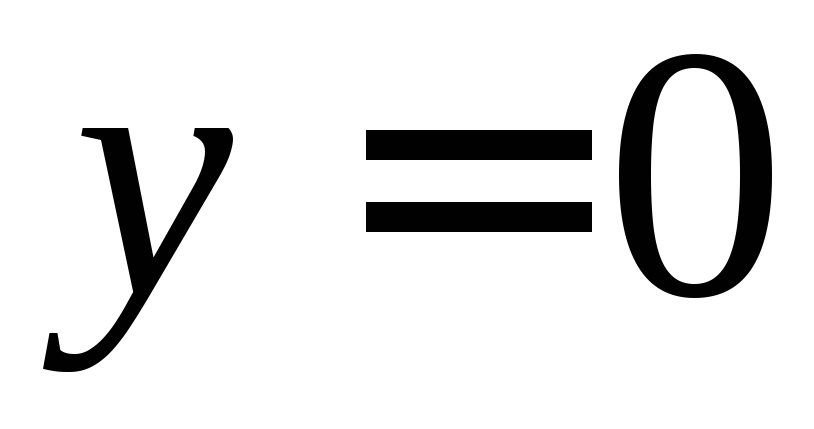 ,
,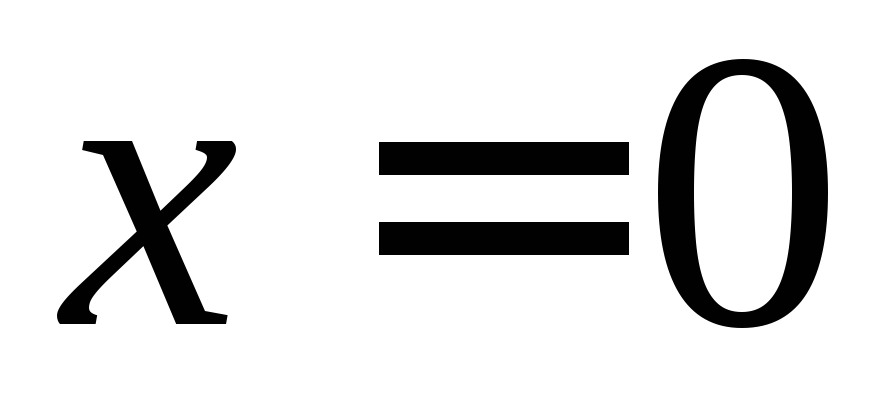 ,
,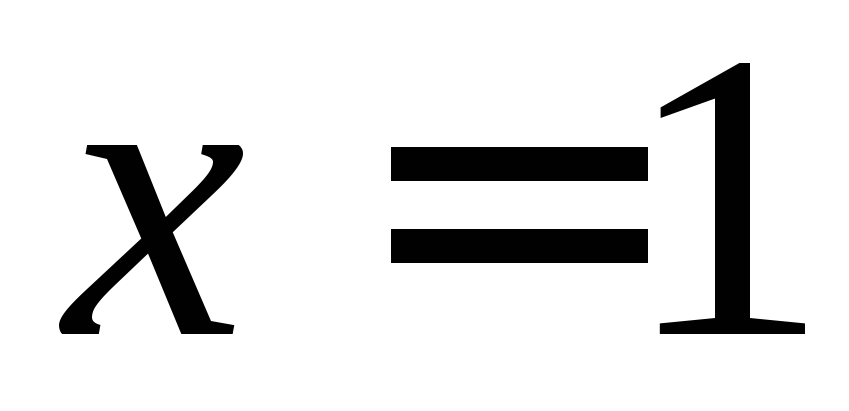 .
.

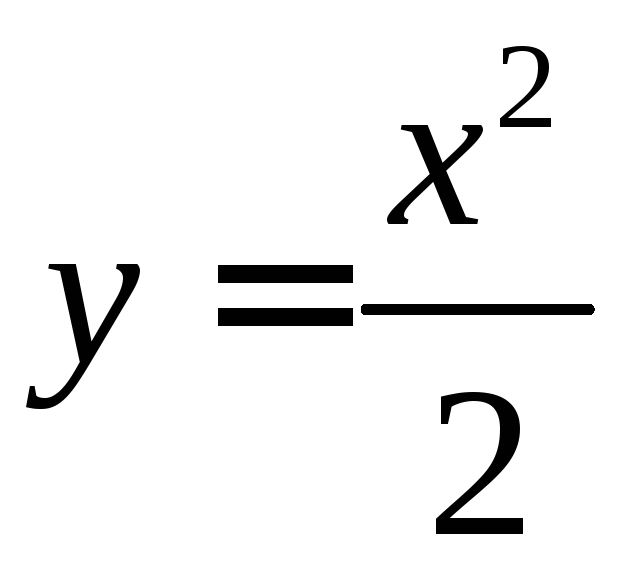 ,
,
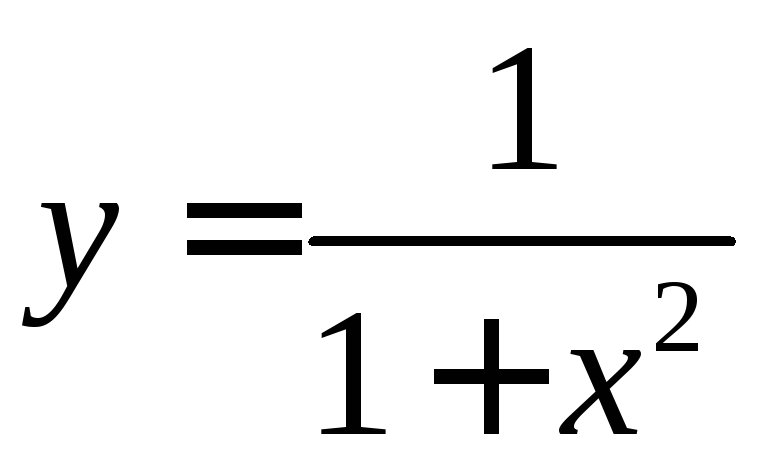
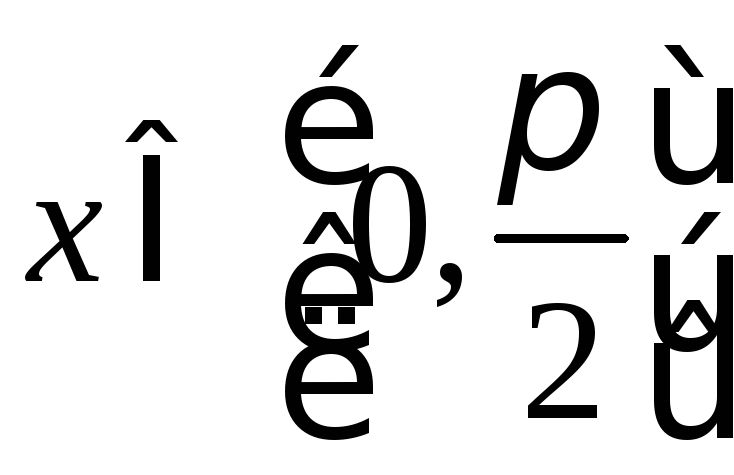 ,
,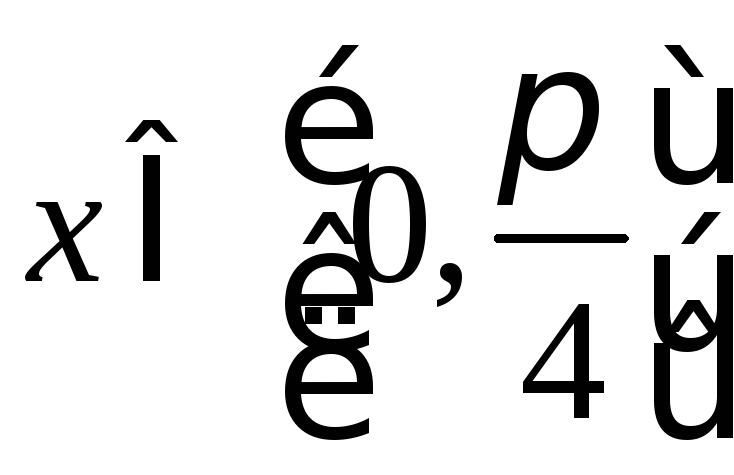 ,
, ,
,