Примеры решения задач
Убедиться, что функция
является первообразной функции
на
.
◄
Действительно,
при любом
.
►
Убедиться, пользуясь определением, что
.
◄ Так
как
,
то
.
►
Вычислить
.
◄ При вычислении этого интеграла применим свойства 2, 3 и табличный интеграл 1.
.
►
Вычислить
.
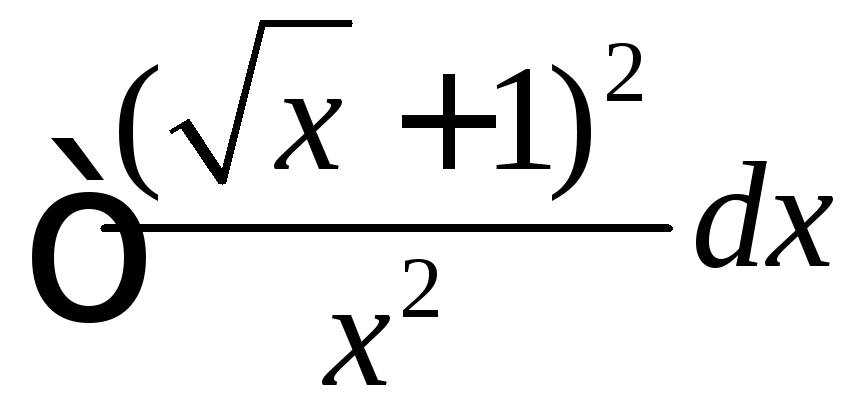◄ При вычислении этого интеграла применим тождественные преобразования (возведение суммы в квадрат и деление суммы на число), свойства 2, 3 и табличные интегралы 1 и 2.
.
►
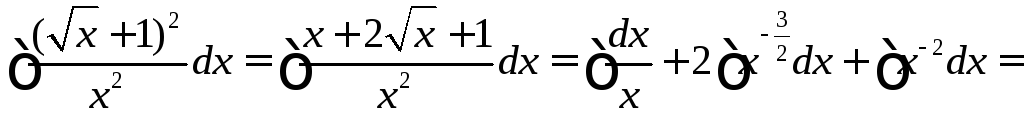
Вычислить
.
◄ При вычислении этого интеграла применим тождественные преобразования, свойство 2 и табличный интеграл 10
.►
Вычислить
.
◄ При вычислении интеграла применим тождественные преобразования, свойство 2 и табличный интеграл 11
.
►
Вычислить
.
◄ При вычислении применяем тождественные преобразования, свойство 2 и табличный интеграл 9.
.
►
Задачи для самостоятельного решения
Вычислить интегралы, используя таблицу интегралов и свойства 1-3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
.
.
.
Метод замены переменных
Сведения из теории
Существует два варианта этого метода.
Метод подведения под дифференциал
Предположим,
что подынтегральное выражение удалось
представить в виде
(это преобразование называетсяподведением
функции
под знак дифференциалаd).
Тогда
,
где
после вычисления интеграла, стоящего
в правой части этой формулы, надо заменить
переменную u
на функцию
.
Интеграл, получившийся в результате
такого преобразования, может оказаться
«проще» исходного, например, табличным.
Метод подстановки
Пусть
функция
имеет непрерывную производную и обратную
функцию
.
Тогда
,
где после вычисления интеграла, стоящего в правой части этой формулы, надо заменить переменную t на функцию t(x).
При
удачном выборе подстановки
интеграл, стоящий справа, может оказаться
«проще исходного».
Примеры решения задач
Далее
знак
будет означать ссылку на табличный
интеграл с номеромN.
Вычислить
.
◄
.
Под знаком интеграла стоит степень
функции
,
поэтому удобно подвести
под знак дифференциала:
,
.
►
Вычислить
.
◄ Подведём
под знак дифференциала
:
так как дифференциал
,
то
.
Поэтому
.
►
Вычислить
.
◄ Так
как
,
то
и
.►
Вычислить
.
◄ Так
как
,
то
.
►
Вычислить
.
◄ Подведём
под знак дифференциала
:
.
.
►
Вычислить
.
◄Так
как
,
то
.
►
Вычислить
.
◄ Поскольку
,
то
.
►
Вычислить
.
◄
.
►
Вычислить
.
◄
.
►
Вычислить
.
◄
.
►
Вычислить
.
◄
.►
Вычислить
.
◄
.
►
Замечание.
В примерах 2.2.1-2.2.12 после замены функции
на новую переменнуюu
получались табличные интегралы. Обычно
в таком случае эту замену делают мысленно,
не оформляя ее письменно.
Вычислить
.
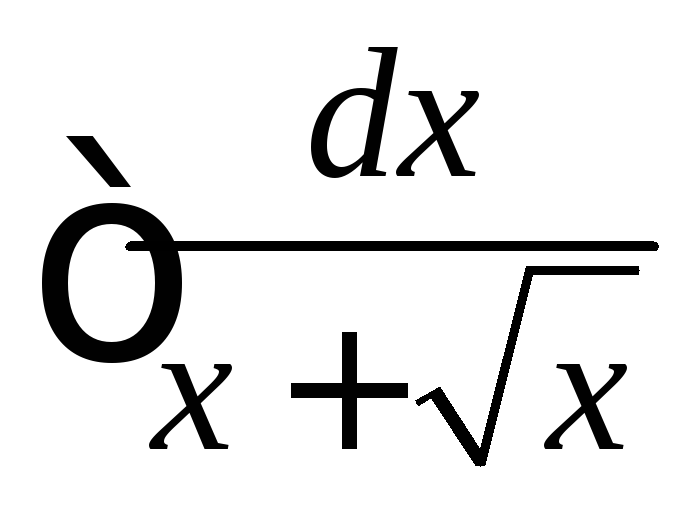◄ Сделаем
замену переменной – подстановку
.
Тогда
и
.
По формуле получим
.►
Вычислить
.
◄ Обозначим
.
Тогда
,
.
По формуле
.
►
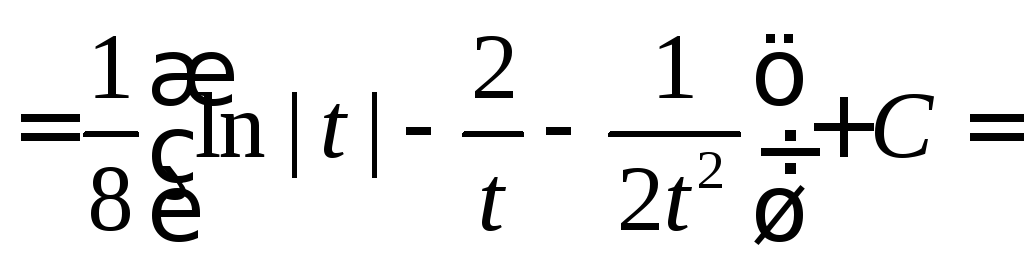
Вычислить
.
◄ Обозначим
.
Тогда
.
По формуле
.
Замечание.
Интеграл
можно вычислить и иначе. Согласно п. 4
.
►
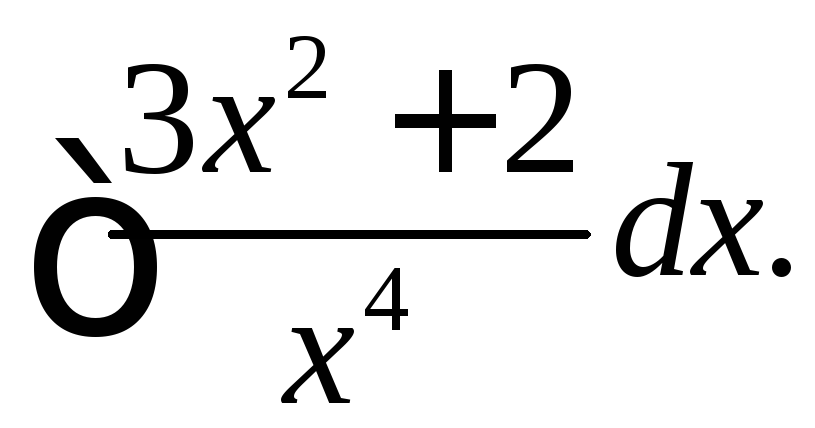