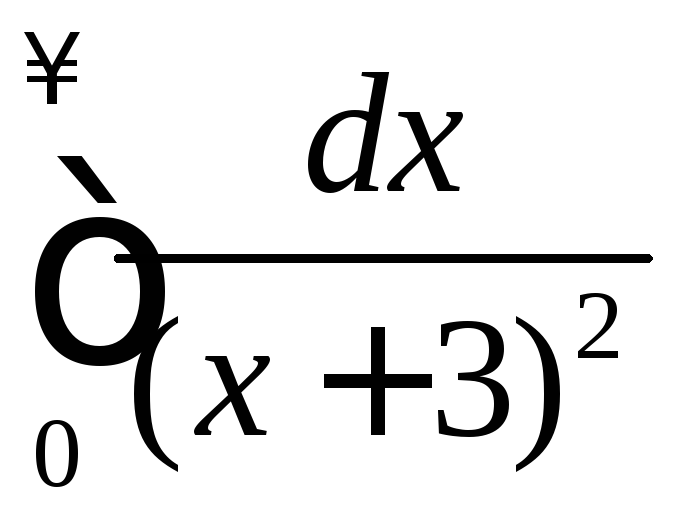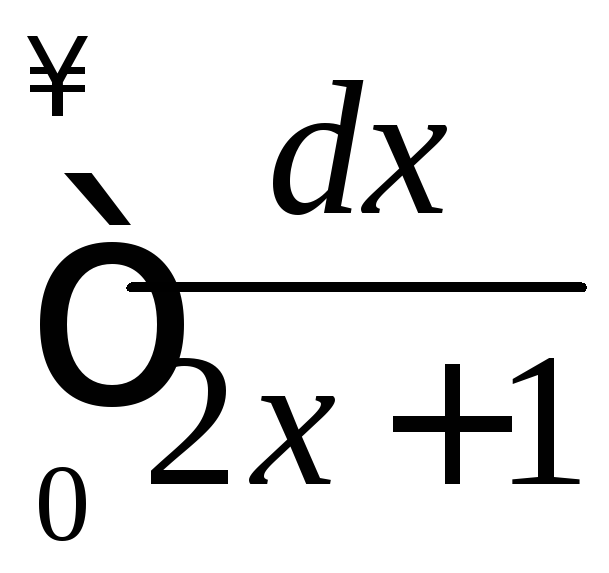- •Неопределенный интеграл
- •План 2009
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Интегрирование по частям
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Простейшие интегралы,
- •Интегрирование неправильных рациональных дробей
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Тригонометрические интегралы
- •Сведения из теории
- •Интегралы вида
- •Интегралы вида ,
- •Задачи для самостоятельного решения
- •Интегрирование некоторых иррациональных функций
- •Формула Ньютона-Лейбница. Интегрирование по частям в определенном интеграле. Замена переменной в определенном интеграле
- •Свойства определенного интеграла
- •Примеры решения задач
- •Несобственные интегралы с бесконечными пределами
- •Сведения из теории
- •Несобственные интегралы от неограниченных функций
- •Площадь плоской фигуры. Объем тела вращения
- •Полярные координаты. Вычисление площадей в полярных координатах
- •Длина дуги кривой. Площадь поверхности вращения
- •Библиографический список
Примеры решения задач
Вычислить
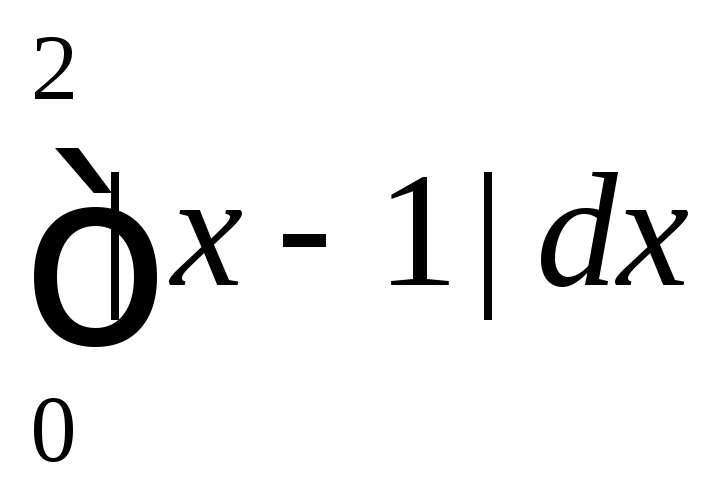 .
.
◄ Так
как
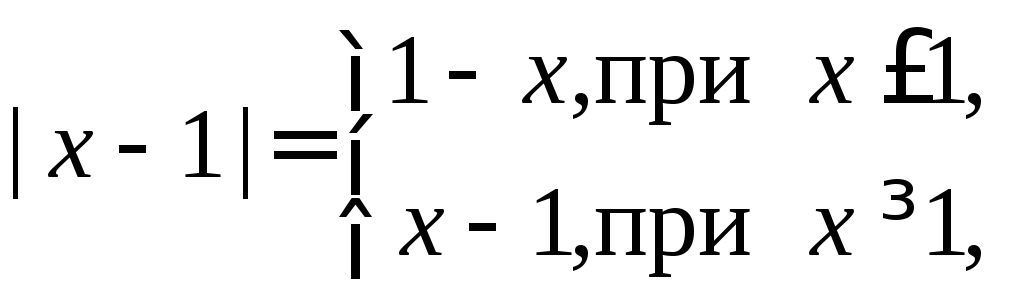
то, используя свойство аддитивности определенного интеграла, получаем
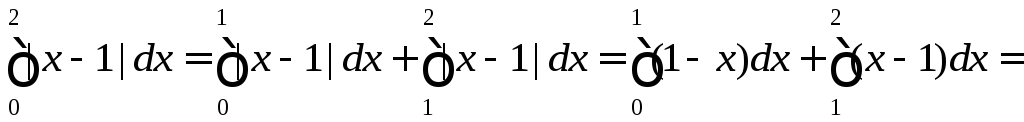
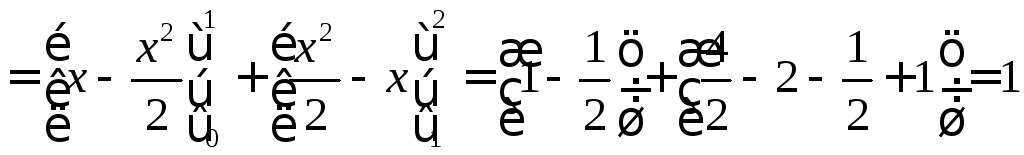 .►
.►
Доказать, что для любого
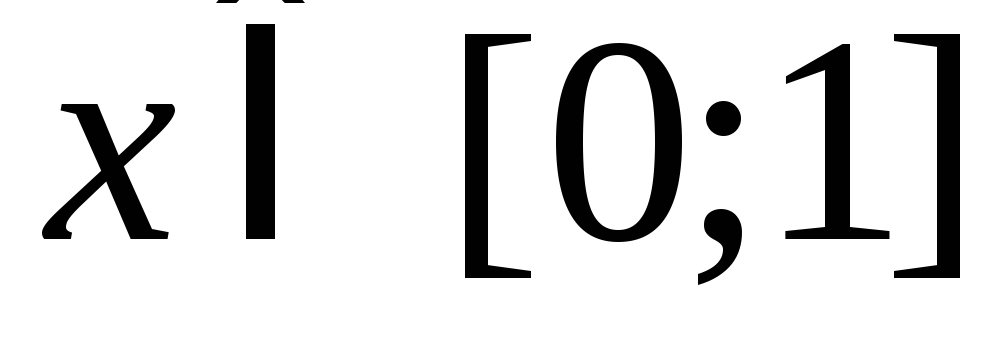
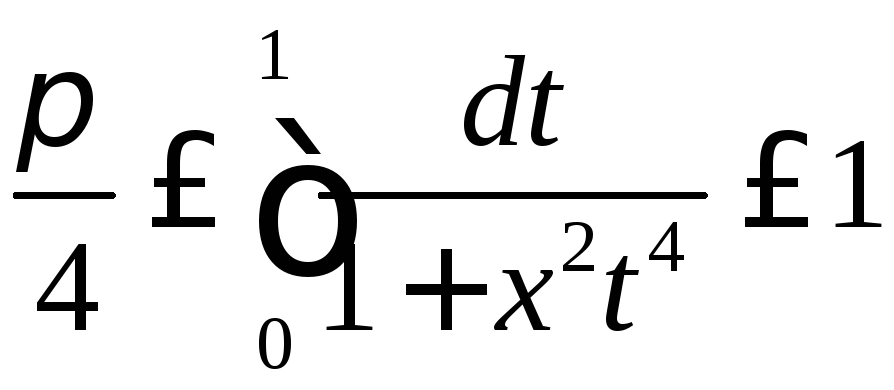 .
.
◄ Так
как
![]() ,
,![]() ,
то
,
то![]() и
и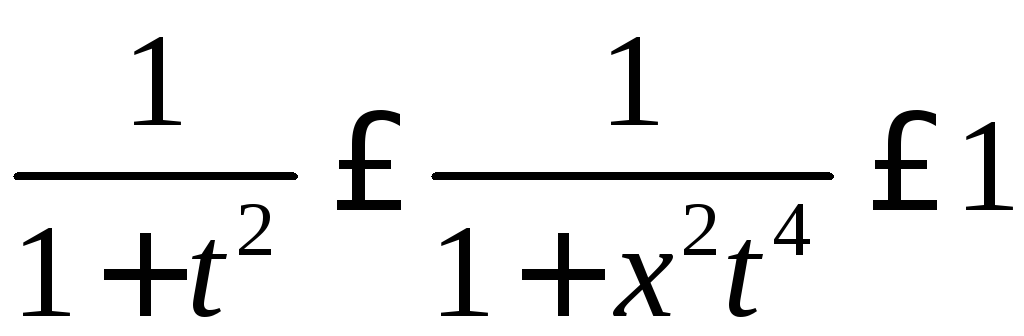 .
Согласно свойству 3 мы можем проинтегрировать
это неравенство:
.
Согласно свойству 3 мы можем проинтегрировать
это неравенство:
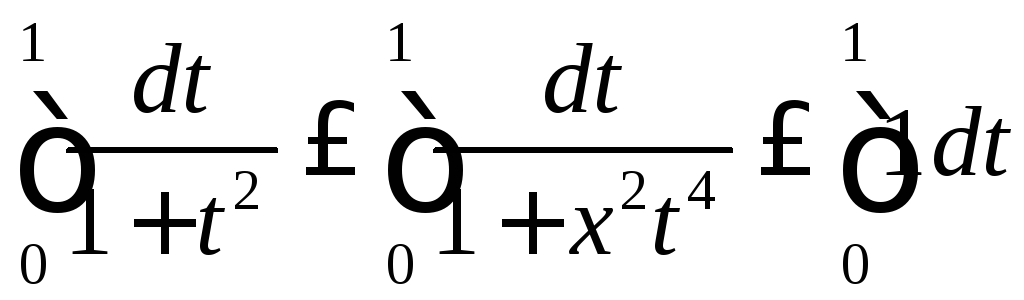 ,
,
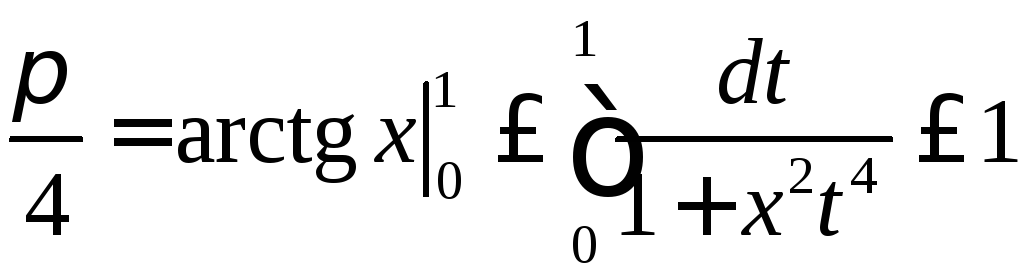 .
►
.
►
Убедиться, что функция
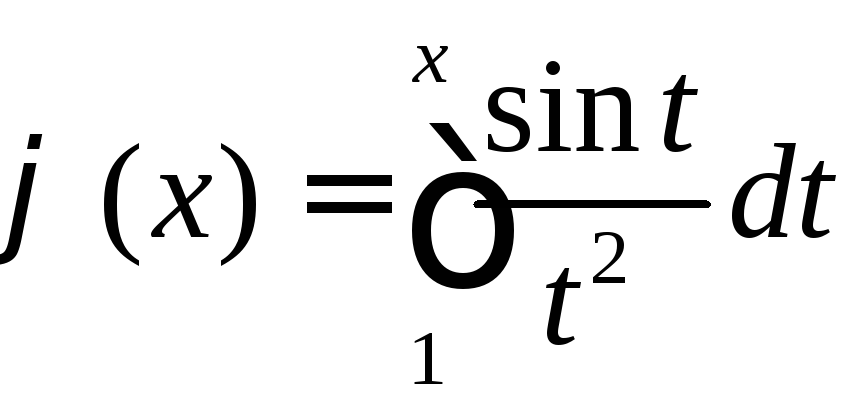 ограничена на промежутке
ограничена на промежутке .
.
◄ Пусть
![]() .
На основании свойства 4 определенного
интеграла
.
На основании свойства 4 определенного
интеграла
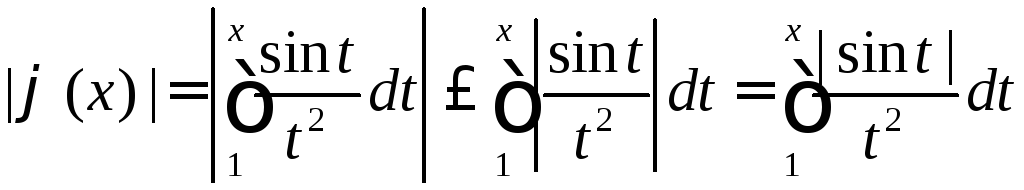 .
.
Так
как
![]() ,
то
,
то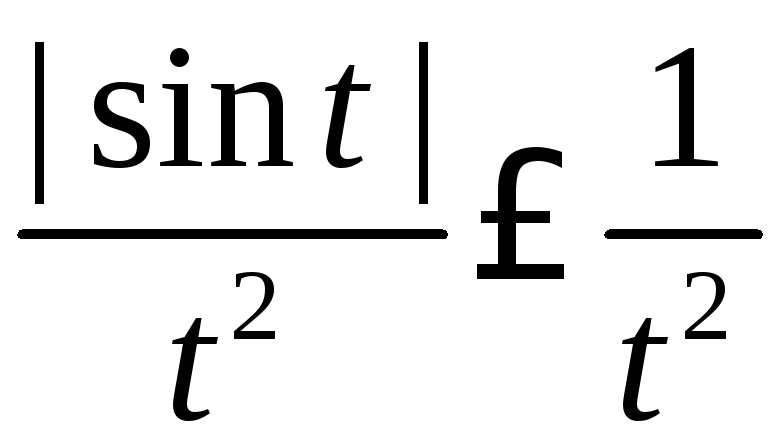 и, согласно свойству 3 определенного
интеграла,
и, согласно свойству 3 определенного
интеграла,
 .
.
Таким
образом,
![]()
![]() ,
то есть функция
,
то есть функция![]() ограничена на промежутке
ограничена на промежутке![]() .
►
.
►
Точка движется по прямой со скоростью
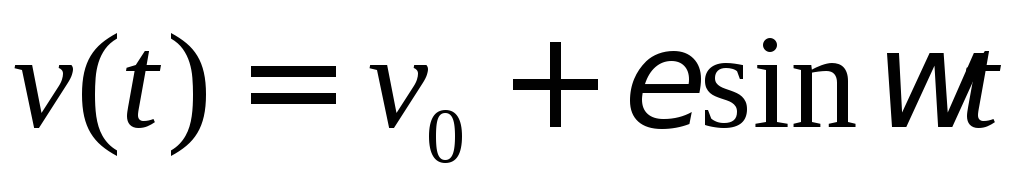 ,
периодически зависящей от времени.
Найти среднюю скорость за время
,
периодически зависящей от времени.
Найти среднюю скорость за время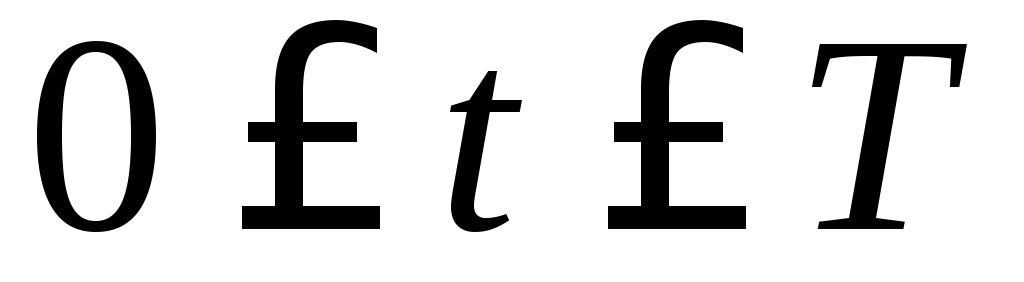 ,
где
,
где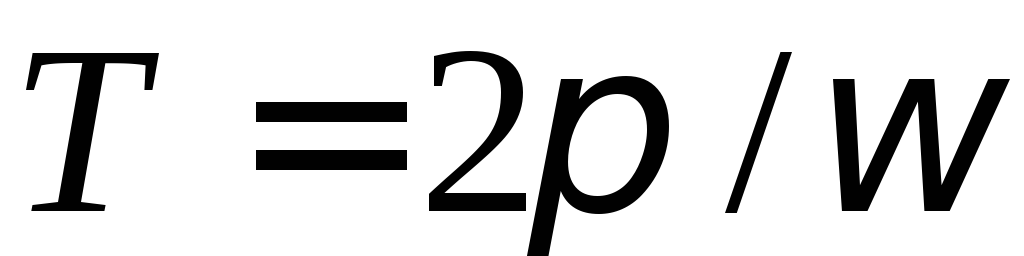 – период
– период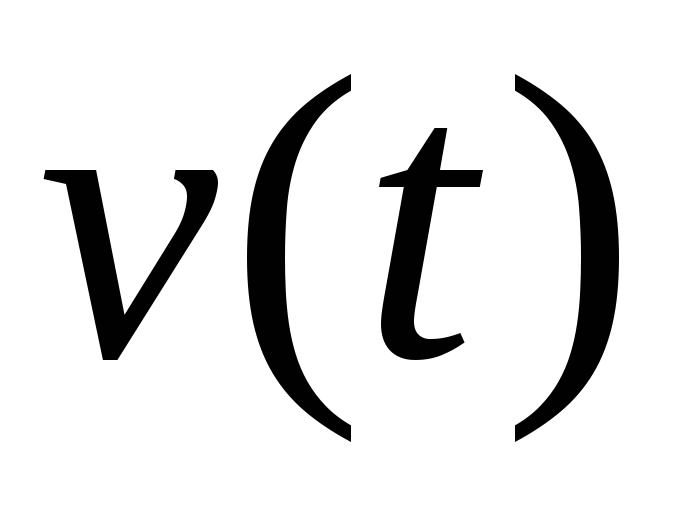 .
.
◄ Найдем
среднюю скорость как среднее значение
(мгновенной) скорости
![]() на отрезке
на отрезке![]() :
:
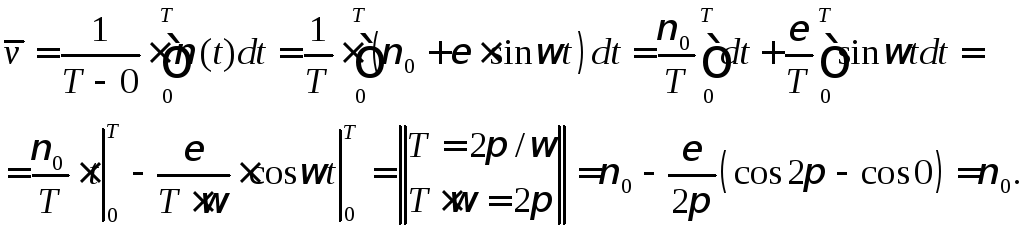
Замечание.
Так как
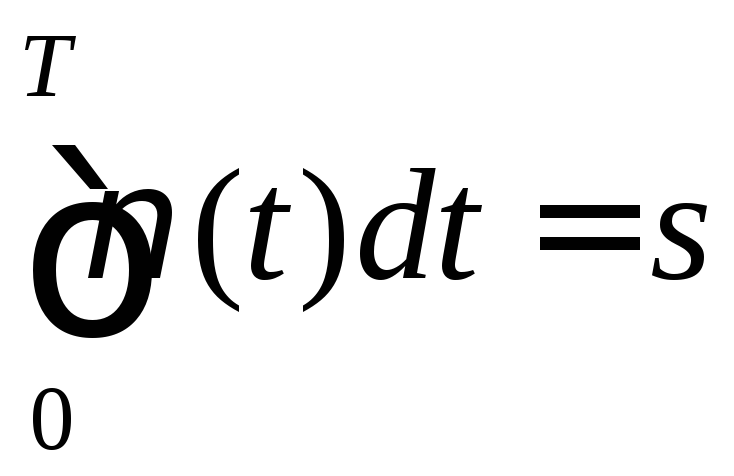 – путь, пройденный точкой за время от
– путь, пройденный точкой за время от![]() до
до![]() ,
то
,
то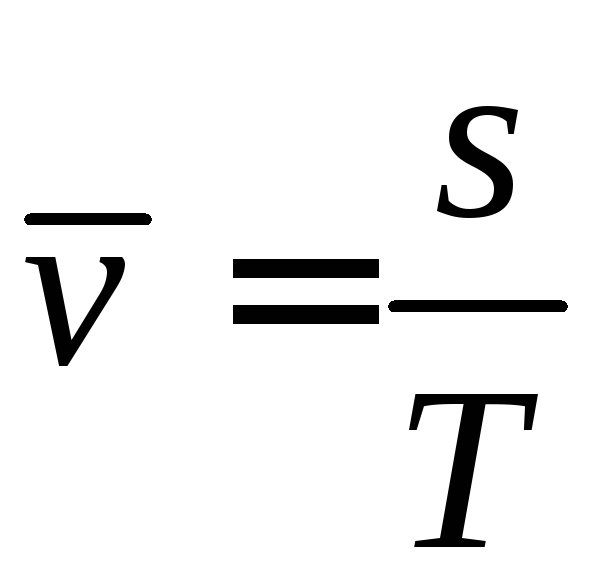 в полном согласии со “школьным”
определением средней скорости. ►
в полном согласии со “школьным”
определением средней скорости. ►
Найти производную функции
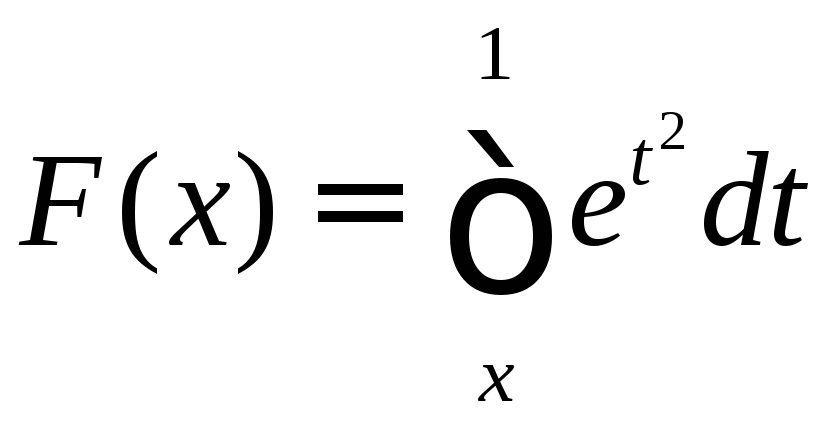 .
.
◄ По свойству 6 интеграла
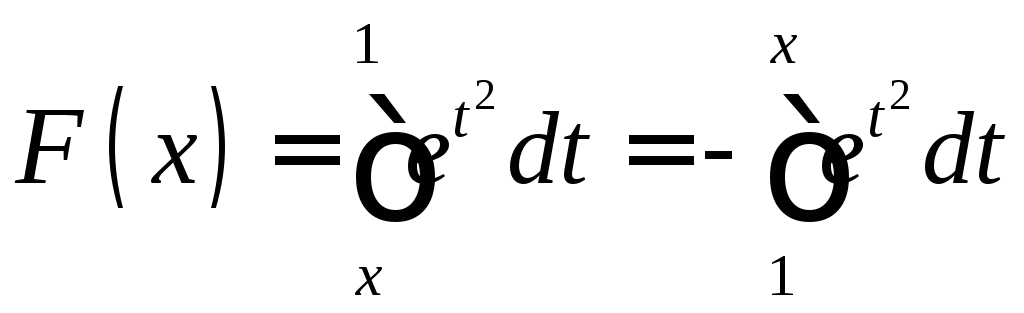 .
.
Теперь
по правилу дифференцирования интеграла
как функции верхнего предела (свойство
7) получаем
![]() .
►
.
►
Найти промежутки монотонности и экстремумы функции
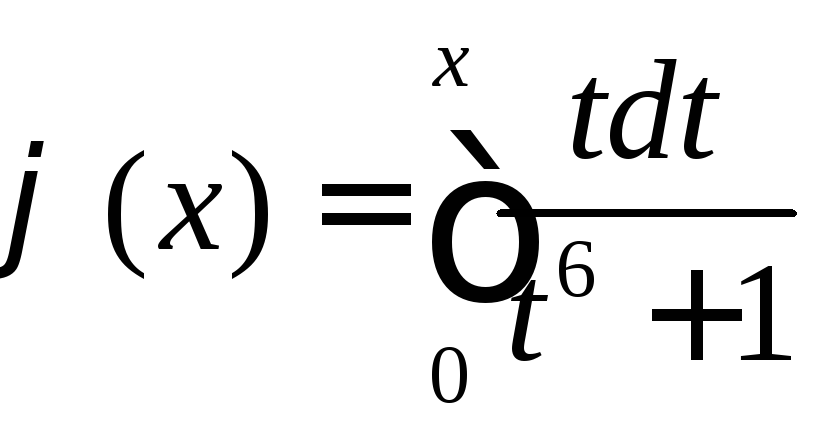 .
.
◄ а)
Найдем область определения
![]() функции. Так как функция
функции. Так как функция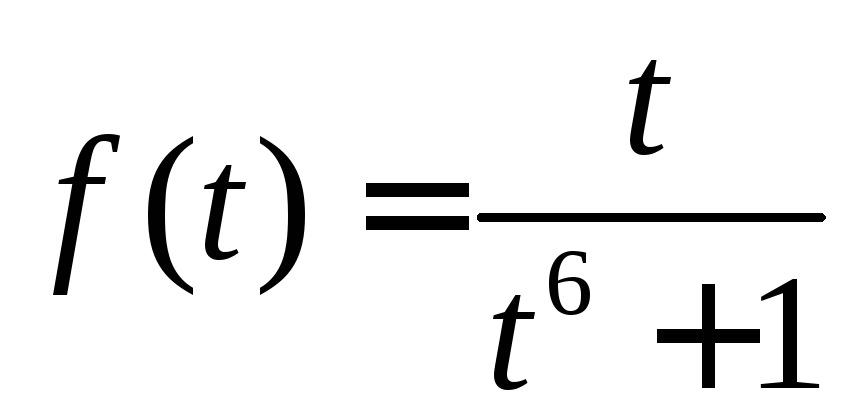 определена и непрерывна на всей числовой
прямой
определена и непрерывна на всей числовой
прямой![]() ,
то интеграл от неё
,
то интеграл от неё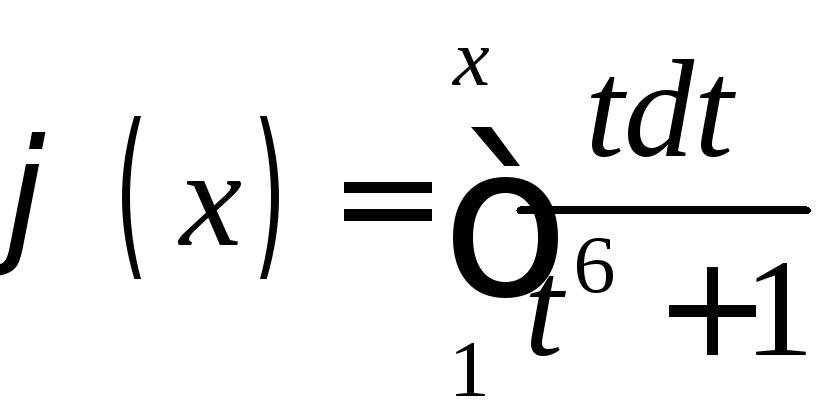 существует для любого
существует для любого![]() ,
т.е.
,
т.е.![]() .
.
б)
Найдем критические точки функции. По
правилу дифференцирования интеграла
как функции верхнего предела (свойство
7)
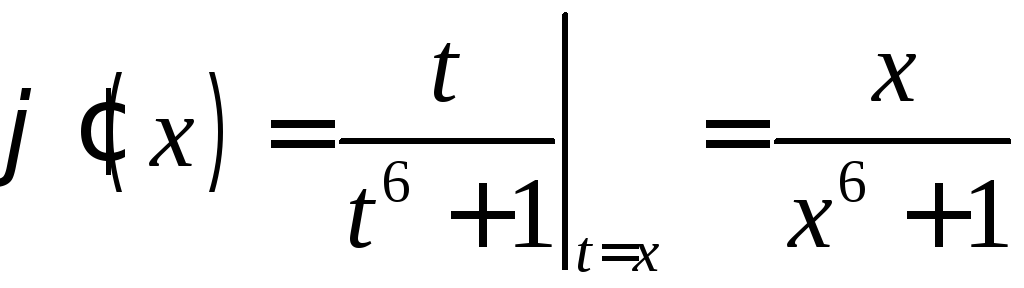 .
Поэтому
.
Поэтому![]() ,
то есть
,
то есть![]() – критическая точка.
– критическая точка.
в)
Разобьем
![]() критической точкой
критической точкой![]() на промежутки
на промежутки![]() и
и![]() и выясним знаки производной
и выясним знаки производной![]() на этих промежутках.
на этих промежутках.
![]()
![]() ,
поэтому
,
поэтому
![]() убывает на промежутке
убывает на промежутке![]() .
.
![]()
![]() ,
поэтому
,
поэтому
![]() возрастает на промежутке
возрастает на промежутке![]() .
г) В точке
.
г) В точке![]() функция имеет минимум,
функция имеет минимум,
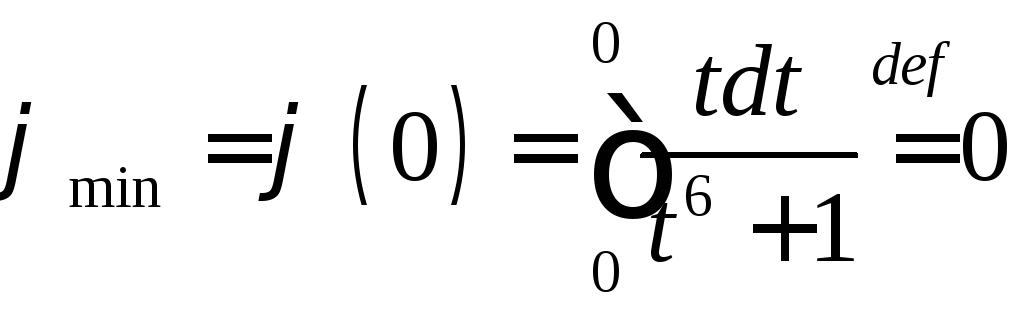 .
►
.
►
Задачи для самостоятельного решения
Вычислить
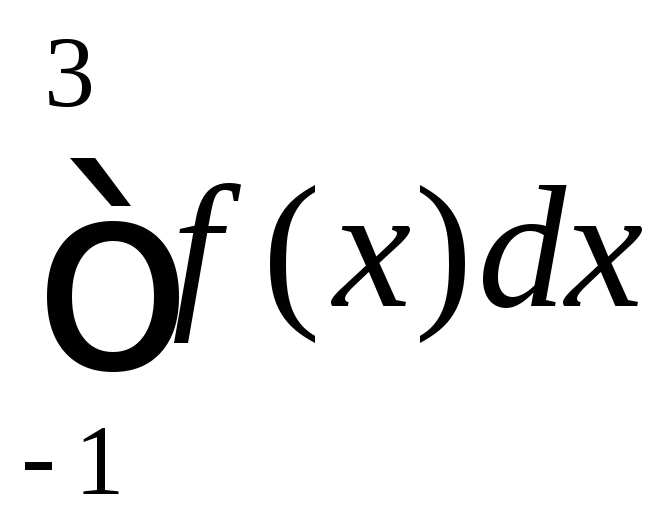 ,
если
,
если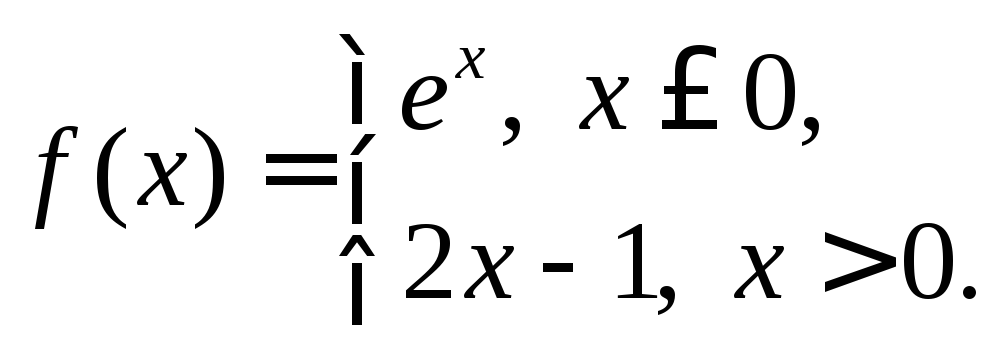
Вычислить
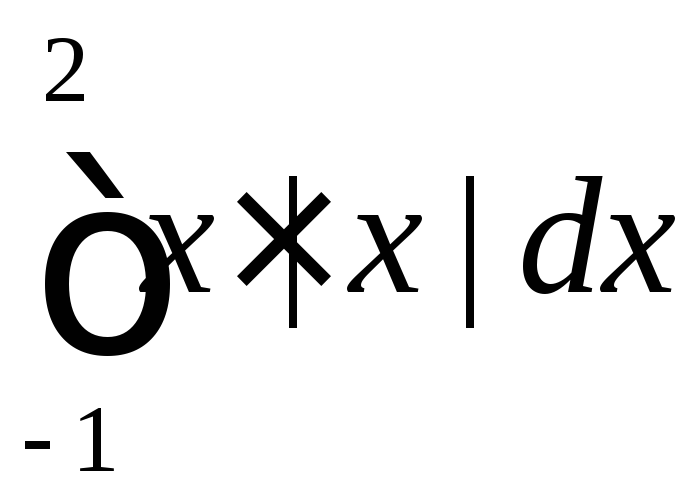 .
.Вычислить
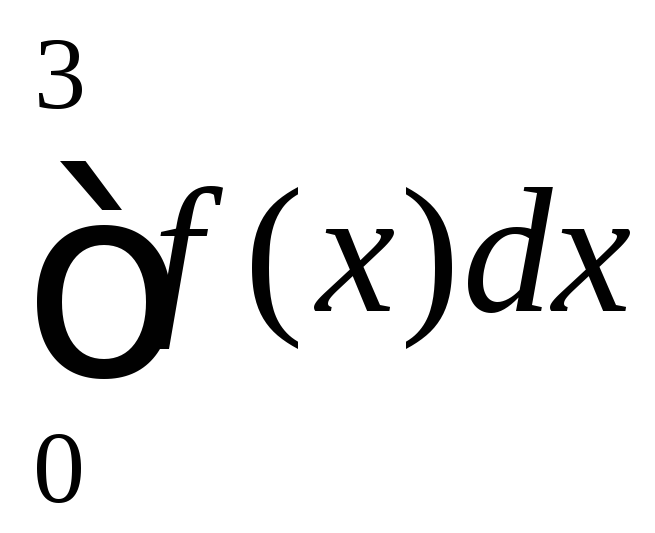 ,
если
,
если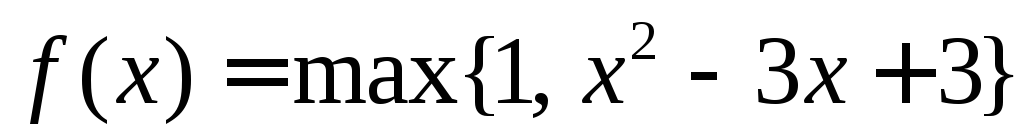 ,
то есть
,
то есть – наибольшее из чисел 1 и
– наибольшее из чисел 1 и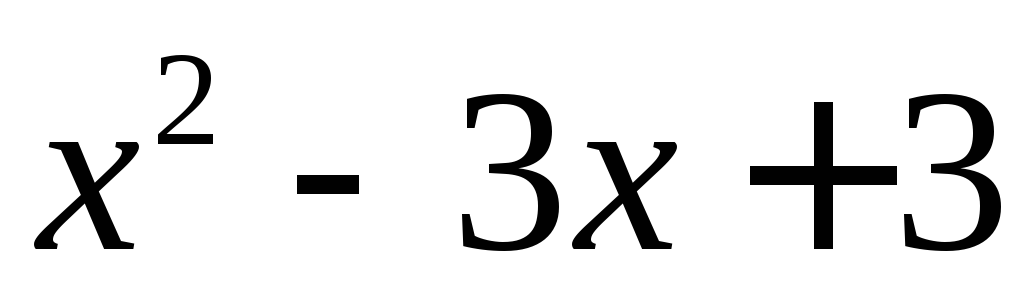 .
.Вычислить
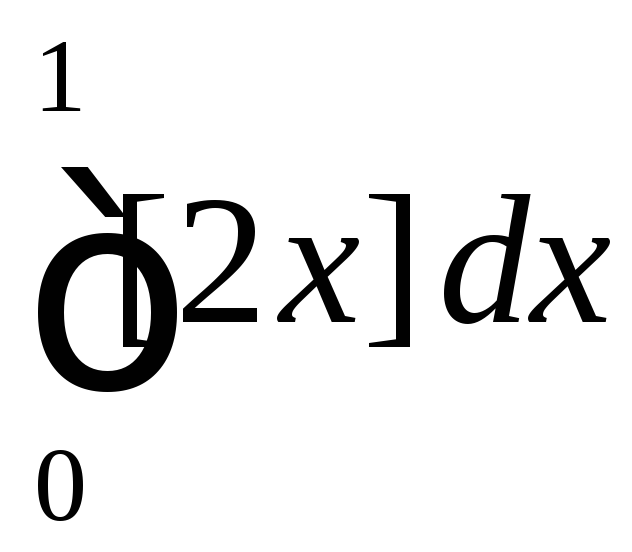 ,
где
,
где означает целую часть числа
означает целую часть числа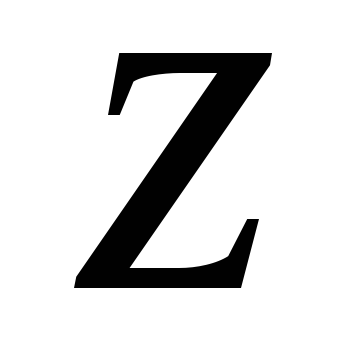 – наибольшее целое число
– наибольшее целое число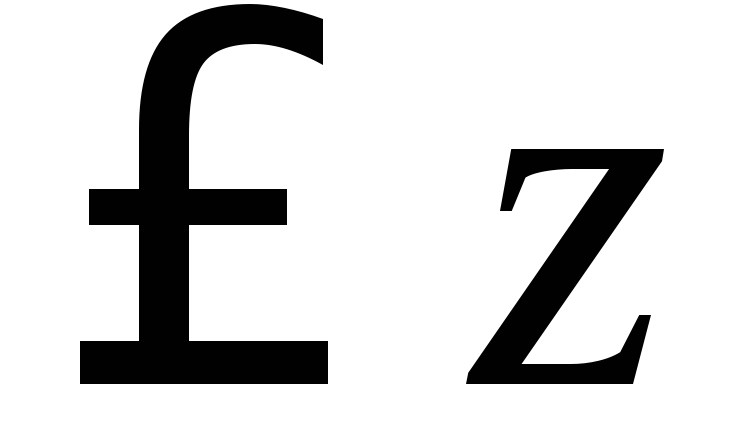 .
.Убедиться, что функция
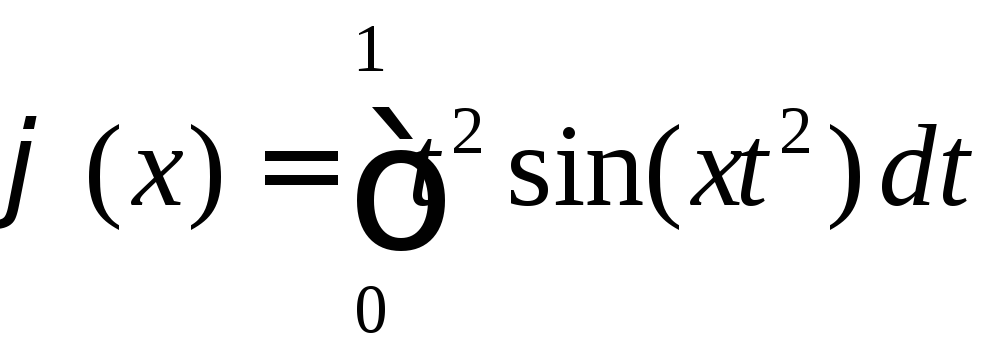 ограничена на всей числовой прямой
ограничена на всей числовой прямой .
.Доказать, что функция
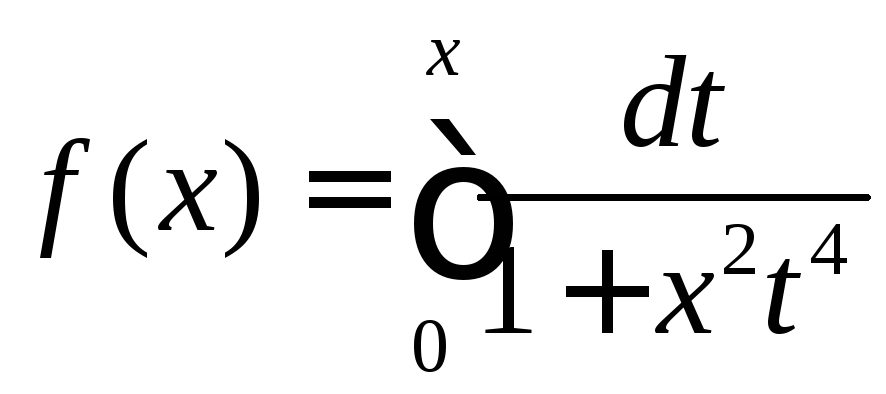 ограничена на
ограничена на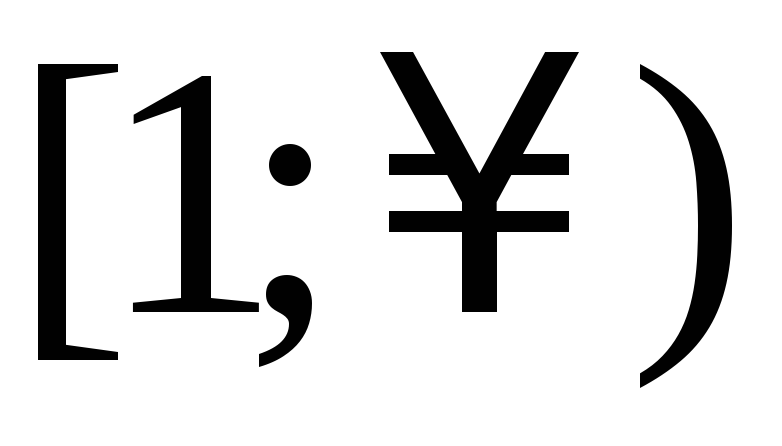 .Указание.
Доказать и использовать неравенство
.Указание.
Доказать и использовать неравенство
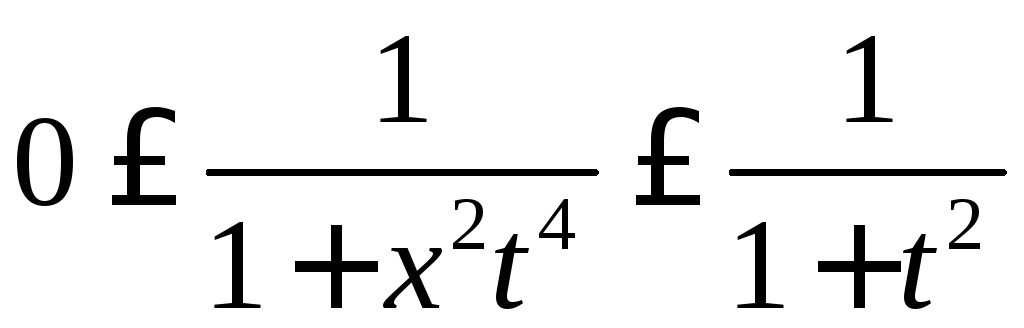 при
при
![]() .
.
Найти среднее значение функции
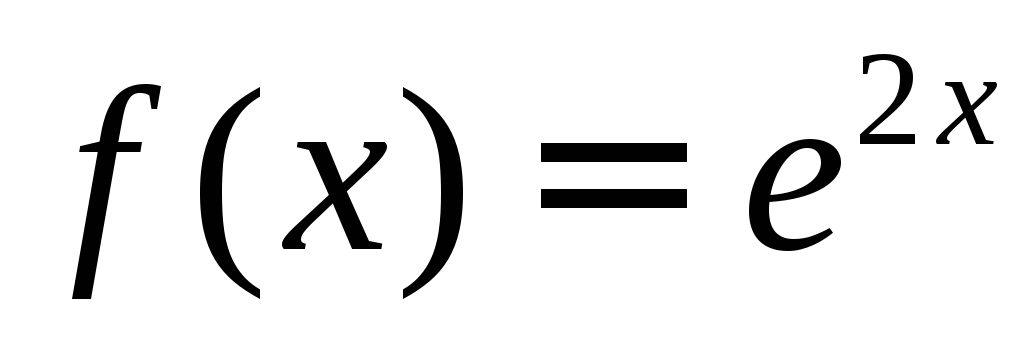 на отрезке
на отрезке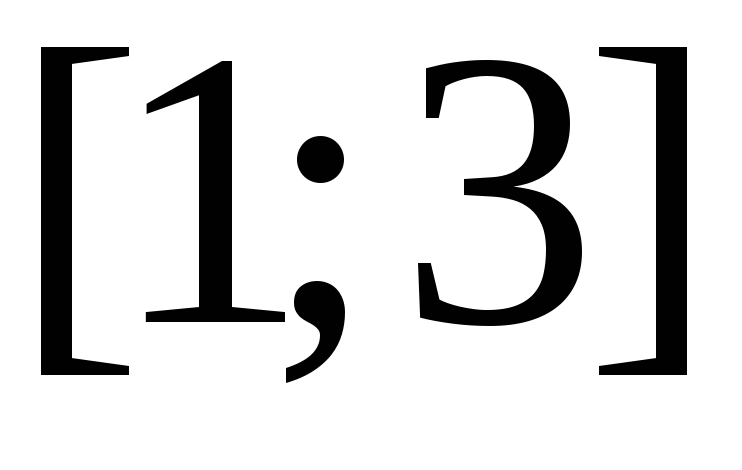 .
.Найти среднее значение функции
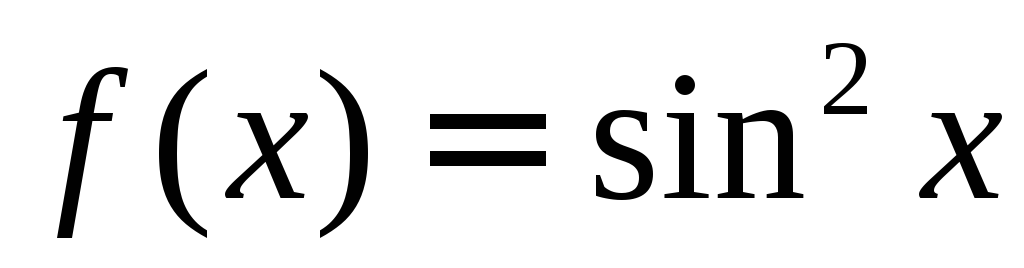 на отрезке
на отрезке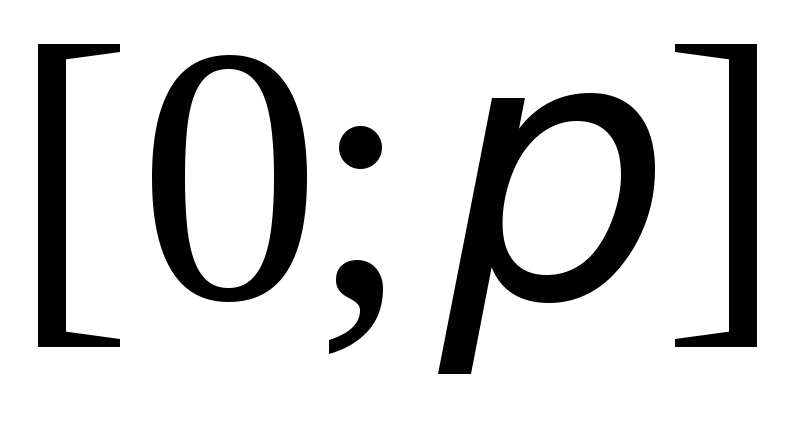 .
.Найти среднее значение силы переменного тока
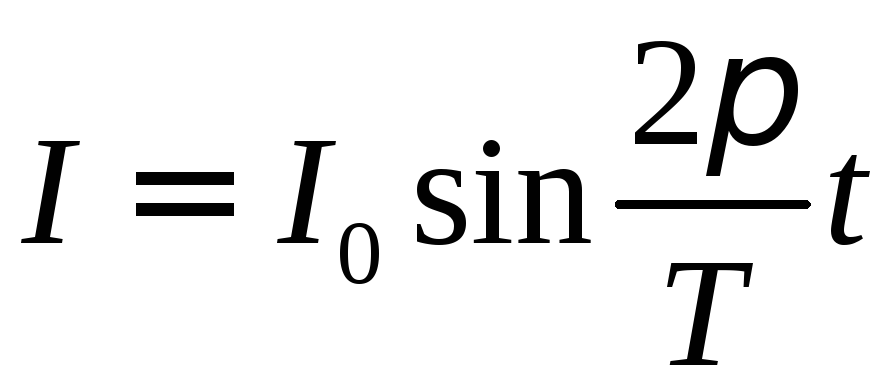 за полупериод
за полупериод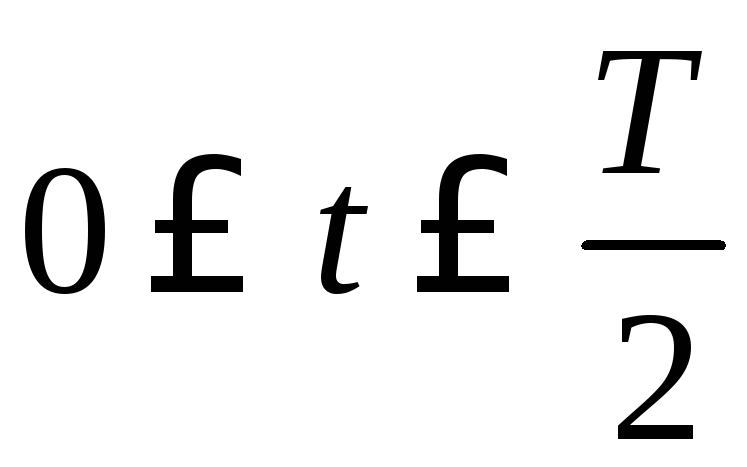 .
.Найти производную функции
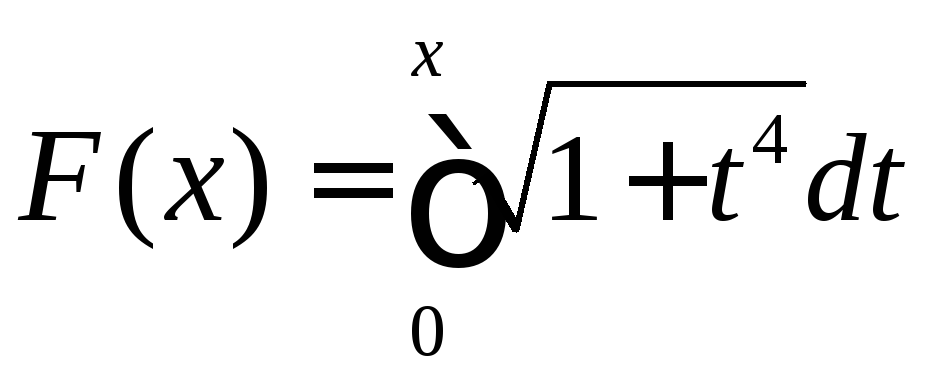 .
Убедиться, что функция возрастает на
.
Убедиться, что функция возрастает на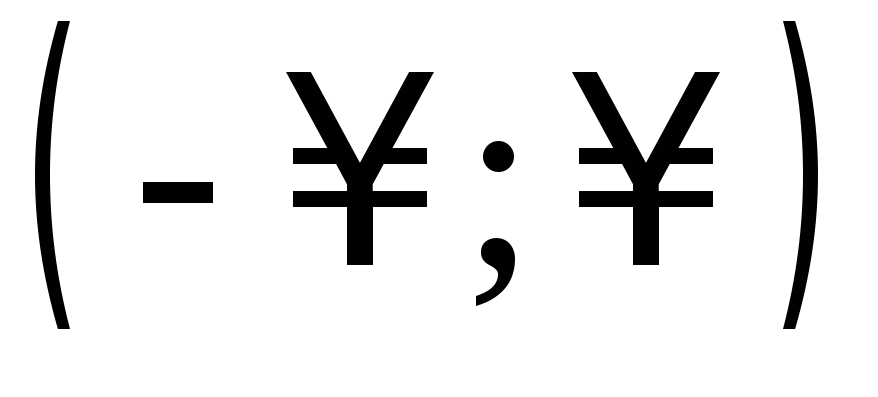 .
.Найти промежутки монотонности и экстремумы функции
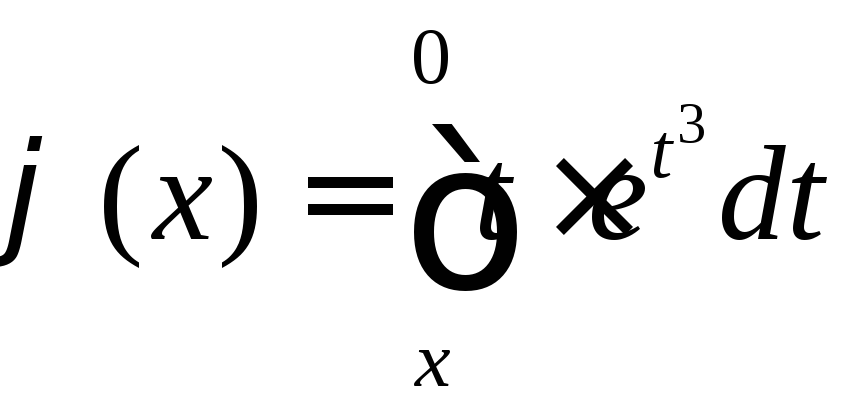 .
.Вычислить
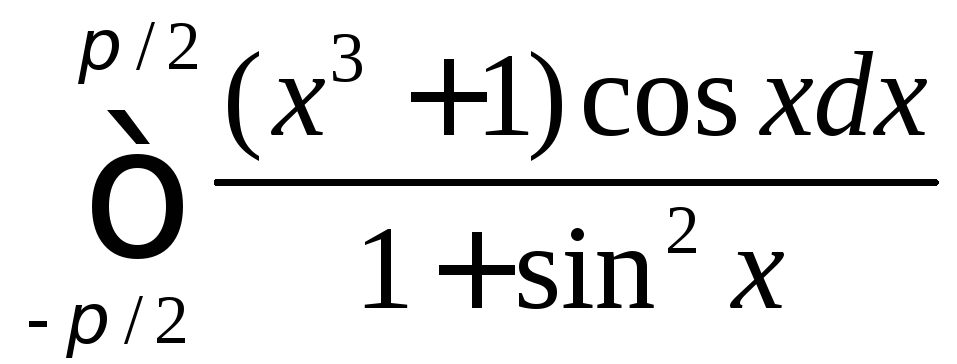 .
.
Указание. Подынтегральную функцию представить в виде суммы двух слагаемых, первое из которых является нечетной функцией, и воспользоваться свойством 8.
Доказать свойство 9, вычислив производную от интеграла
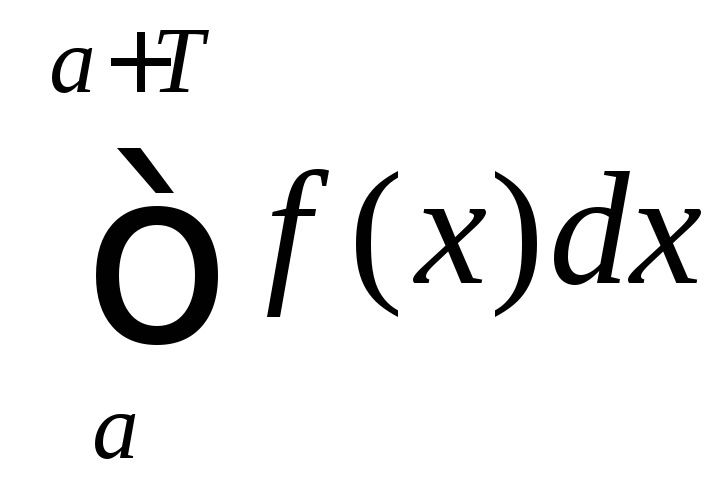 как функции аргумента
как функции аргумента
 .
.
Несобственные интегралы с бесконечными пределами
Сведения из теории
Если
функция
![]() определена и непрерывна на промежутке
определена и непрерывна на промежутке![]() ,
то
,
то
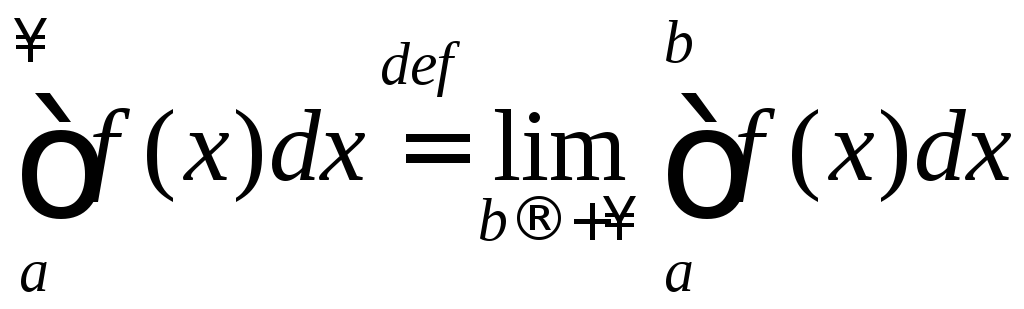 .
.
Если существует конечный предел в правой части формулы (7.1), то говорят, что несобственный интеграл сходится, если этот предел бесконечен или не существует, то несобственный интеграл расходится.
Если
![]() при
при![]() и несобственный интеграл сходится,
то он равен площади фигуры ограниченной
ось
и несобственный интеграл сходится,
то он равен площади фигуры ограниченной
ось![]() ,
графиком функции и прямой
,
графиком функции и прямой![]() (рис.
?)
(рис.
?)
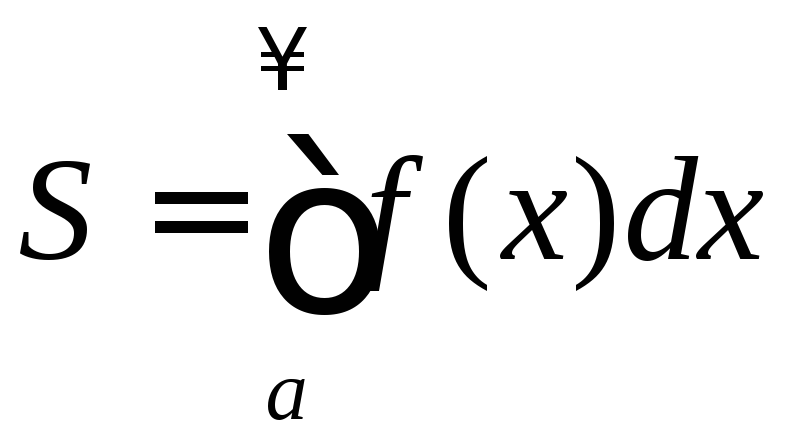 .
.
Аналогично
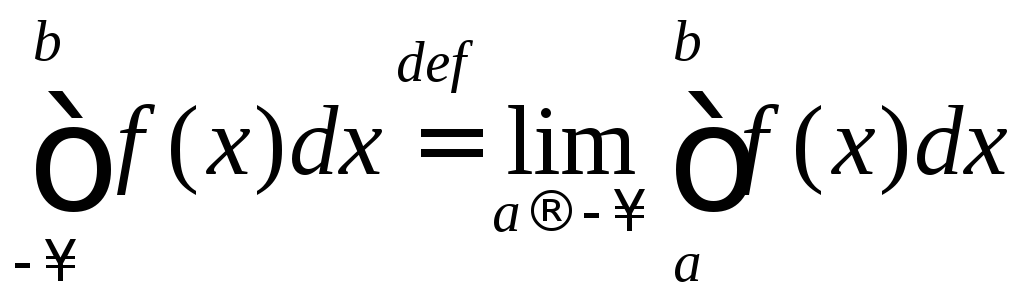 ,
,
если
![]() определена и непрерывна на промежутке
определена и непрерывна на промежутке![]() и
и
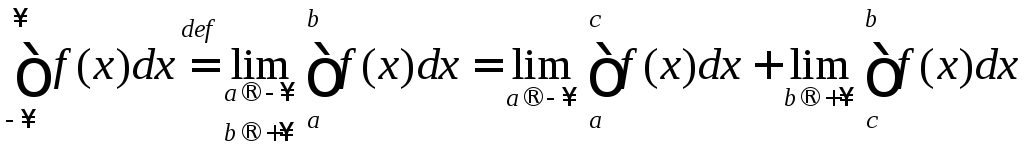 ,
,
если
![]() определена и непрерывна на промежутке
определена и непрерывна на промежутке![]() .
.
Ниже приводятся признаки сходимости несобственных интегралов вида . Для несобственных интегралов вида и они формулируются аналогично.
Обобщенная формула Ньютона-Лейбница.
Если
![]()
первообразная для
первообразная для
![]() и существует конечный предел
и существует конечный предел![]() ,
то интеграл (7.1) сходится и
,
то интеграл (7.1) сходится и
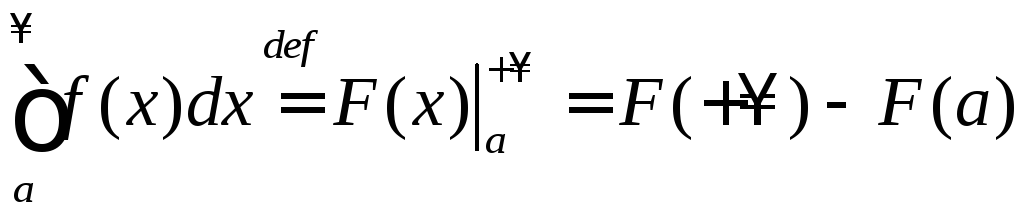 .
.
Если
же конечный
![]() не существует, то интеграл расходится.
не существует, то интеграл расходится.
2) Признак сравнения.
Пусть
![]()
![]() .
Если интеграл
.
Если интеграл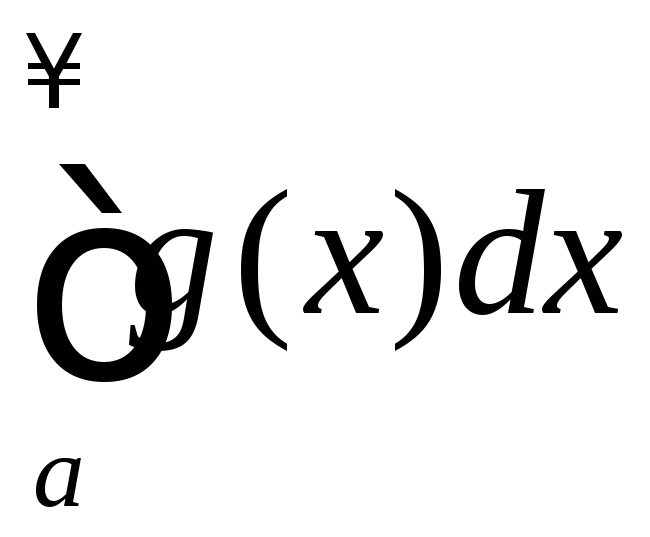 сходится, то сходится и интеграл
сходится, то сходится и интеграл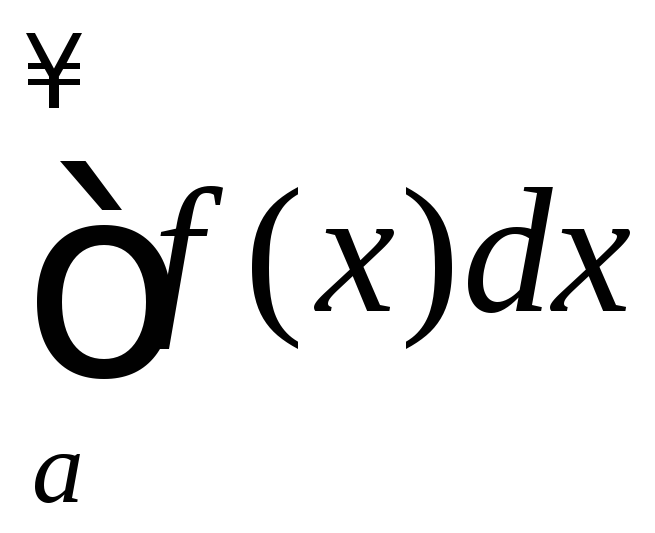 .
Если интеграл
.
Если интеграл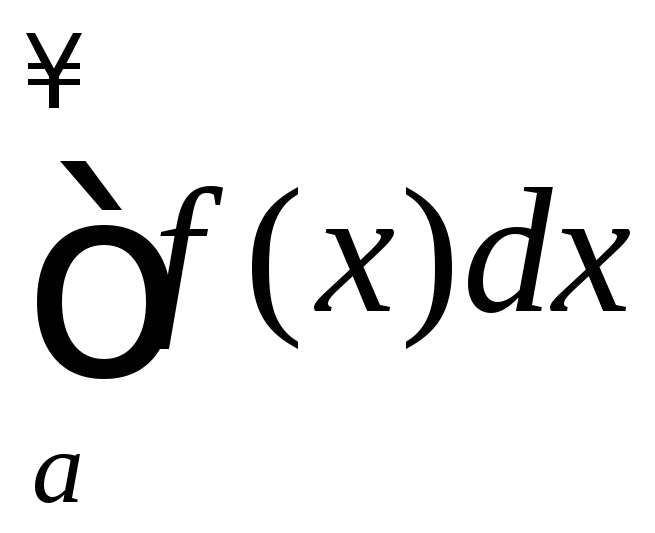 расходится, то расходится и интеграл
расходится, то расходится и интеграл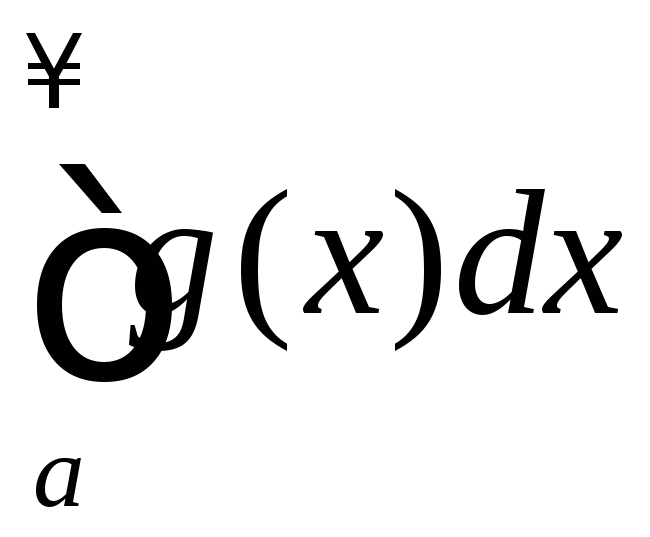 .
.
3) Предельный признак сравнения.
Если
![]() и
и![]() положительные функции одного порядка
при
положительные функции одного порядка
при![]() ,
то есть
,
то есть![]() ,
где
,
где![]() (
(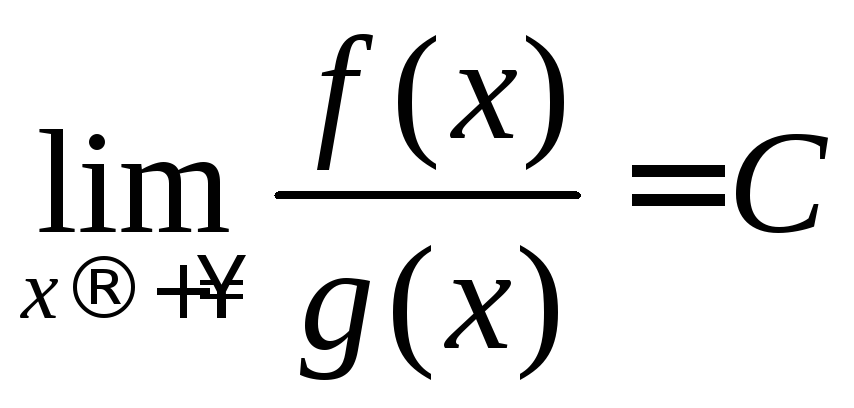 ),
то интегралы
),
то интегралы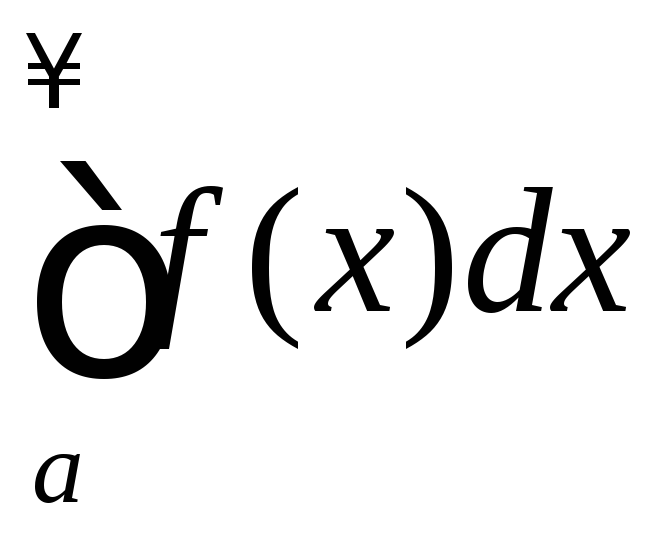 и
и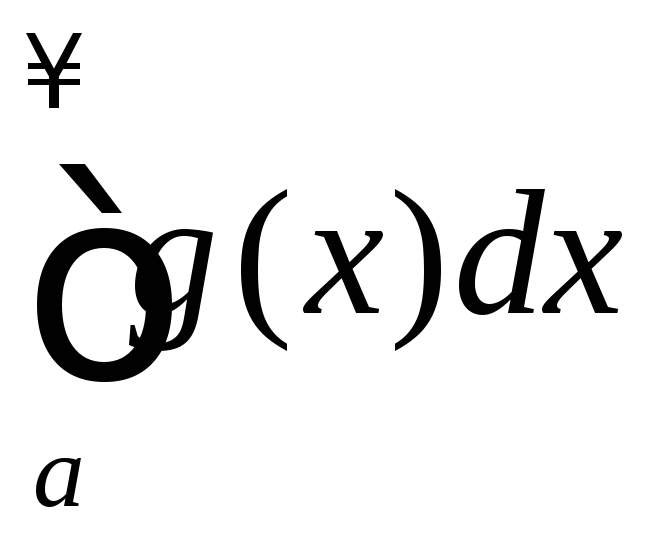 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Замечание. При использовании признаков сравнения полезно иметь ввиду интеграл
![]() (
(![]() ),
),
сходящийся
при
![]() и расходящийся при
и расходящийся при![]() .
.
4) Абсолютная сходимость.
Если
сходится интеграл
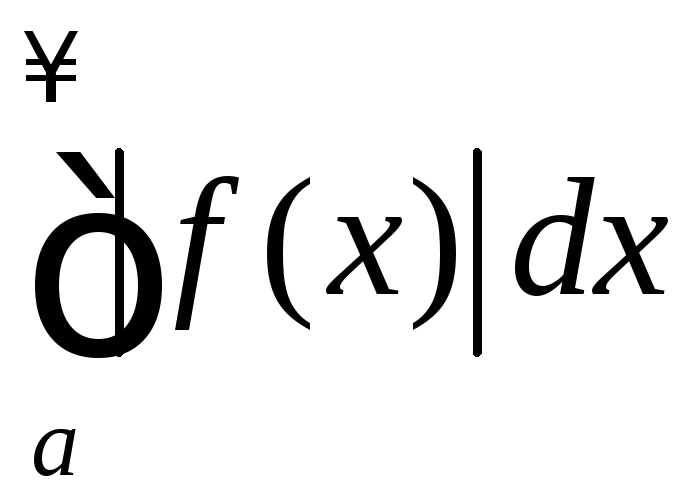 ,
то сходится и интеграл
,
то сходится и интеграл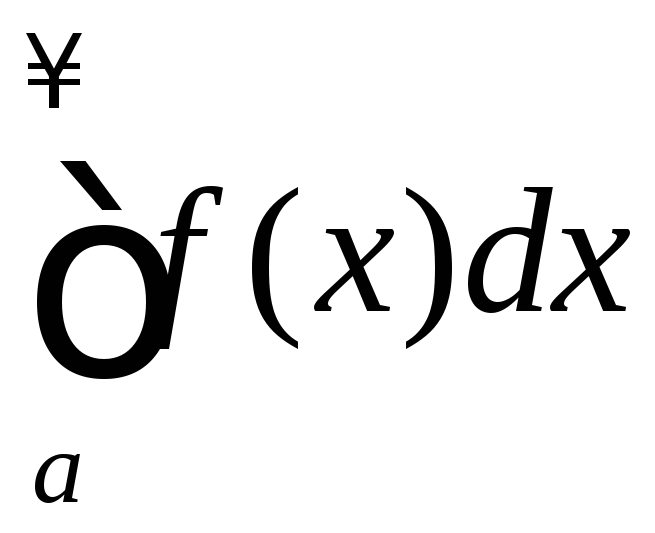 ,
(в этом случае говорят, что онсходится
абсолютно).
,
(в этом случае говорят, что онсходится
абсолютно).
Примеры решения задач
В задачах 11.2.1-11.2.2 вычислить несобственные интегралы (или доказать их расходимость) а) по определению, б) по формуле Ньютона-Лейбница .
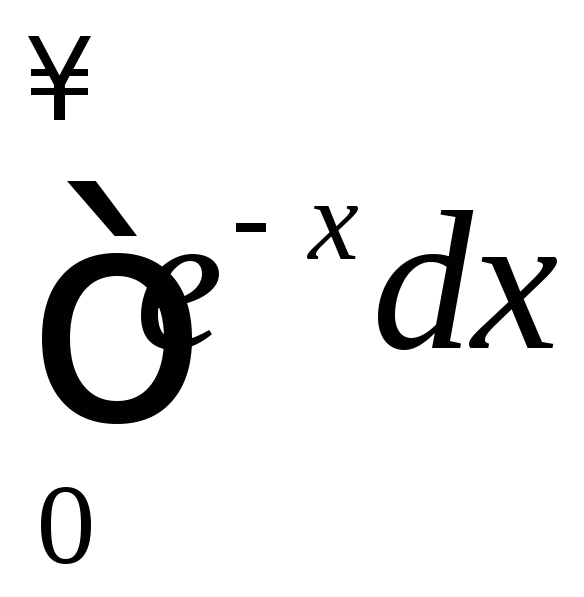 .
.
а)
◄
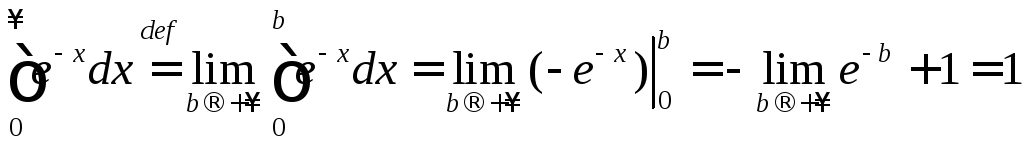 .
.
Интеграл сходится. ►
б)
◄
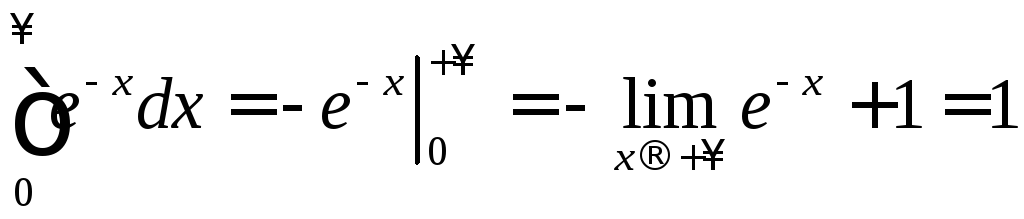 ►
►
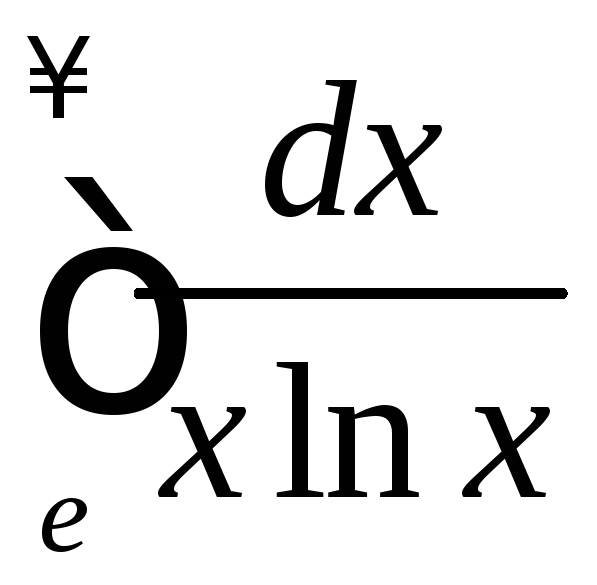 .
.
а)
◄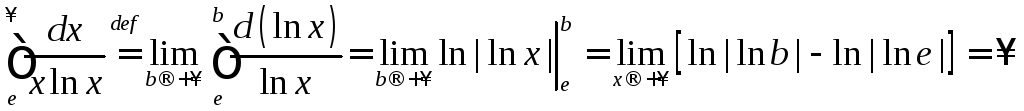 .
Интеграл расходится. ►
.
Интеграл расходится. ►
б)
◄
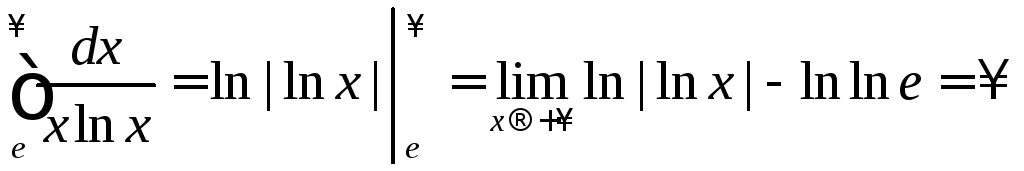 ►
►
Найти площадь
 фигуры, заданной неравенствами
фигуры, заданной неравенствами
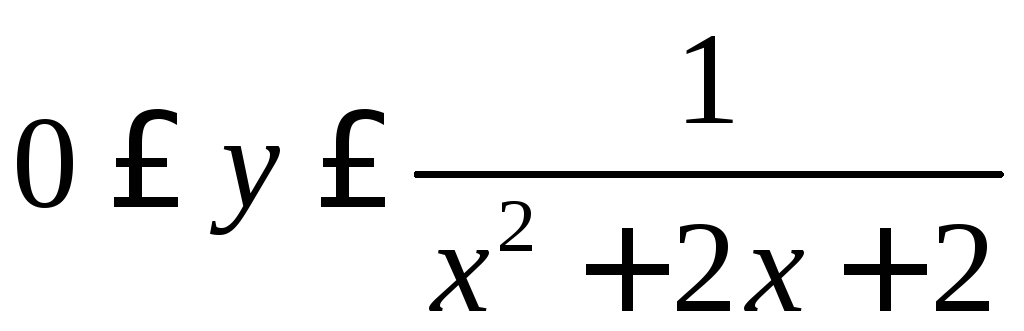 (рис.
).
(рис.
).
◄
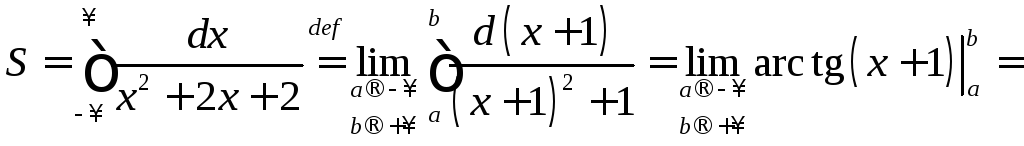
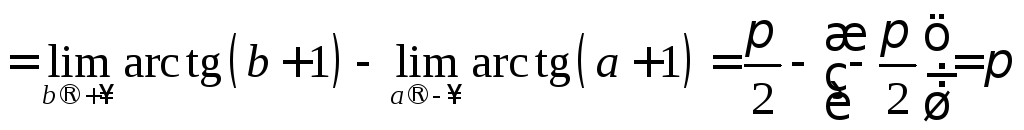 .
►
.
►
Исследовать сходимость несобственного интеграла
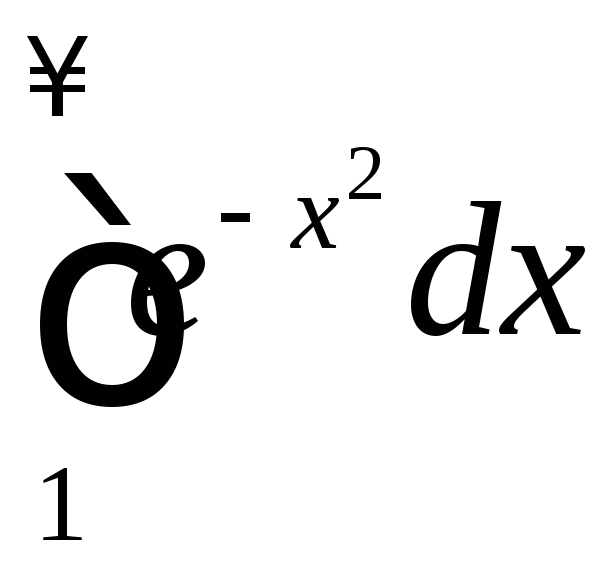 .
.
◄ Применим
признак сравнения. При
![]()
![]() и
и![]() .
Интеграл
.
Интеграл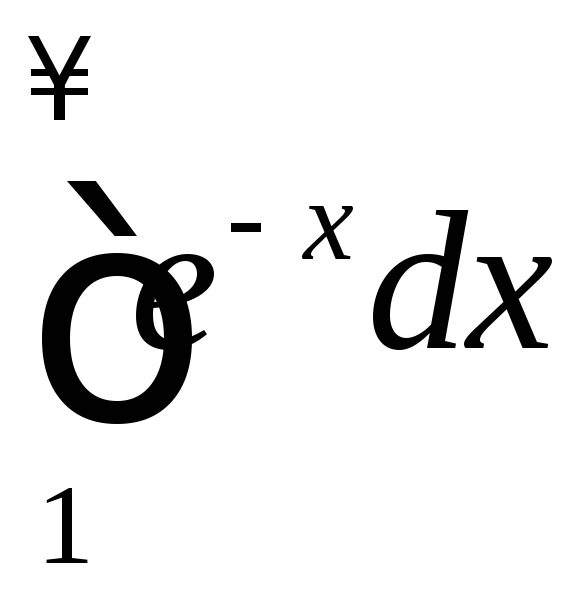 сходится (см. задачу11.2.1),
поэтому сходится и интеграл
сходится (см. задачу11.2.1),
поэтому сходится и интеграл
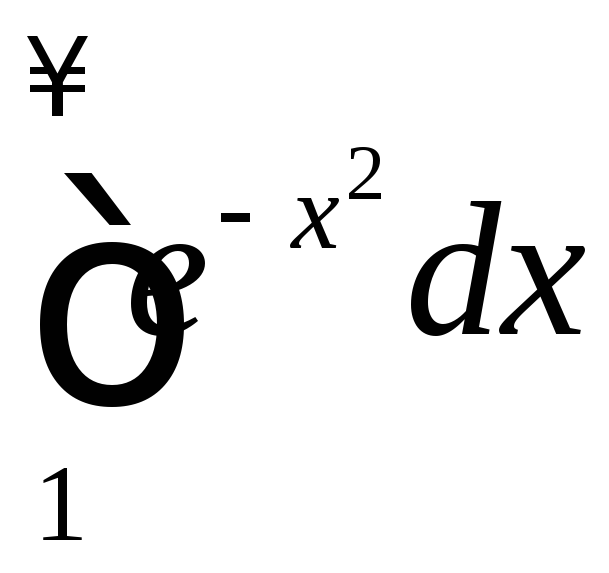 .
►
.
►
Исследовать сходимость несобственного интеграла
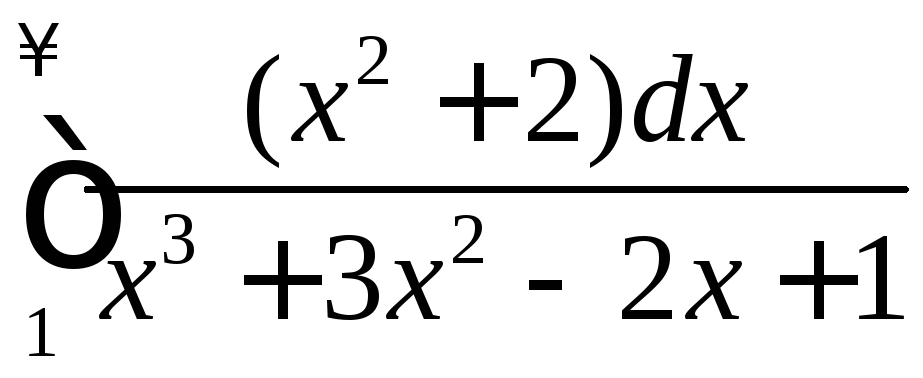 .
.
◄ Применим
предельный признак сравнения. В числителе
и знаменателе дроби
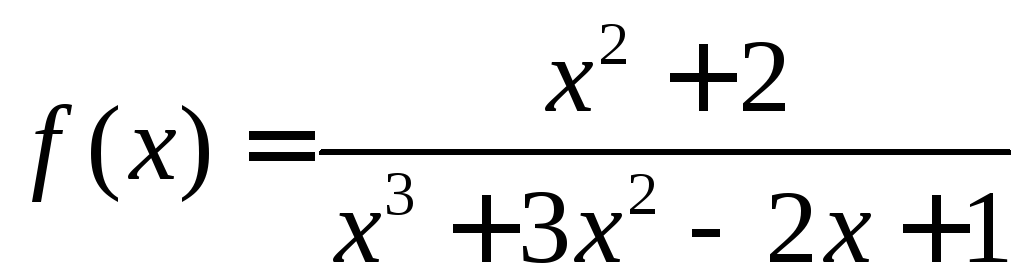 сохраним только слагаемые с наибольшими
степенями – “главные” при
сохраним только слагаемые с наибольшими
степенями – “главные” при![]() .
Получим функцию
.
Получим функцию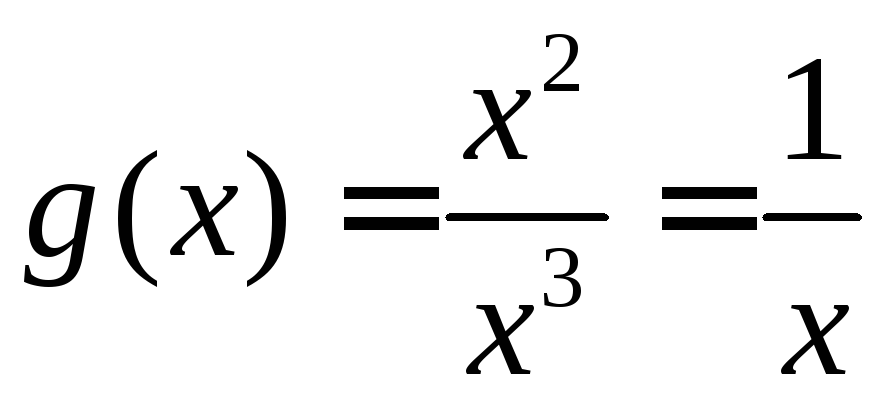 ,
эквивалентную
,
эквивалентную![]() :
:![]() .
Это можно проверить и непосредственно
по определению эквивалентности:
.
Это можно проверить и непосредственно
по определению эквивалентности: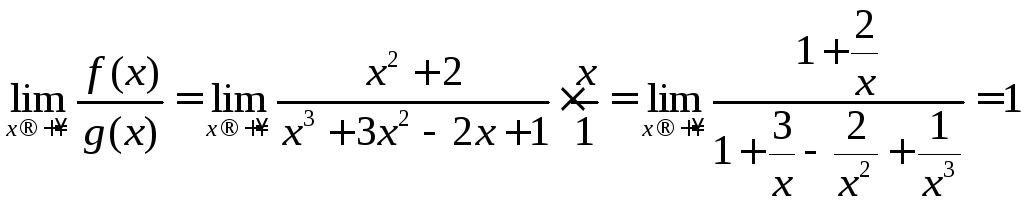 .
.
Так
как
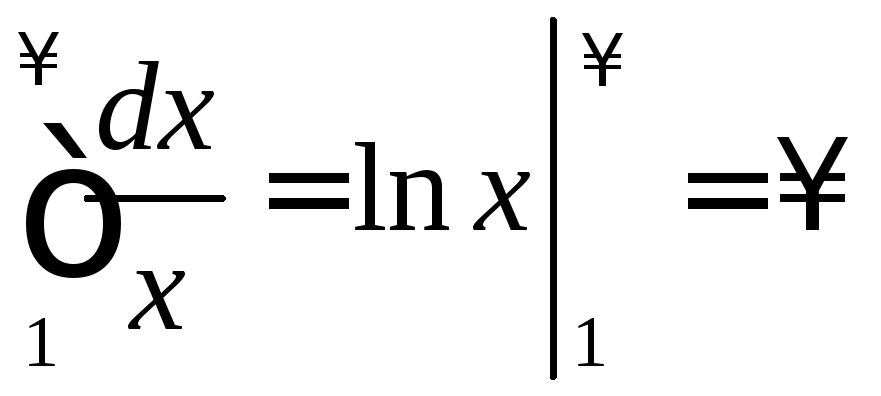
расходится, то расходится и интеграл
расходится, то расходится и интеграл
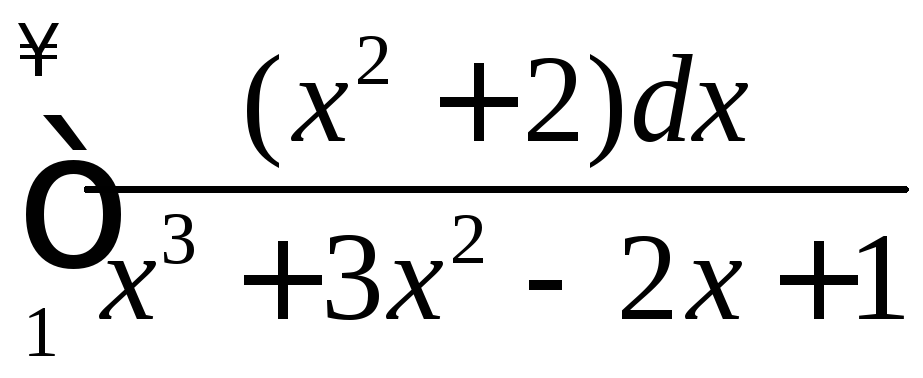 .►
.►
Исследовать сходимость несобственного интеграла
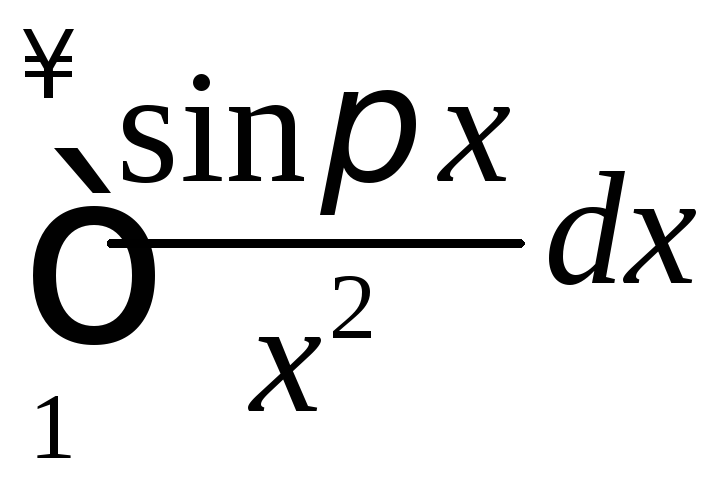 .
.
◄ Так
как
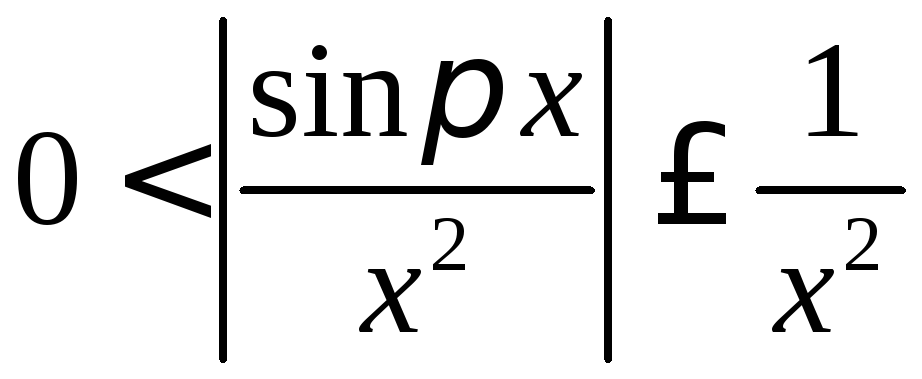 ,
а интеграл
,
а интеграл сходится, то по признаку сравнения
сходится и интеграл
сходится, то по признаку сравнения
сходится и интеграл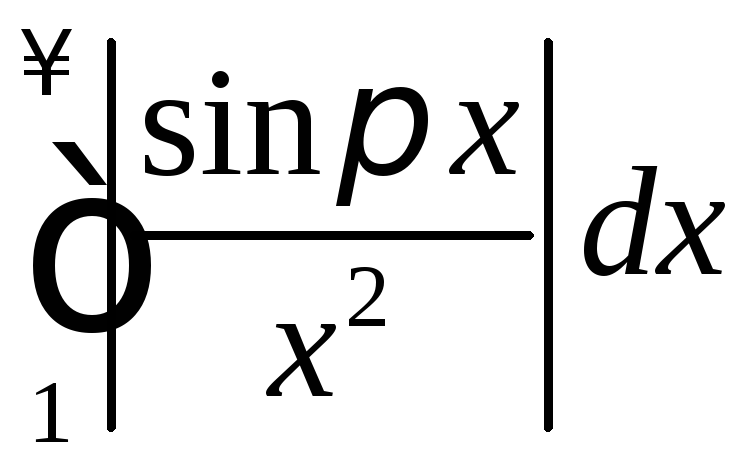 .
Но это означает, что
.
Но это означает, что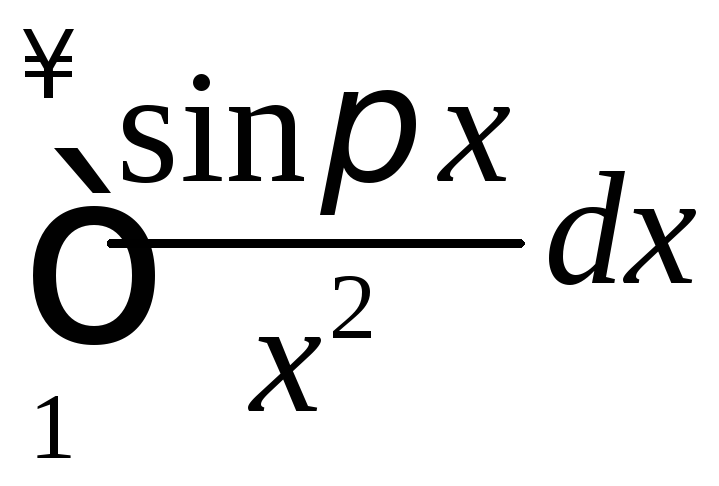 сходится абсолютно. ►
сходится абсолютно. ►
Замечание.
В примерах 11.1.5
и 11.1.6
мы могли не вычислять интегралы
![]() и
и![]() ,
а просто сослаться на то, что они являются
частными случаями стандартного интеграла
при
,
а просто сослаться на то, что они являются
частными случаями стандартного интеграла
при![]() (расходящегося) и
(расходящегося) и![]() (сходящегося).
(сходящегося).
Задачи для самостоятельного решения
В задачах 11.3.1-11.3.8 вычислить несобственные интегралы (или доказать их расходимость) а) по определению, б) по формуле Ньютона-Лейбница .
В задачах 11.3.7-11.3.12 исследовать сходимость несобственных интегралов.
-
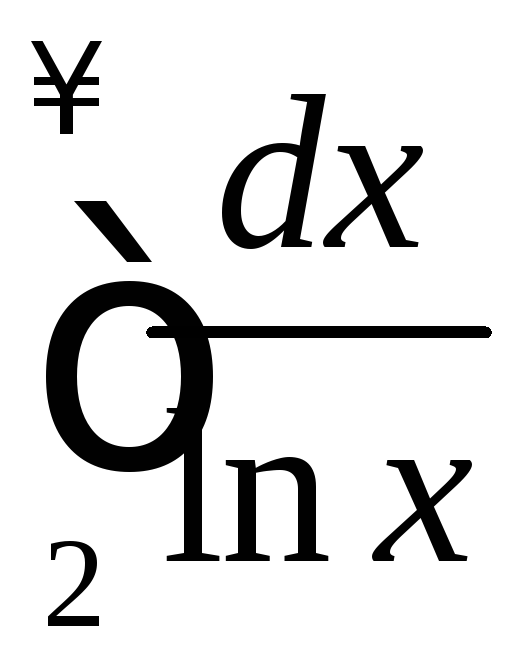 .
.
Указание.
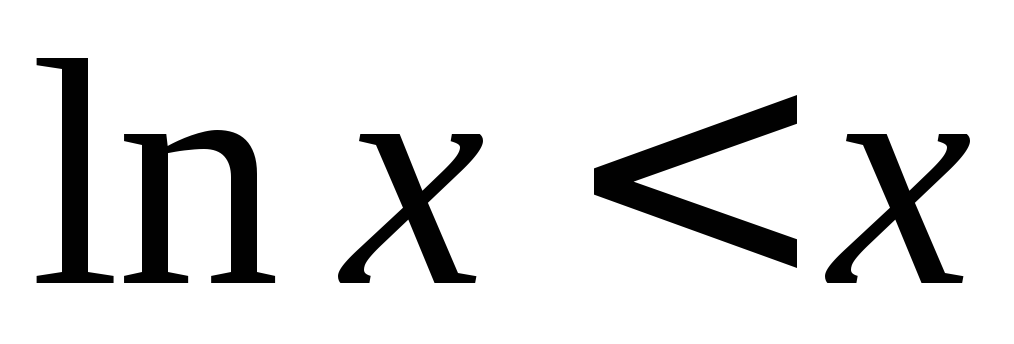 при
при .
.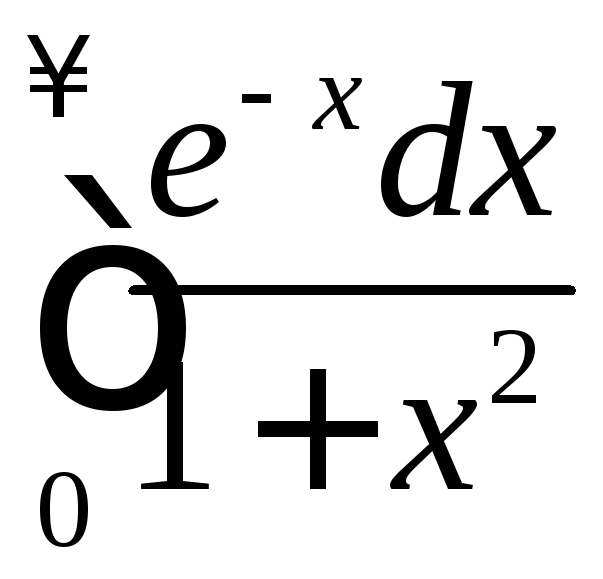 .
.
Указание.
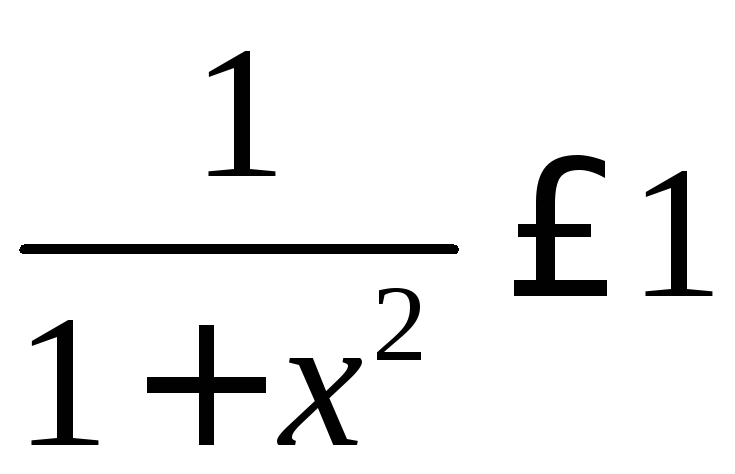 .
.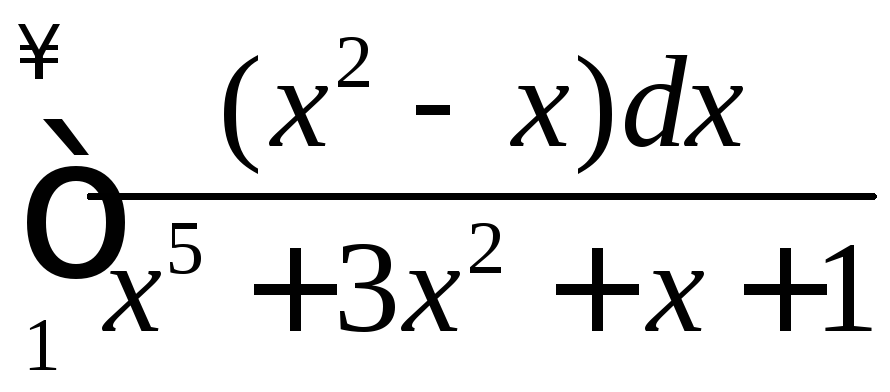 .
.
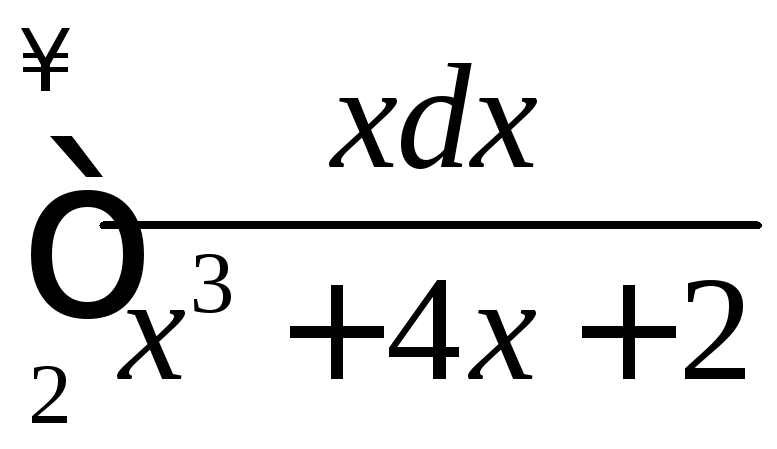 .
.
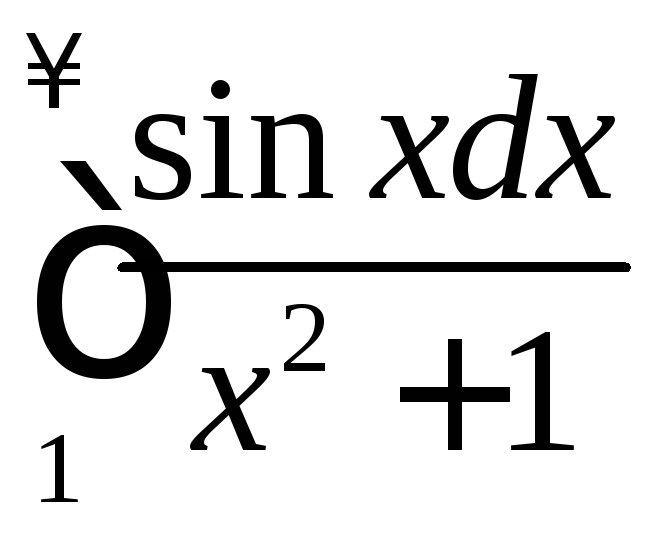 .
.
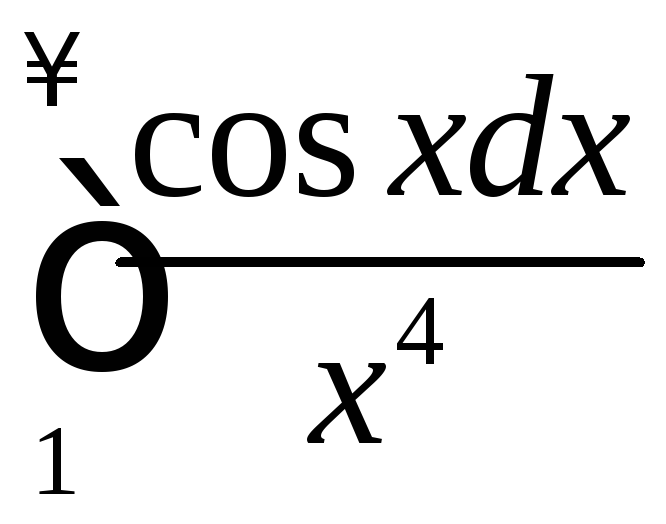 .
.