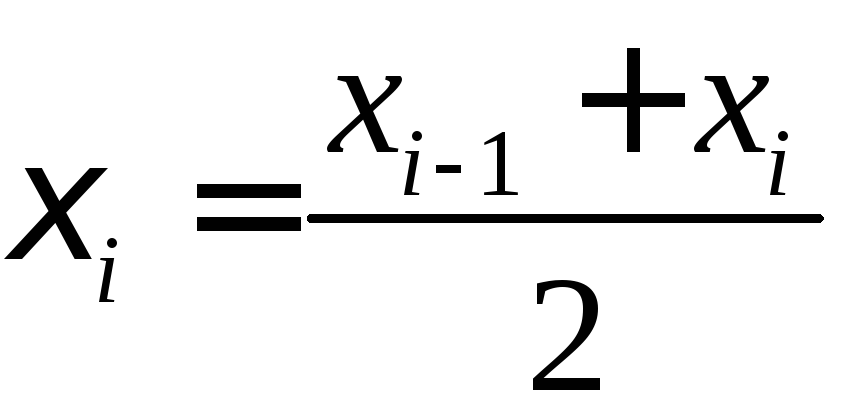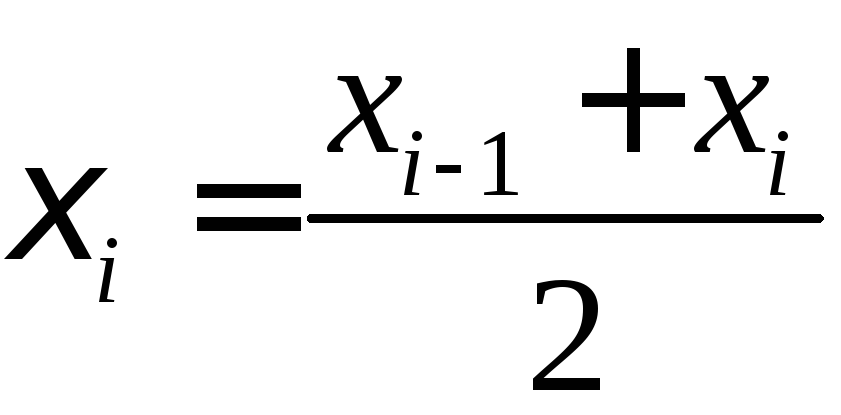- •Неопределенный интеграл
- •План 2009
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Интегрирование по частям
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Простейшие интегралы,
- •Интегрирование неправильных рациональных дробей
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Тригонометрические интегралы
- •Сведения из теории
- •Интегралы вида
- •Интегралы вида ,
- •Задачи для самостоятельного решения
- •Интегрирование некоторых иррациональных функций
- •Формула Ньютона-Лейбница. Интегрирование по частям в определенном интеграле. Замена переменной в определенном интеграле
- •Свойства определенного интеграла
- •Примеры решения задач
- •Несобственные интегралы с бесконечными пределами
- •Сведения из теории
- •Несобственные интегралы от неограниченных функций
- •Площадь плоской фигуры. Объем тела вращения
- •Полярные координаты. Вычисление площадей в полярных координатах
- •Длина дуги кривой. Площадь поверхности вращения
- •Библиографический список
Интегралы вида ,
где хотя бы одно из чисел m или n нечетное целое число
Пусть,
например,
![]() –
нечетно. Тогда
–
нечетно. Тогда
![]()
![]() (замена
(замена
![]() )
)![]() ,
,
то есть интеграл сводится к сумме табличных интегралов от степеней.
Интегралы вида
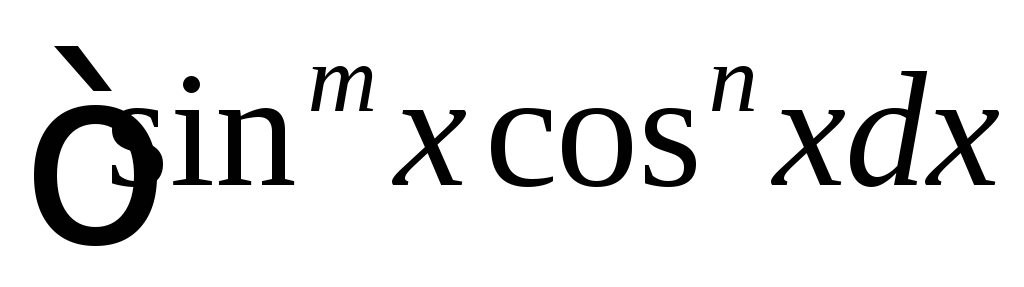 ,
,
где m и n четные целые числа
Если m и n четные целые положительные числа, то используем формулы понижения степени
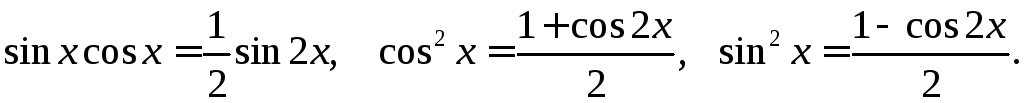
Интегралы от произведений синусов и косинусов
различных аргументов
Для их вычисления используются тригонометрические формулы
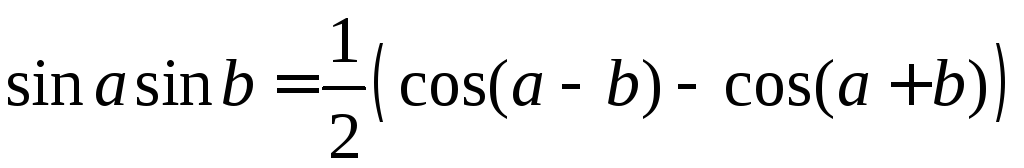 .
.
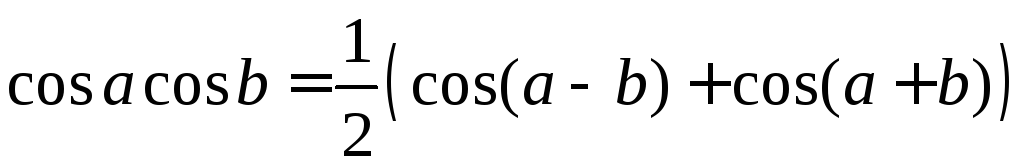 .
.
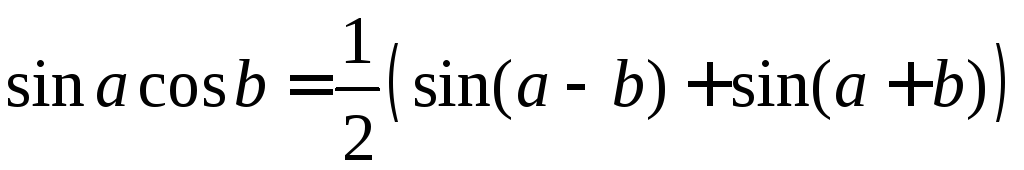 .
.
Примеры решения задач
Вычислить
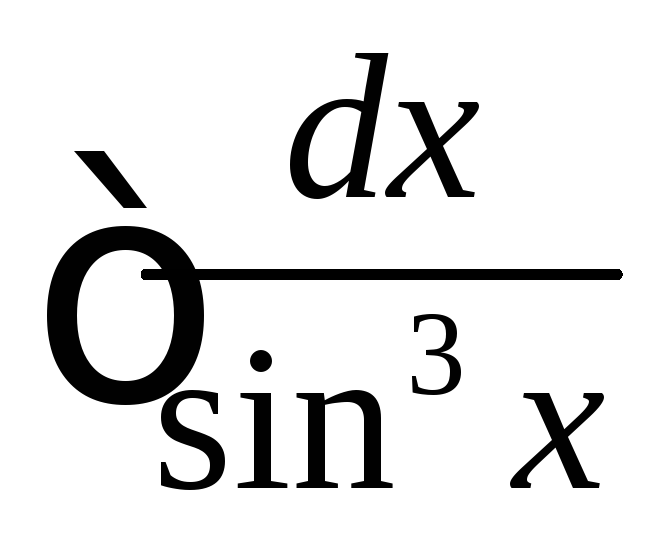 .
.
◄ Сделаем
универсальную подстановку
![]() .
Используя формулы , получаем
.
Используя формулы , получаем
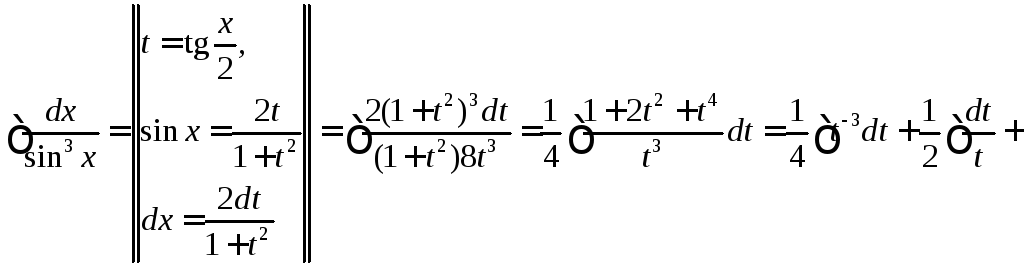
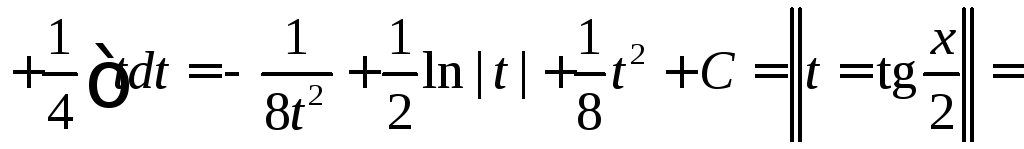
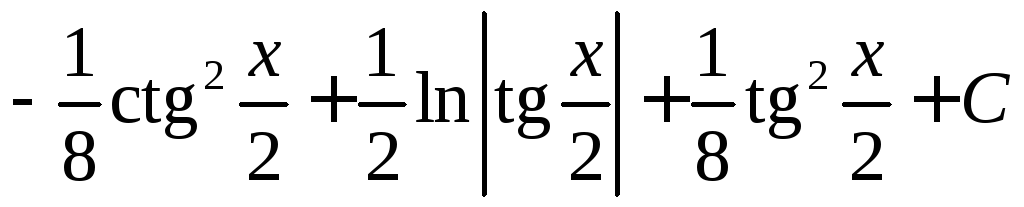 .►
.►
Вычислить
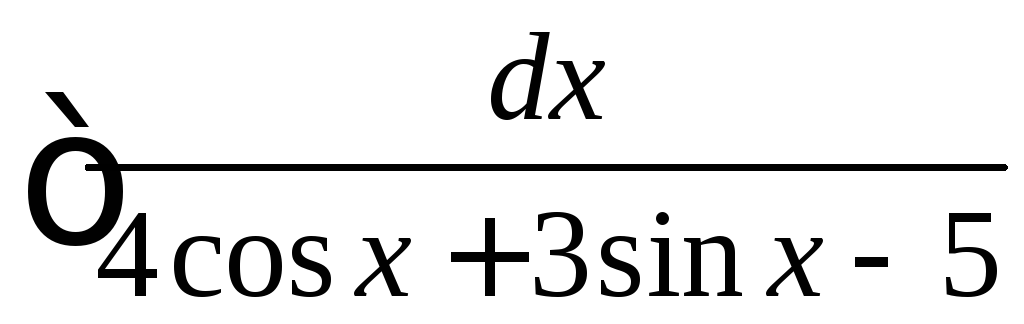 .
.
◄
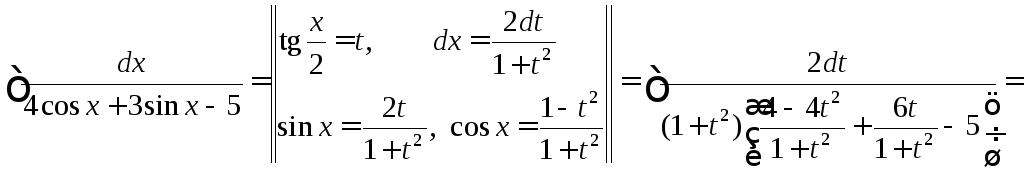
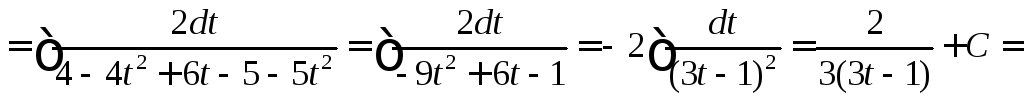
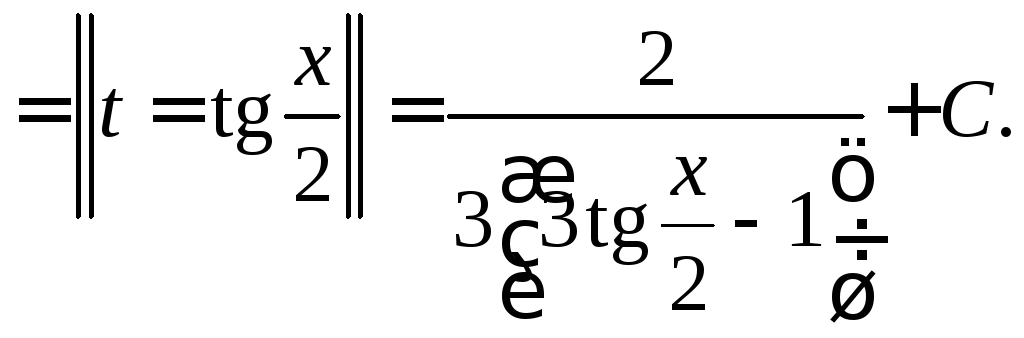 ►
►
Вычислить
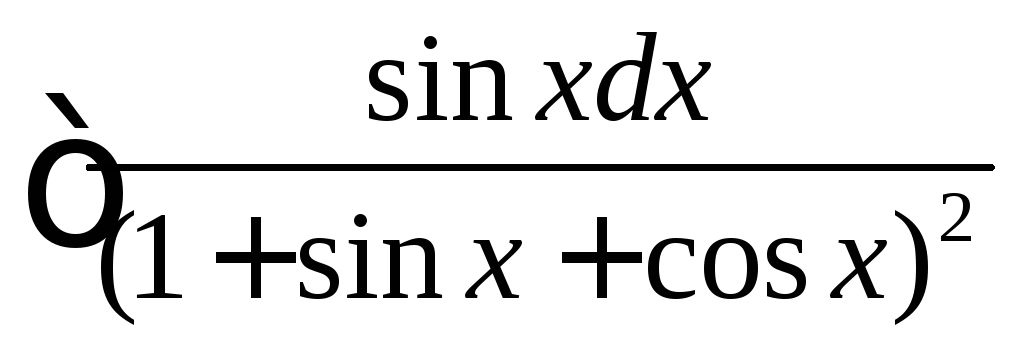 .
.
◄
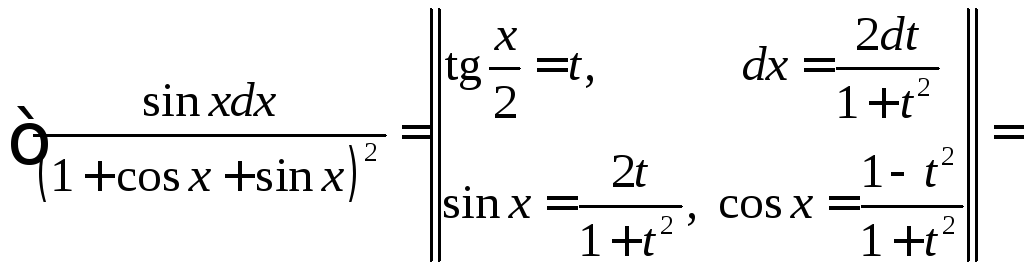
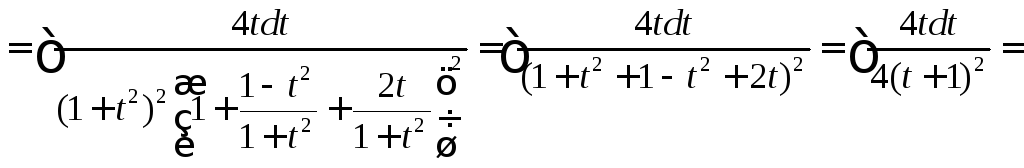
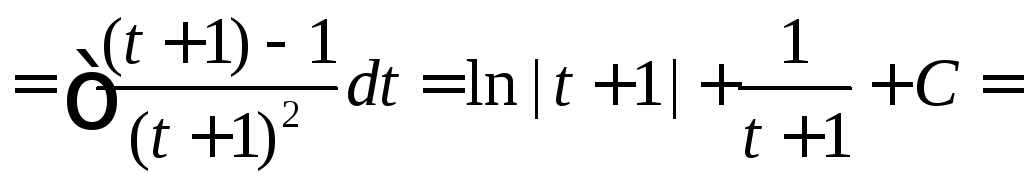
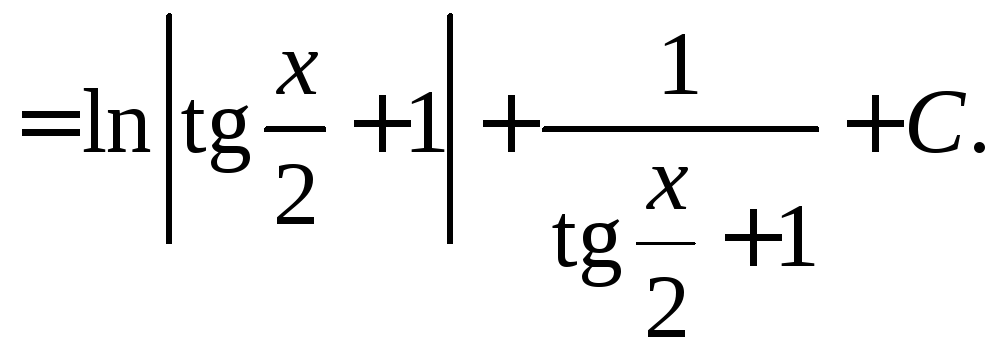 ►
►
Вычислить
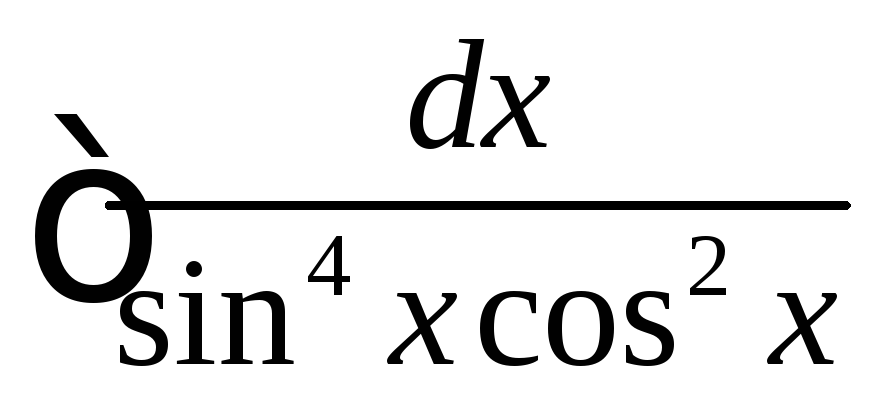 .
.
◄ Так
как
![]() и
и![]() входят в подынтегральную функцию в
чётных степенях, то можно сделать
подстановку
входят в подынтегральную функцию в
чётных степенях, то можно сделать
подстановку
![]() ,
,
![]() .
Используя формулы , получаем
.
Используя формулы , получаем
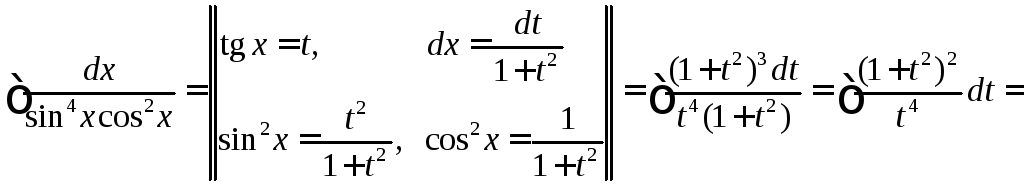
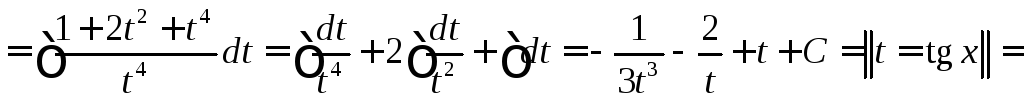
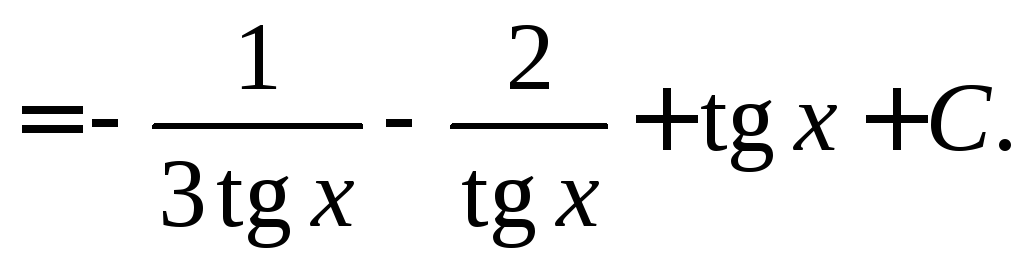 ►
►
Вычислить
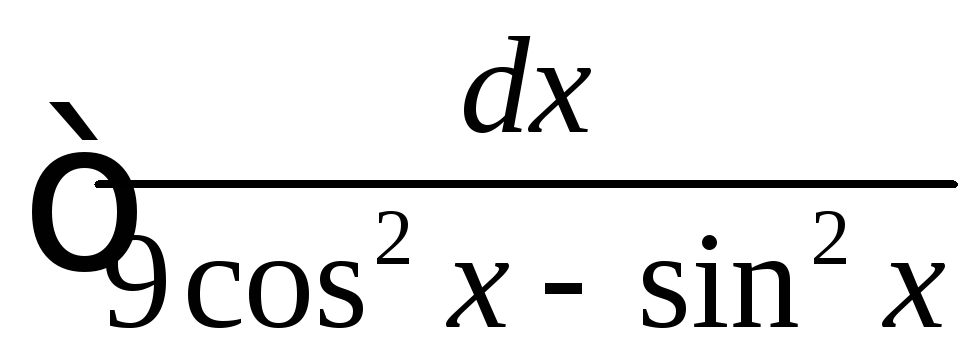 .
.
◄
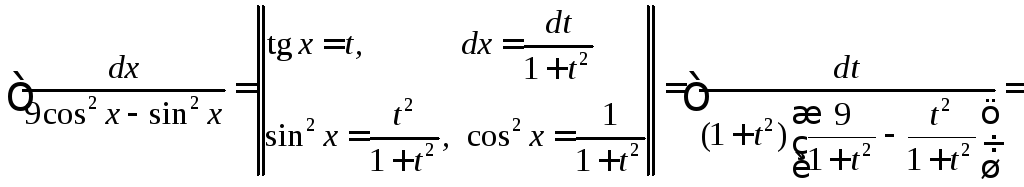
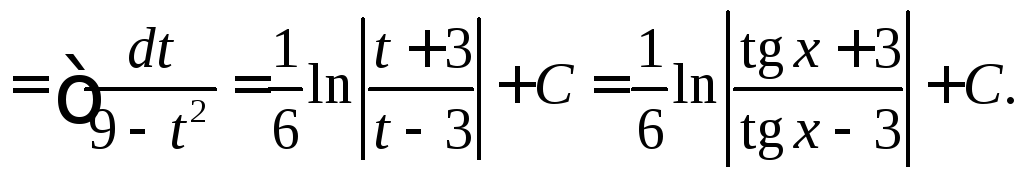 ►
►
Вычислить
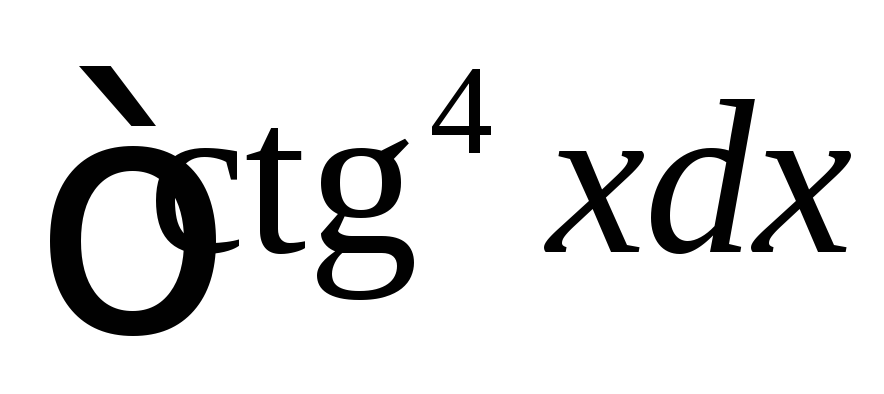 .
.
◄
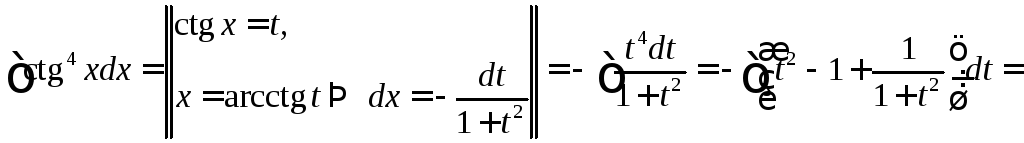
![]() .►
.►
Вычислить
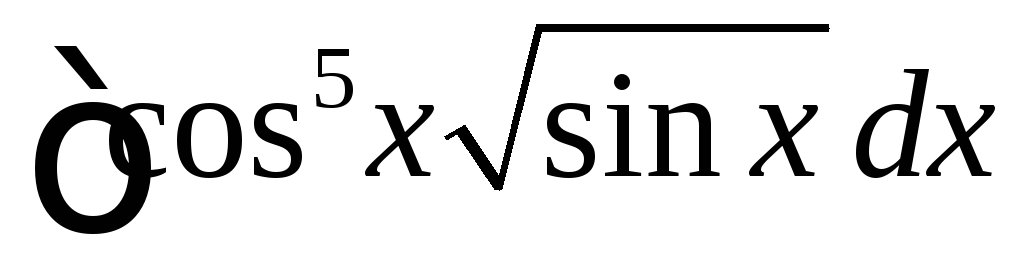 .
.
◄ Используем то обстоятельство, что косинус стоит в нечётной степени.
![]()
![]()
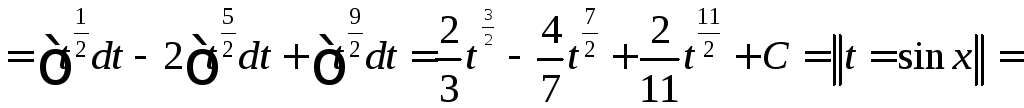
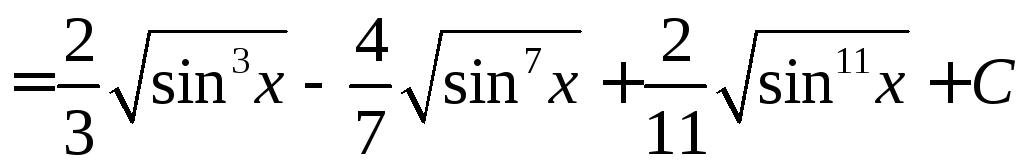 .►
.►
Вычислить
 .
.
◄ Для вычисления этого интеграла от произведения синуса и косинуса в чётных степенях используем формулы понижения степени .
![]()
![]()
![]()
![]() .
►
.
►
Вычислить
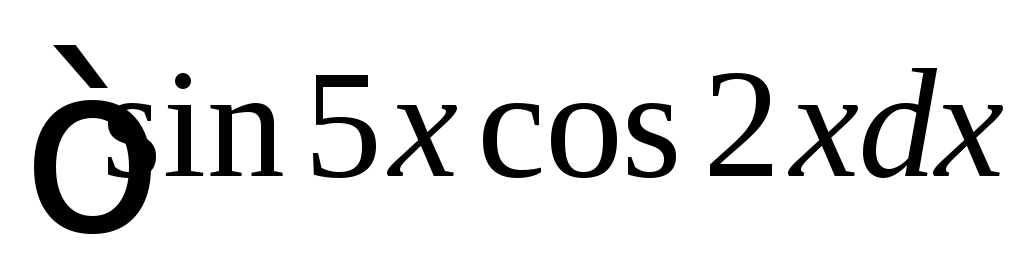 .
.
◄ Используем
формулу :
![]()
![]()
![]()
![]() ►
►
Задачи для самостоятельного решения
Вычислить интегралы.
|
|
| |
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
Интегрирование некоторых иррациональных функций
7.1. Сведения из теории
Далее
будем обозначать
![]() – рациональную функцию аргументов
– рациональную функцию аргументов![]() .
.
7.1.1.
Интегралы вида
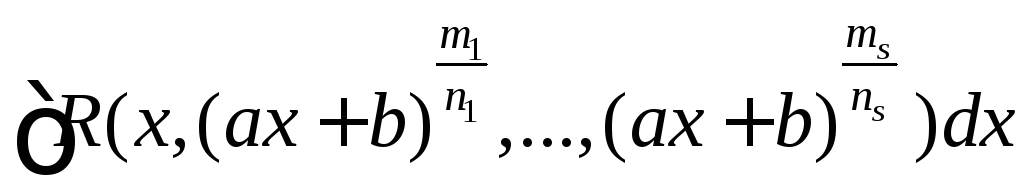 ,
,
где
![]() – целые числа, с помощью подстановки
– целые числа, с помощью подстановки![]() где n
– общий
знаменатель дробей
где n
– общий
знаменатель дробей
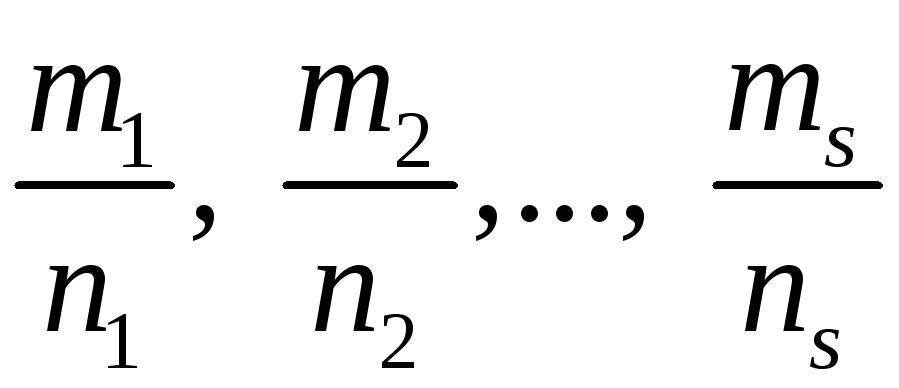 сводятся к интегралам от рациональных
функций переменнойt.
сводятся к интегралам от рациональных
функций переменнойt.
7.1.2. Интегралы вида
![]() ;
;
![]() ;
;
![]()
с помощью тригонометрических подстановок, соответственно,
![]() в
,
в
,
![]() в и
в и
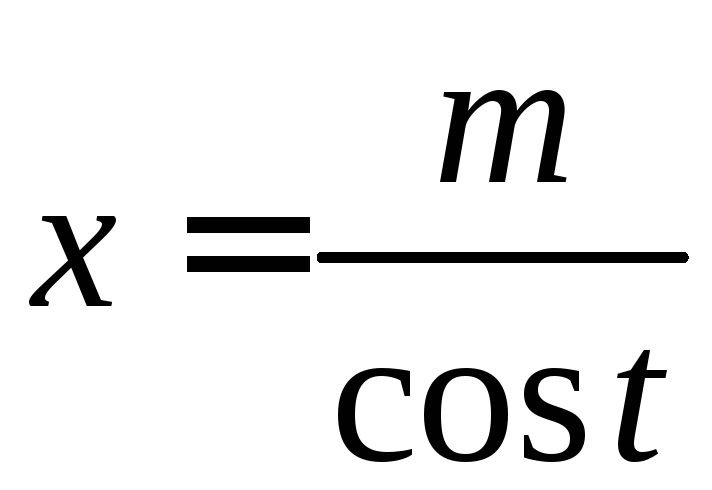 в
в
приводятся
к тригонометрическим интегралам вида
![]() ,
рассмотренным в п.6.
,
рассмотренным в п.6.
7.1.3.
Интегралы вида
![]()
Выделив полный квадрат в квадратном трёхчлене
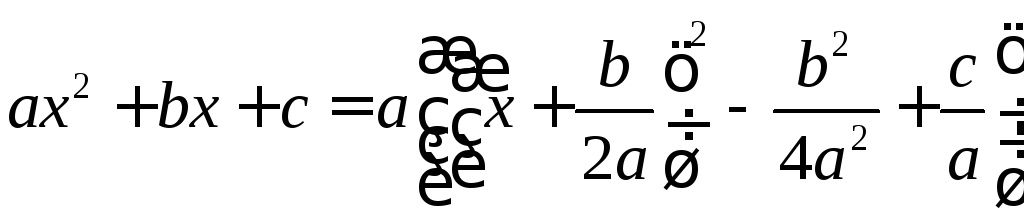
и
сделав замену переменных
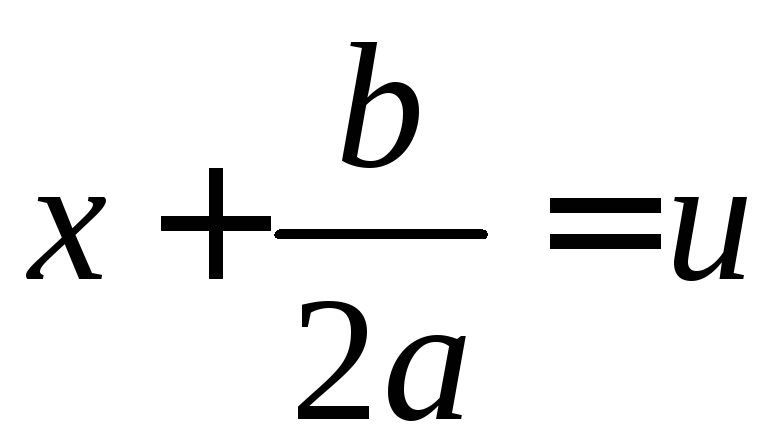 ,
получим интеграл одного из видов ,
или .
,
получим интеграл одного из видов ,
или .
Примеры решения задач
Вычислить
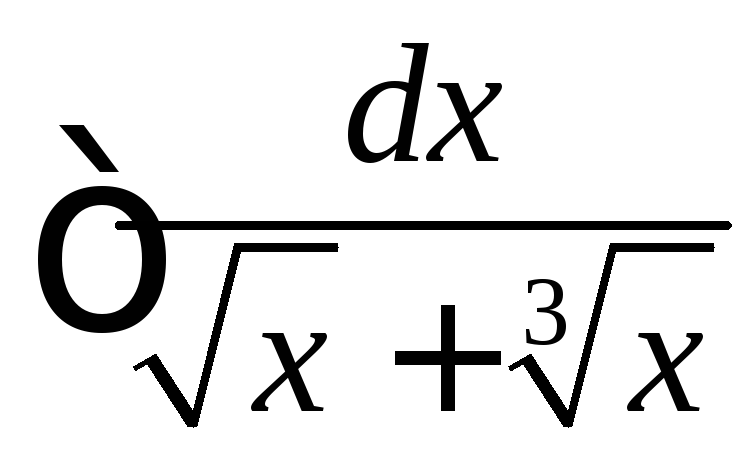 .
.
◄
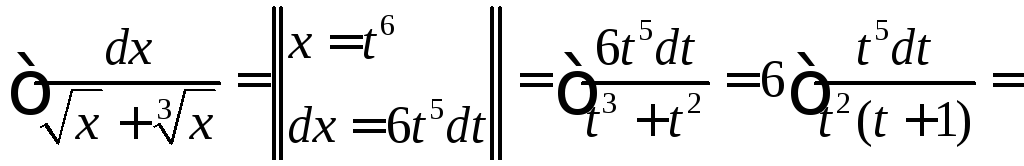
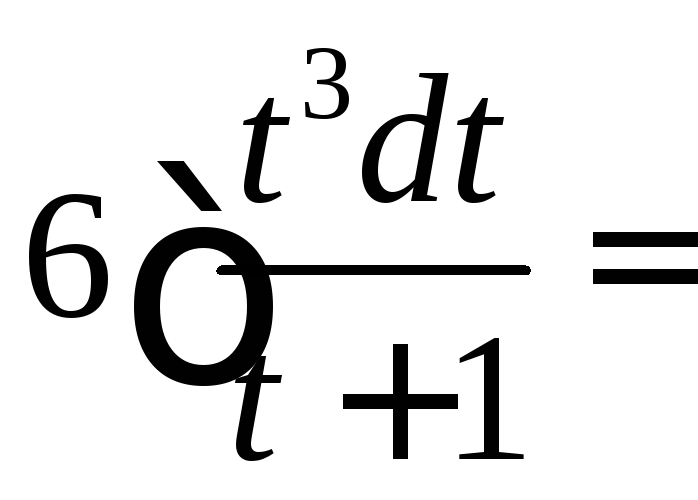
![]()
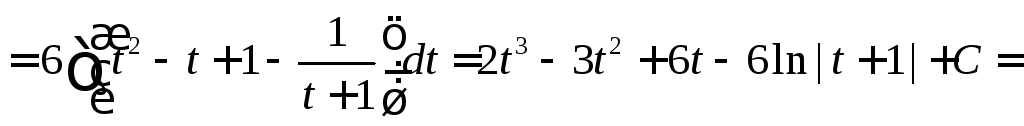
![]()
![]() .
►
.
►
Вычислить

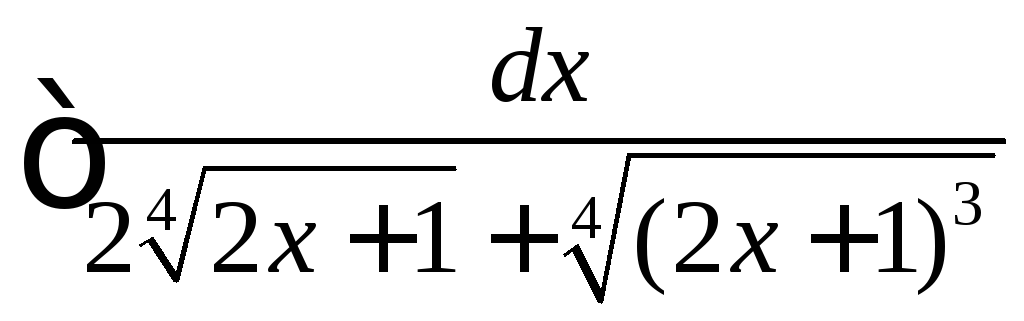 .
.
◄
 =
=
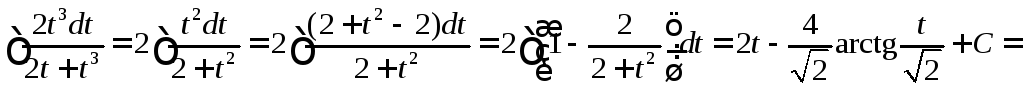
![]()
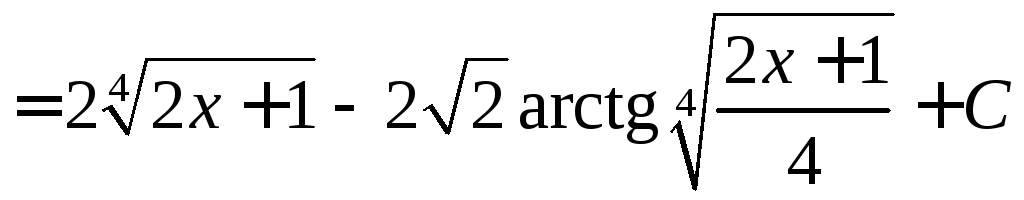 .
►
.
►
Вычислить
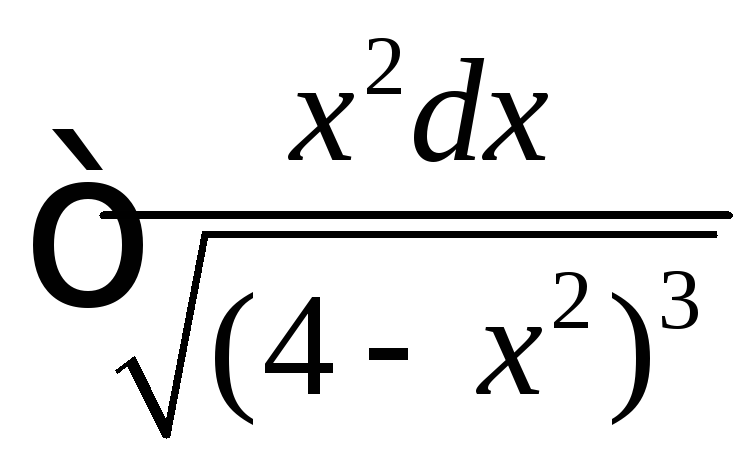 .
.
◄ Рассматриваемый
интеграл имеет вид . Поэтому делаем
тригонометрическую подстановку
![]() ,
,![]() .
.
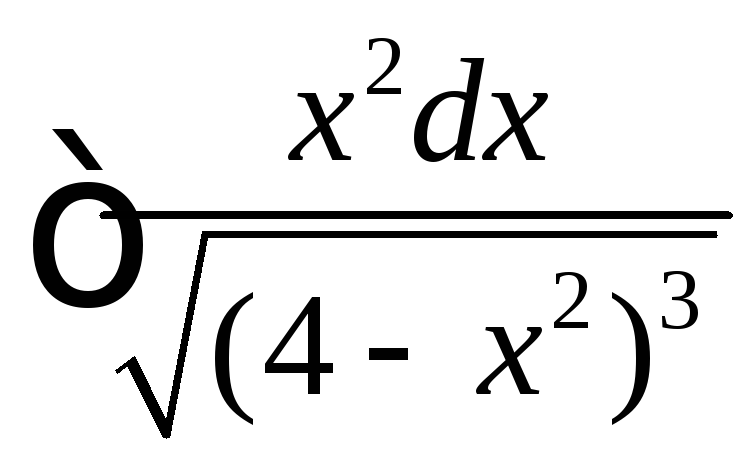 =
=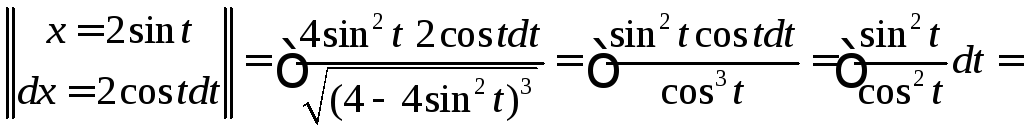
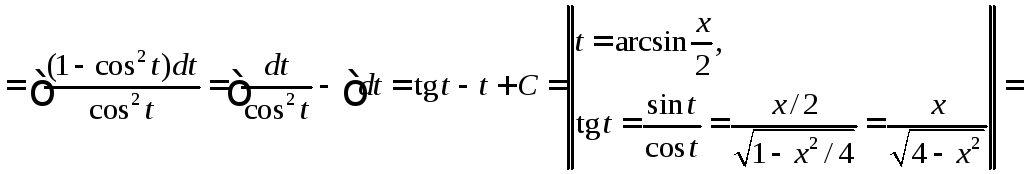
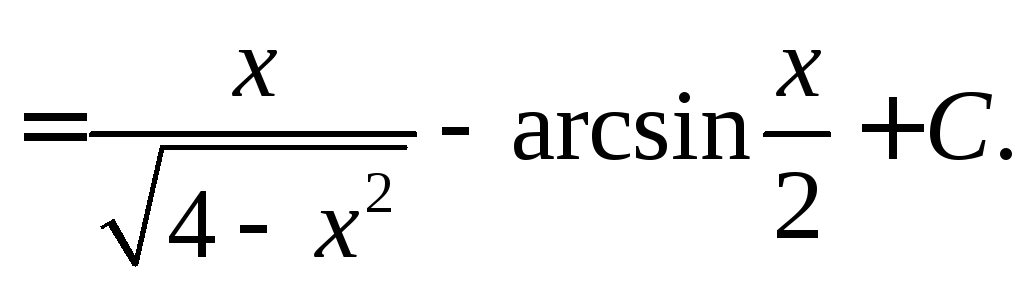 ►
►
Вычислить
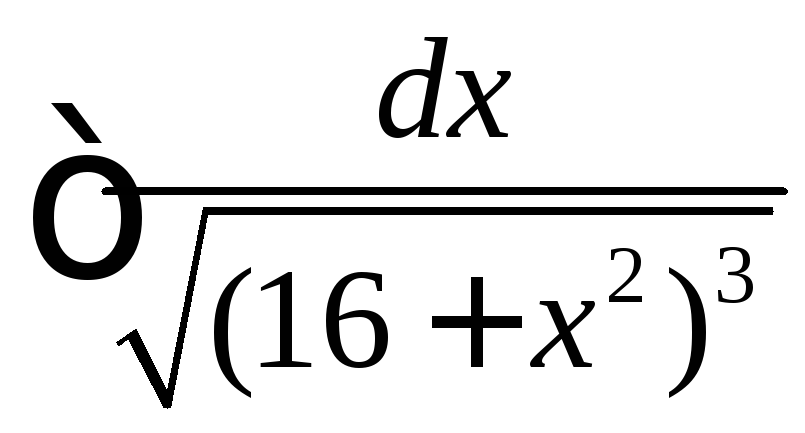 .
.
◄ Рассматриваемый
интеграл имеет вид . Поэтому делаем
тригонометрическую подстановку
![]() ,
,![]() .
.
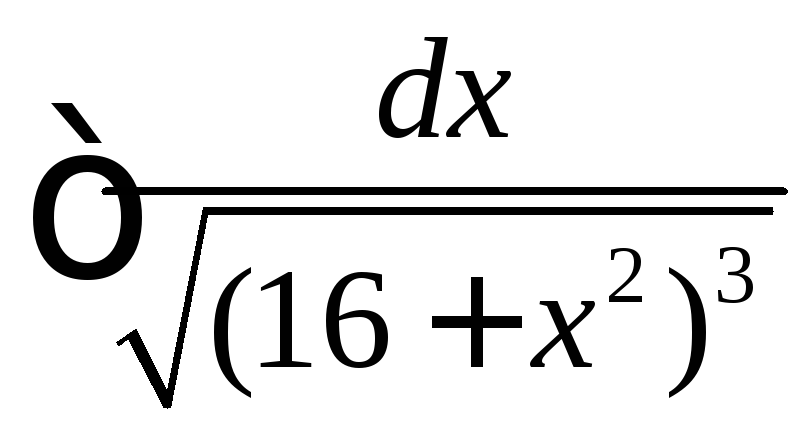
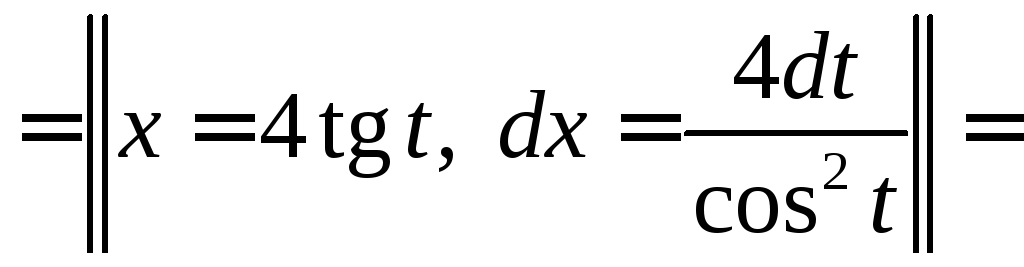
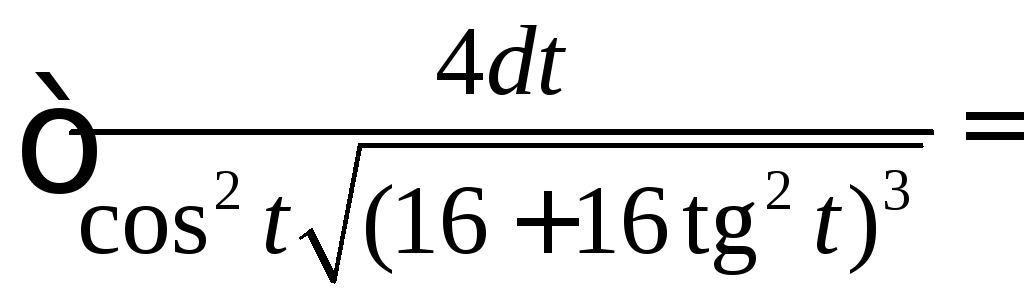 =
=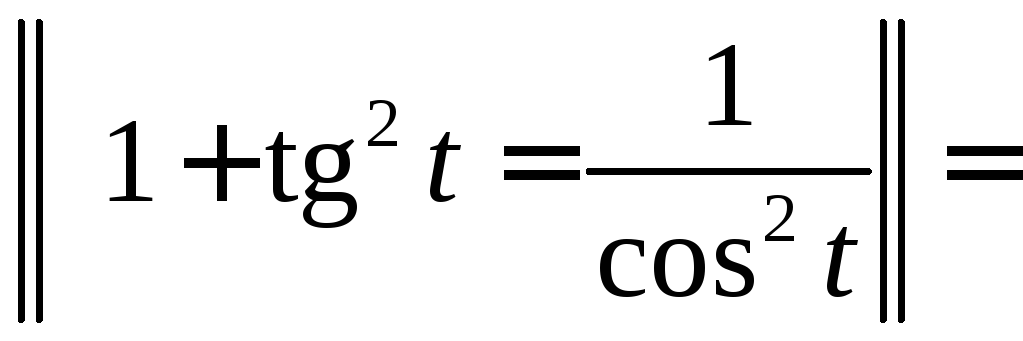
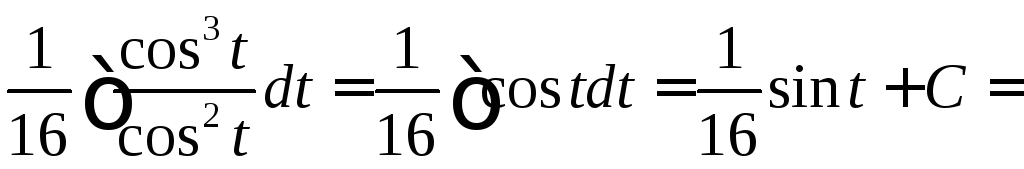
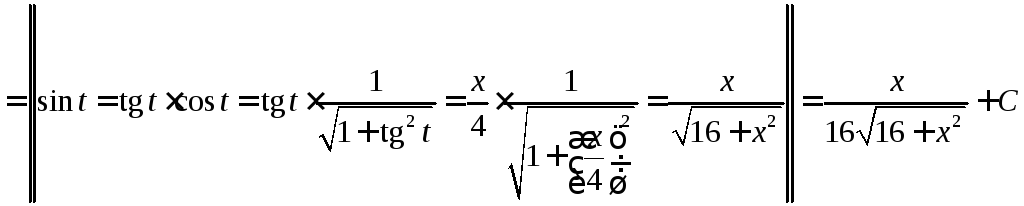 .
►
.
►
Вычислить
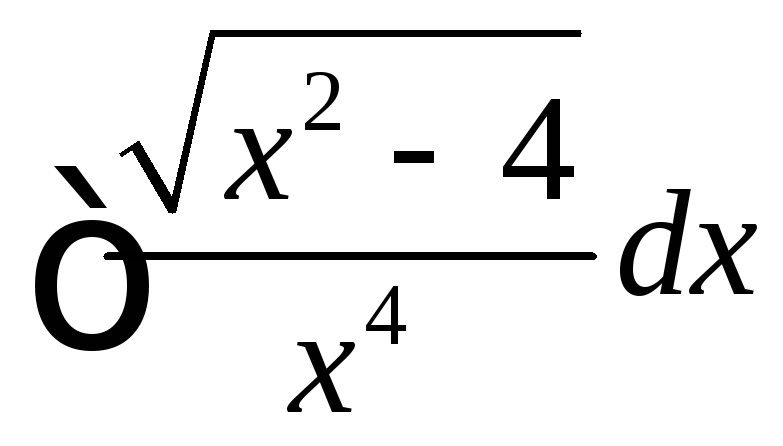 ,
,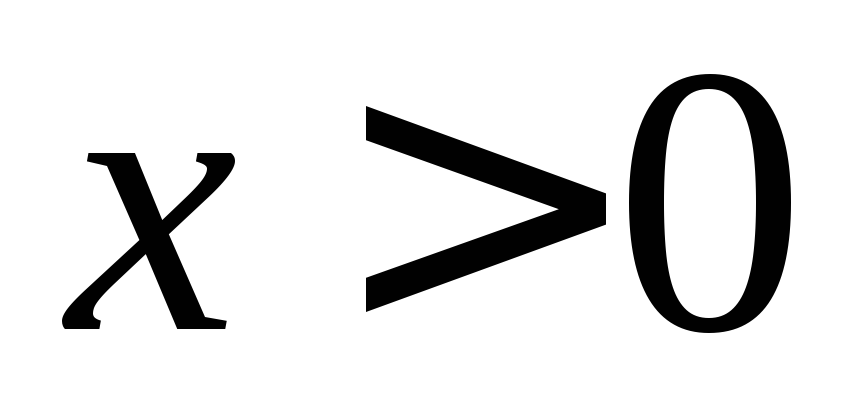 .
.
◄ Рассматриваемый
интеграл имеет вид . Поэтому делаем
тригонометрическую подстановку
![]() (
(![]() .
.
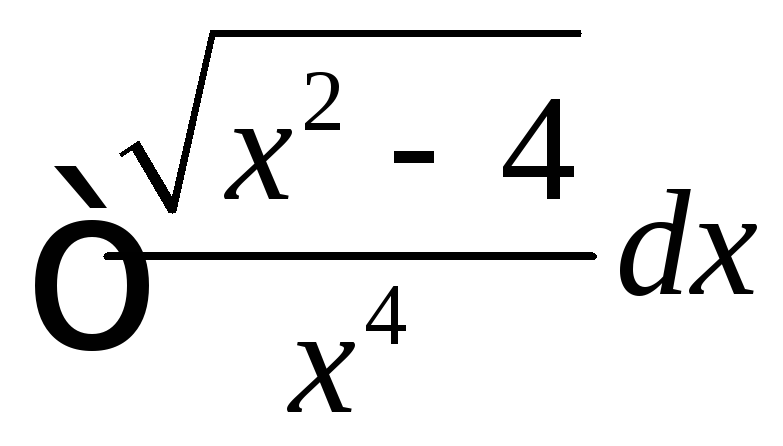
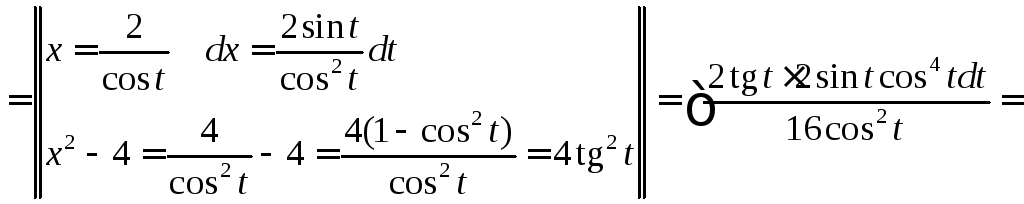
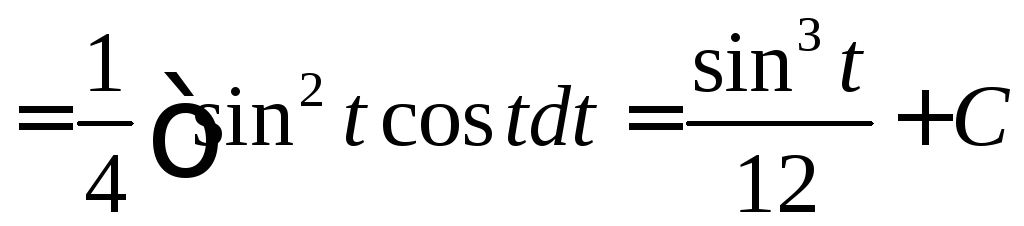 .
Произведем обратную замену:
.
Произведем обратную замену:

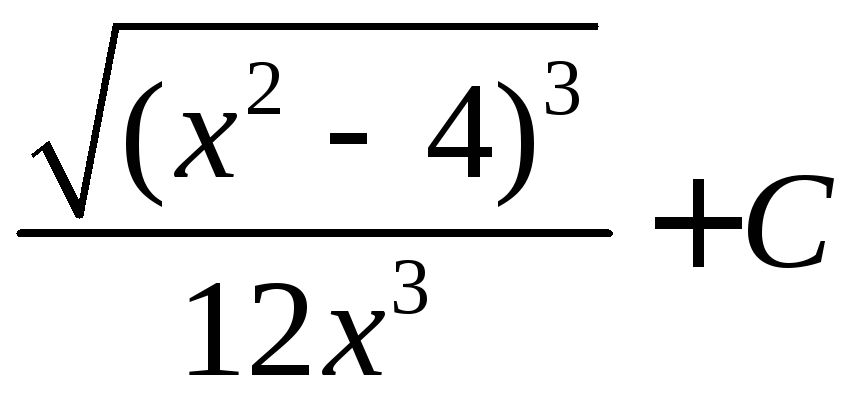 .
►
.
►
Вычислить
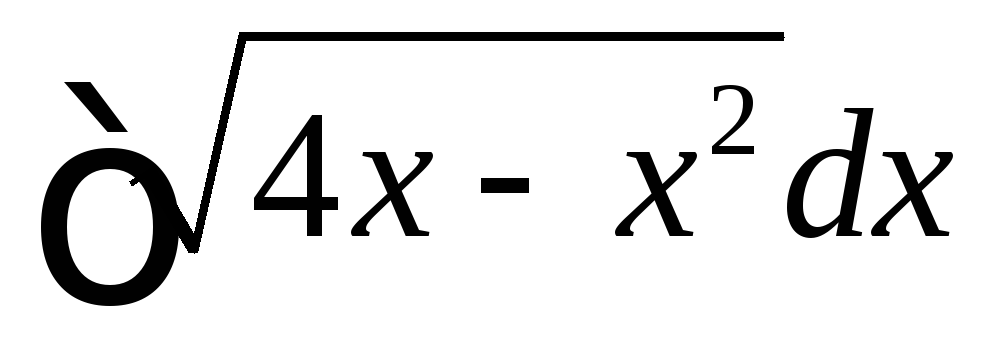 .
.
◄
![]()
![]()
![]()
![]()
![]()
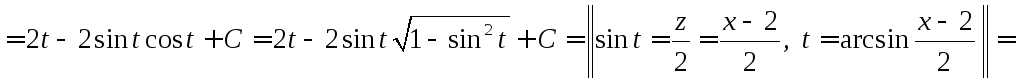
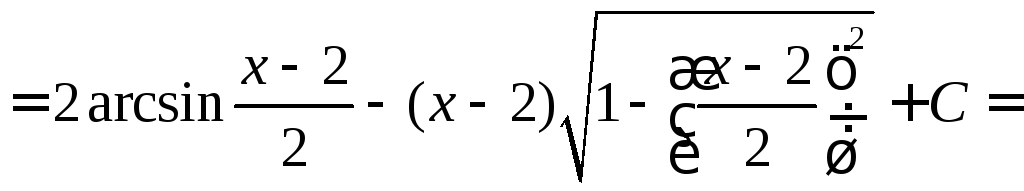
![]()
![]() .►
.►
Задачи для самостоятельного решения
Вычислить интегралы от иррациональных функций.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Понятие определенного интеграла.
Приближенное вычисление определенного интеграла
Основные понятия и формулы (и аналогично в дальнейшем ?)
Пусть
функция
![]() определена на отрезке
определена на отрезке![]() .
Разобьем этот отрезок точками
.
Разобьем этот отрезок точками![]() на частичные отрезки
на частичные отрезки![]() ,
,![]() ,
длины
,
длины![]() .
Наибольшую из этих длин
.
Наибольшую из этих длин![]() назовеммелкостью
разбиения.
В каждом из частичных отрезков
назовеммелкостью
разбиения.
В каждом из частичных отрезков
![]() выберем точку
выберем точку![]() (рис. 1). Составим интегральную сумму
(рис. 1). Составим интегральную сумму
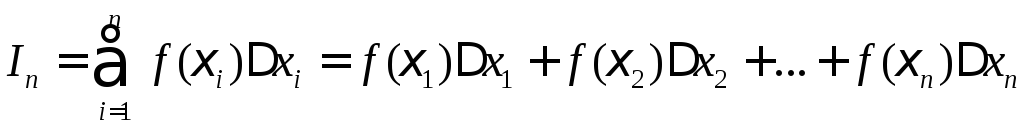 .
.
Определенным
интегралом от функции
![]() по отрезку
по отрезку
![]() (в пределах от
(в пределах от![]() до
до![]() )
называется число (оно обозначается
)
называется число (оно обозначается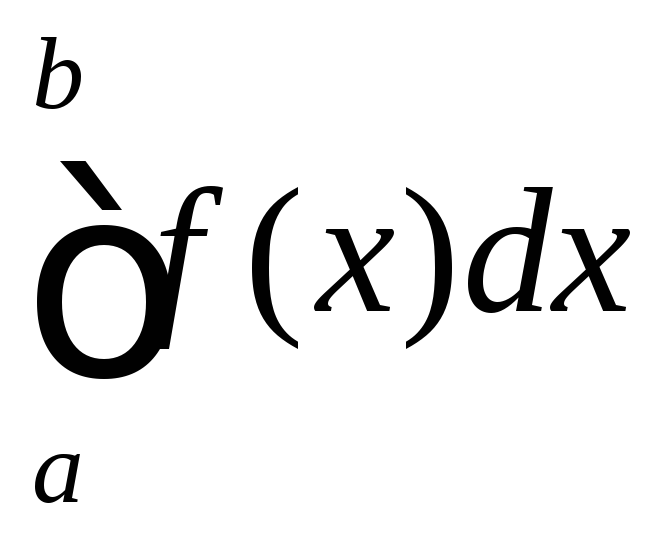 ),
равное пределу интегральных сумм при
неограниченном измельчении разбиения:
),
равное пределу интегральных сумм при
неограниченном измельчении разбиения:
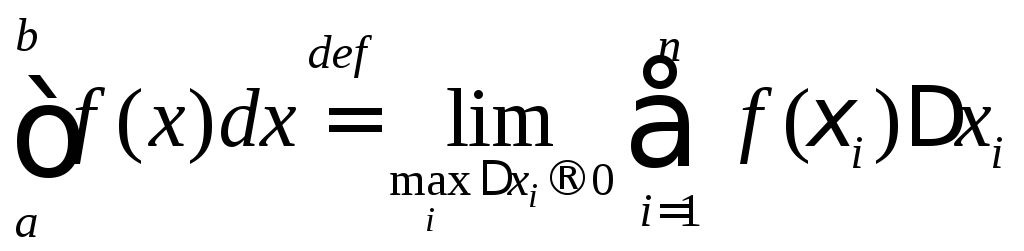 .
.
Точно
это означает следующее: для любого
![]() найдется такое
найдется такое![]() ,
что для любого разбиения с мелкостью
,
что для любого разбиения с мелкостью![]() при любом выборе точек
при любом выборе точек![]() выполняется неравенство
выполняется неравенство
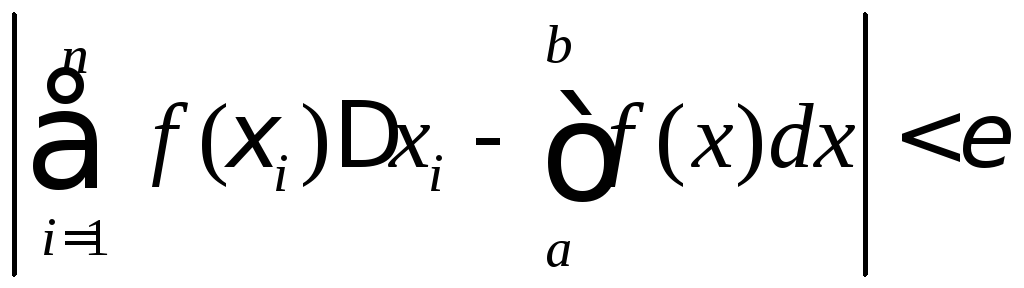 .
.
Для
функций, непрерывных или кусочно-непрерывных
на отрезке
![]() ,
определенный интеграл по этому отрезку
существует –функция
интегрируема по отрезку
,
определенный интеграл по этому отрезку
существует –функция
интегрируема по отрезку
![]() .
.
Полагают также, что
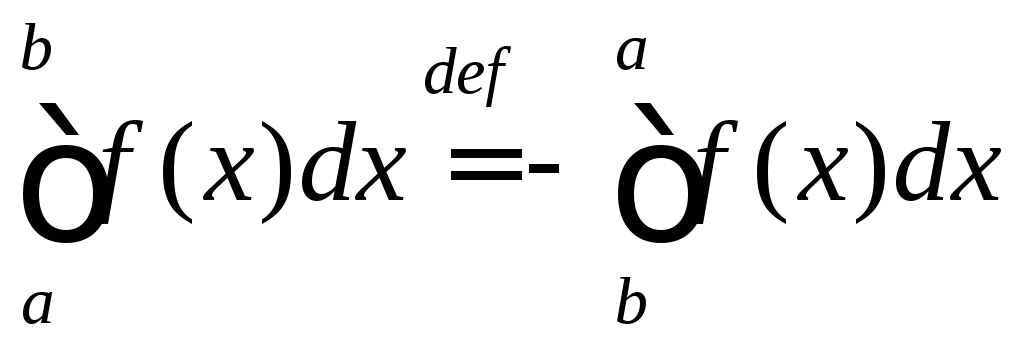 при
при
![]() ;
и
;
и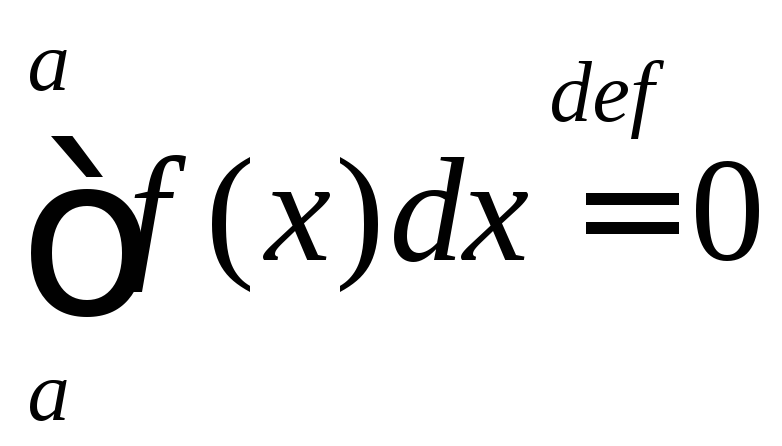 .
.
Из
определения интеграла следует и
простейший метод его приближенного
вычисления – метод
прямоугольников.
Разбиваем отрезок
![]() на достаточно большое число
на достаточно большое число![]() равных отрезков длины
равных отрезков длины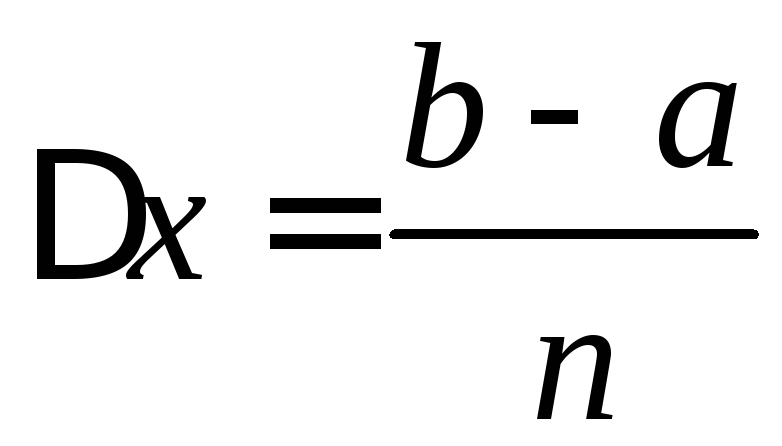 ,
за
,
за![]() берем середину
берем середину![]() -го
отрезка1
-го
отрезка1
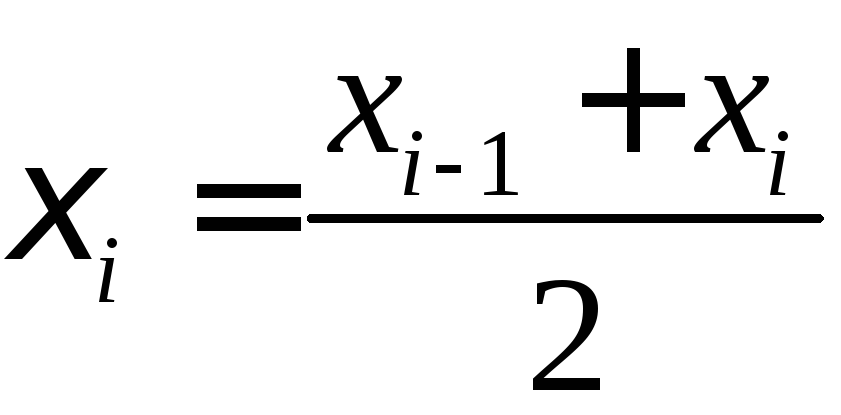 .
В качестве приближенного значения
интеграла принимаем интегральную сумму:
.
В качестве приближенного значения
интеграла принимаем интегральную сумму:
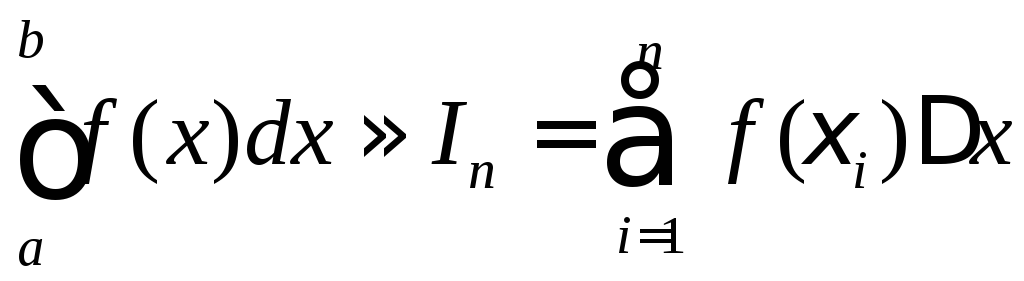 .
.
Каждое
слагаемое в интегральной сумме является
площадью прямоугольника с высотой
![]() и основанием
и основанием![]() (рис.1),
откуда и происходит название метода.
(рис.1),
откуда и происходит название метода.
Оценка
точности метода прямоугольников:
если при некотором значении
![]()
![]() ,
то
,
то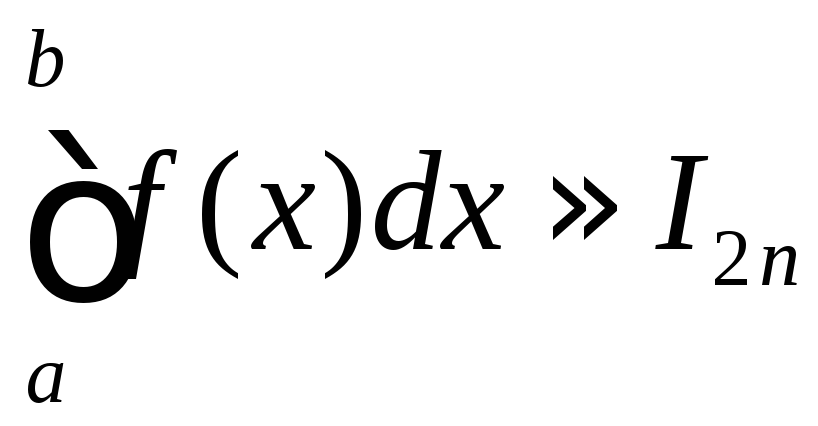 с точностью до
с точностью до![]() .
.
Примеры решения задач
Вычислить
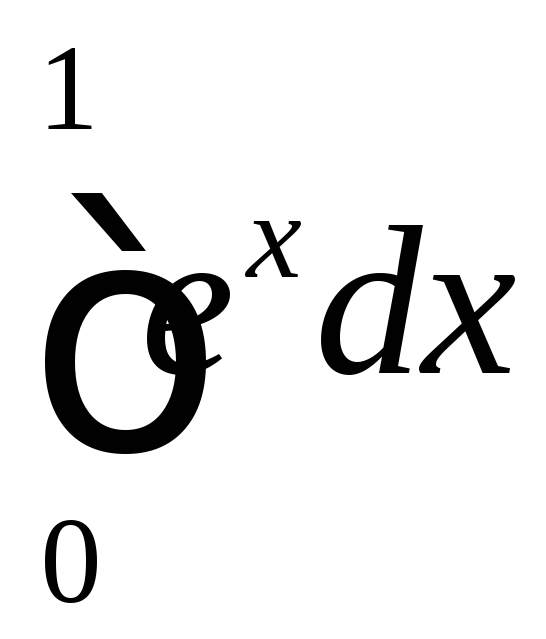 по определению, как предел интегральных
сумм.
по определению, как предел интегральных
сумм.
◄ Отрезок
интегрирования
![]() разобьем точками
разобьем точками![]() ,
, ,
,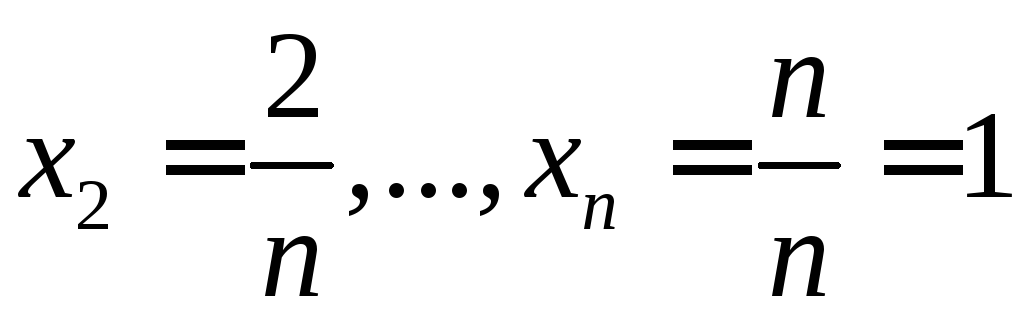 на частичные отрезки
на частичные отрезки![]() ,
,![]() ,
одинаковой длины
,
одинаковой длины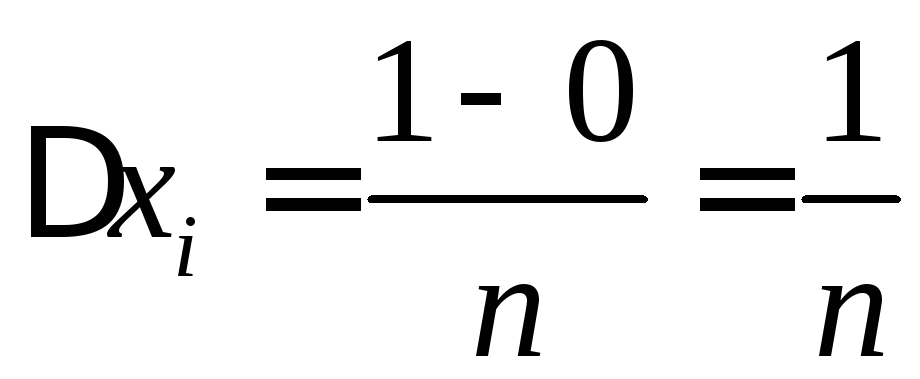 .
Возьмем
.
Возьмем![]() ,
,![]() .
Составим интегральную сумму для функции
.
Составим интегральную сумму для функции![]()
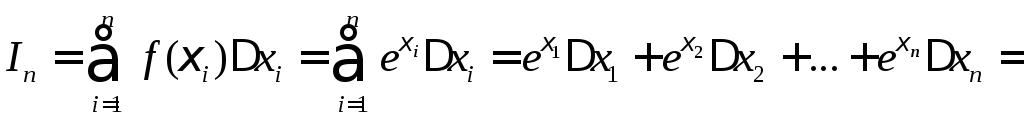
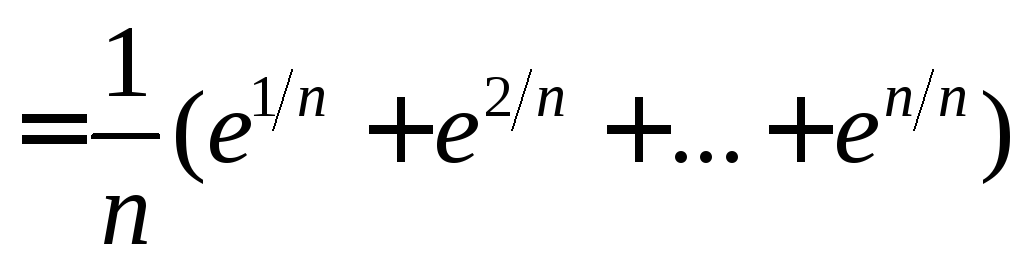 .
.
В
скобках стоит сумма первых
![]() членов геометрической прогрессии со
знаменателем
членов геометрической прогрессии со
знаменателем![]() и первым членом
и первым членом![]() .
Она равна
.
Она равна
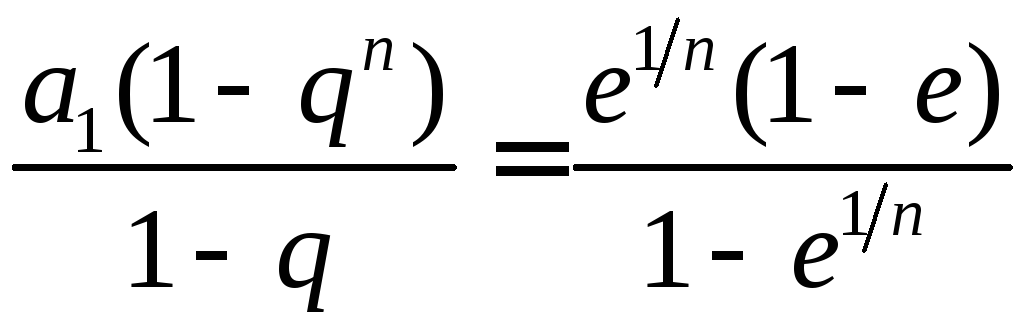 .
.
Поэтому интегральная сумма
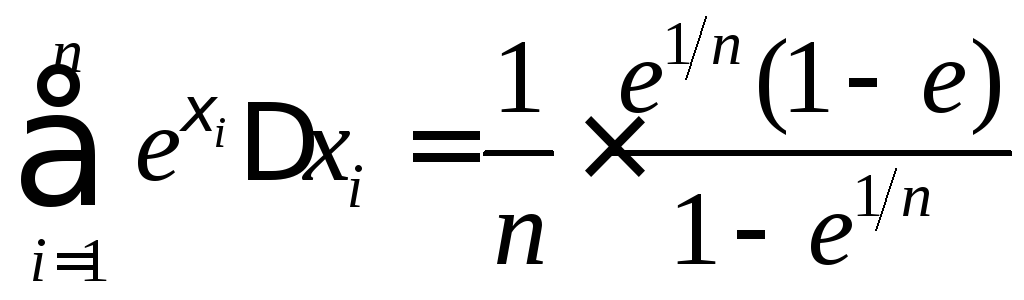 .
.
Вычислим
теперь интеграл как предел интегральных
сумм при
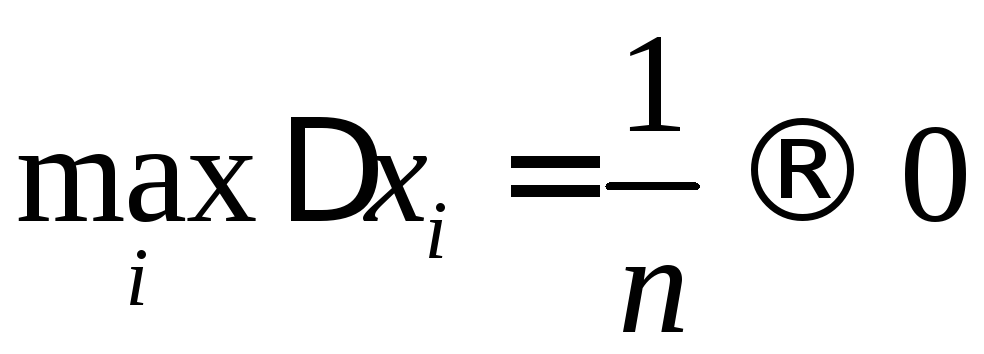 (
(![]() ).
).


![]() .►
.►
Вычислить приближенно
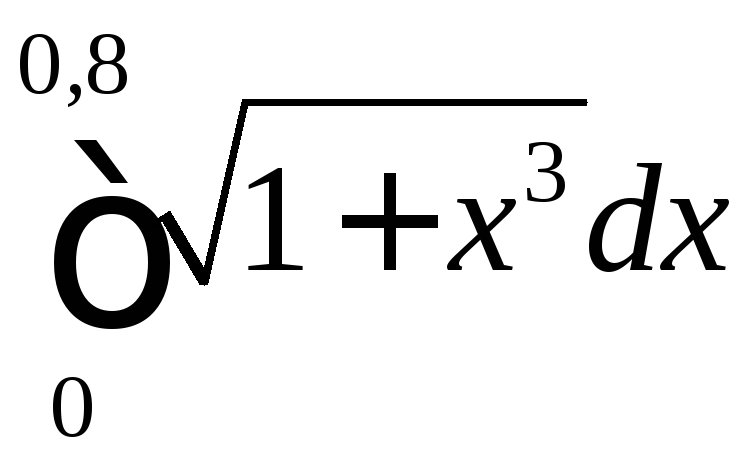 методом прямоугольников (методом
средних) с точностью до
методом прямоугольников (методом
средних) с точностью до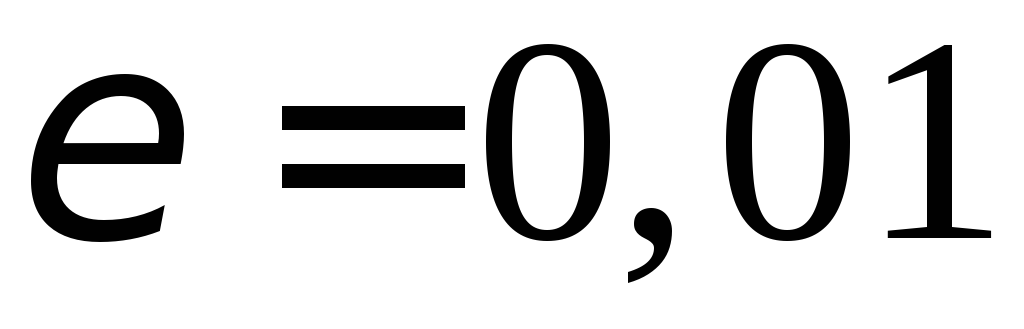 .
.
◄ Разобьем
отрезок
![]() на
на![]() равных отрезков. Их длина
равных отрезков. Их длина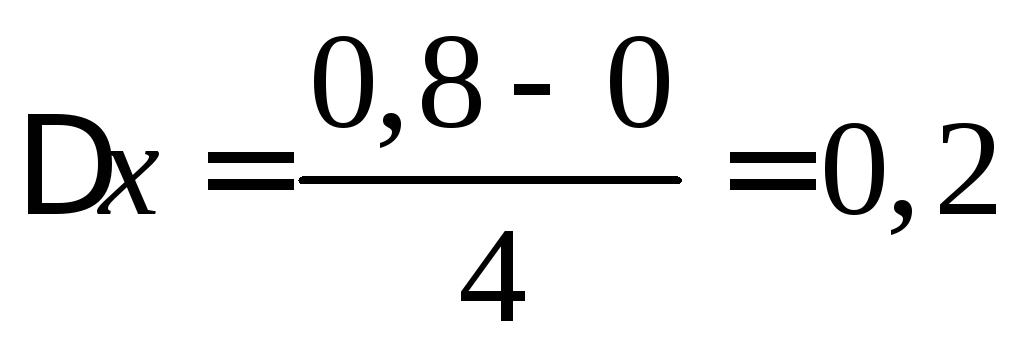 .
Поэтому точки деления
.
Поэтому точки деления![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Составим табл. 1.
.
Составим табл. 1.
Таблица 1
|
|
|
|
|
1 |
0,1 |
1, 0005 |
|
2 |
0,3 |
1,0134 |
|
3 |
0,5 |
1,0607 |
|
4 |
0,7 |
1,1589 |
По формуле прямоугольников
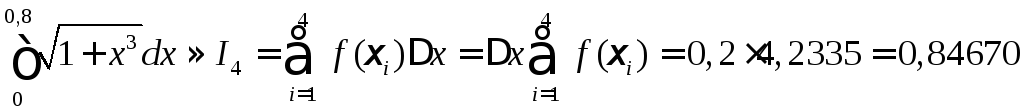 .
.
Разобьем
отрезок
![]() на
на![]() равных отрезков. Их длина
равных отрезков. Их длина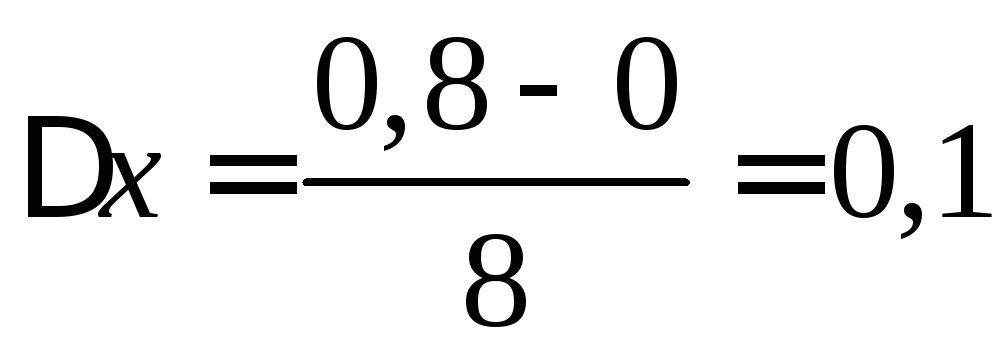 .
Поэтому точки деления
.
Поэтому точки деления![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() .
Составим табл. 2.
.
Составим табл. 2.
Таблица 2
|
|
|
|
|
1 |
0,05 |
1,0001 |
|
2 |
0,15 |
1,0017 |
|
3 |
0,25 |
1,0078 |
|
4 |
0,35 |
1,0212 |
|
5 |
0,45 |
1,0446 |
|
6 |
0,55 |
1,0800 |
|
7 |
0,65 |
1,1290 |
|
8 |
0,75 |
1,1924 |
По формуле прямоугольников
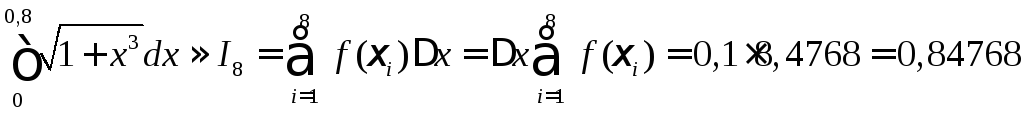 .
.
Поскольку
![]() ,
то с точностью до
,
то с точностью до![]()
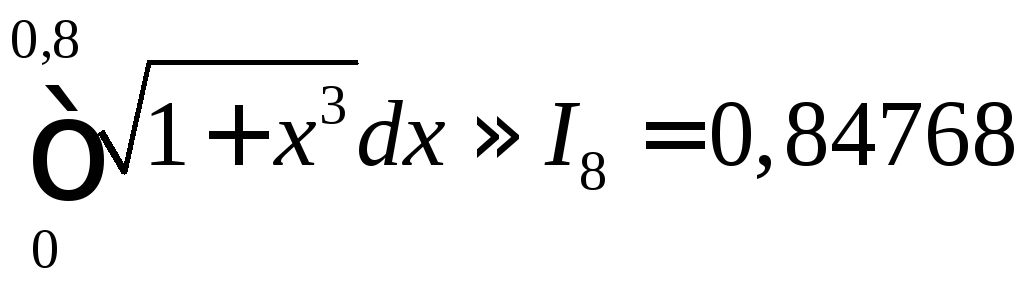 .
Округляя до сотых, получаем окончательно
.
Округляя до сотых, получаем окончательно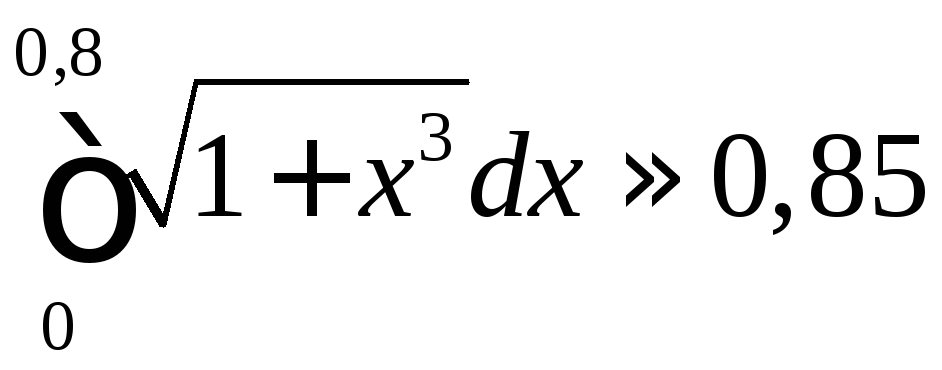 .
.
Замечание.
Для другой подынтегральной функции или
при другом
![]() могло бы оказаться, что
могло бы оказаться, что![]() .
Тогда для достижения заданной точности
.
Тогда для достижения заданной точности![]() следует продолжить вычисление интегральных
сумм
следует продолжить вычисление интегральных
сумм![]() ,
,![]() ,
,![]() ,
… до тех пор, пока абсолютная величина
разности двух соседних членов этой
последовательности не станет
,
… до тех пор, пока абсолютная величина
разности двух соседних членов этой
последовательности не станет![]() .
►
.
►
Задачи для самостоятельного решения
Вычислить интеграл
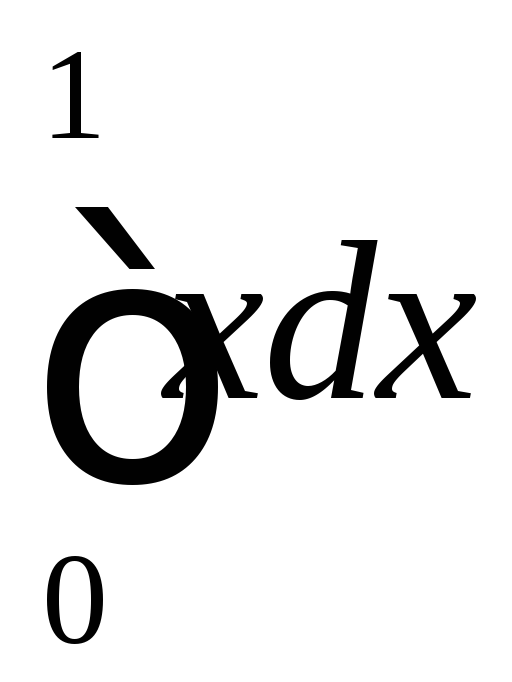
а) по определению как предел интегральных сумм,
б) приближенно методом прямоугольников с точностью 0,01 .
Указание. В пункте а) использовать равенство
 .
.
Вычислить пределы
а)
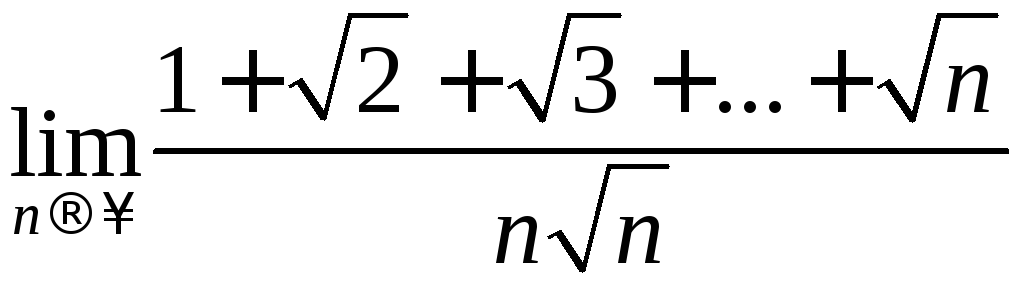 ,
б)
,
б)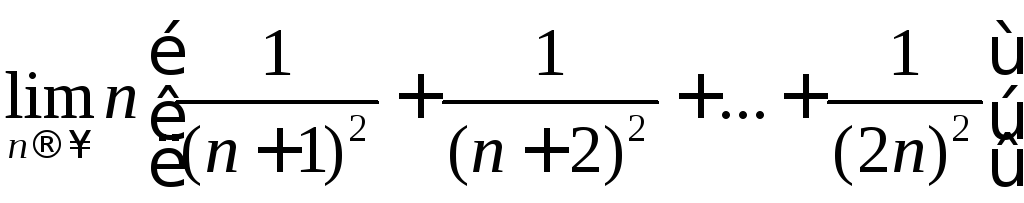 .
.
Указание. Записать эти пределы как пределы интегральных сумм. Соответствующие интегралы вычислить по формуле Ньютона-Лейбница (2.1).

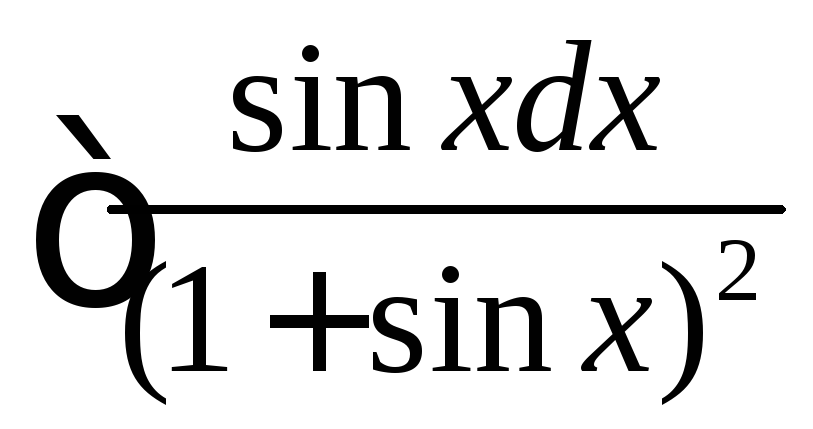 .
.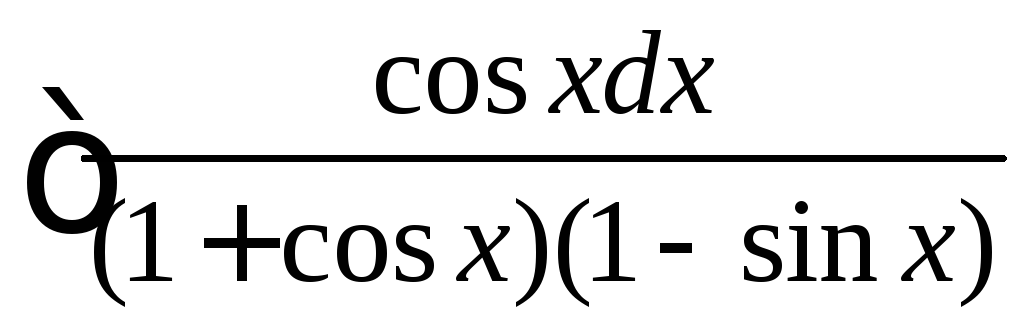 .
.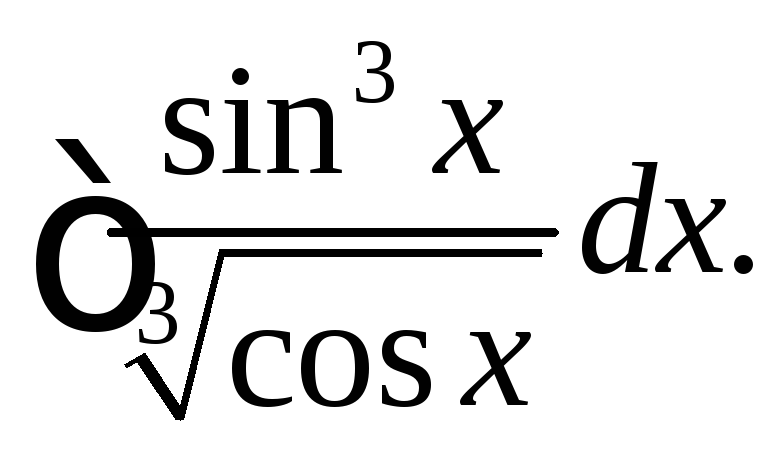
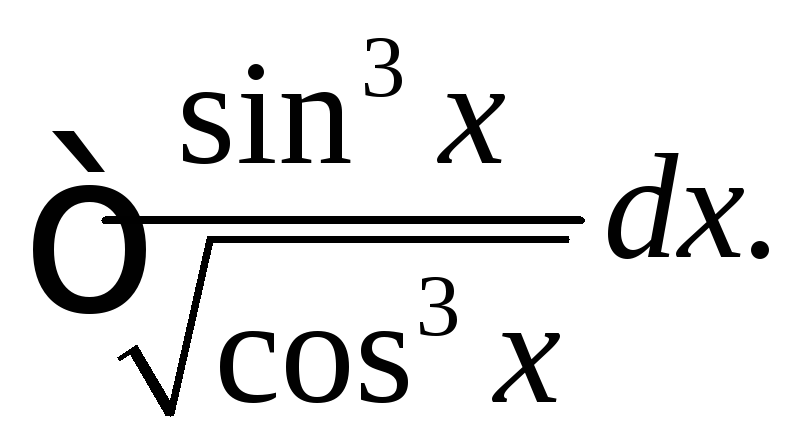
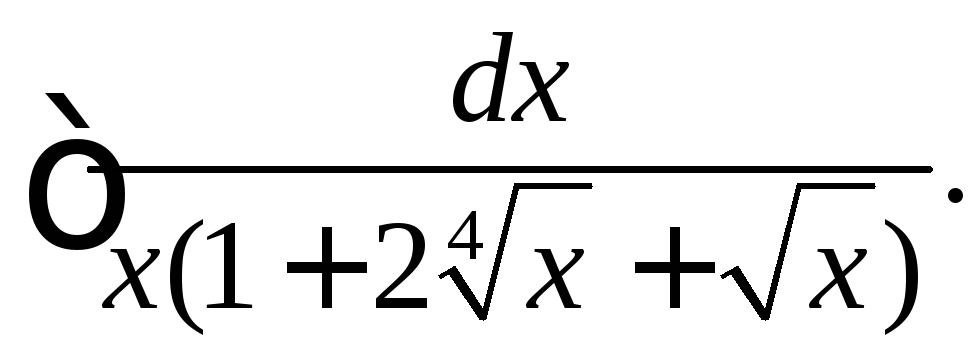
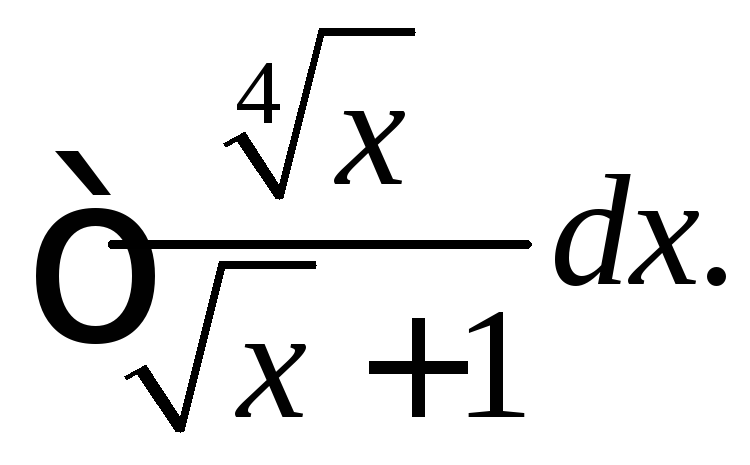
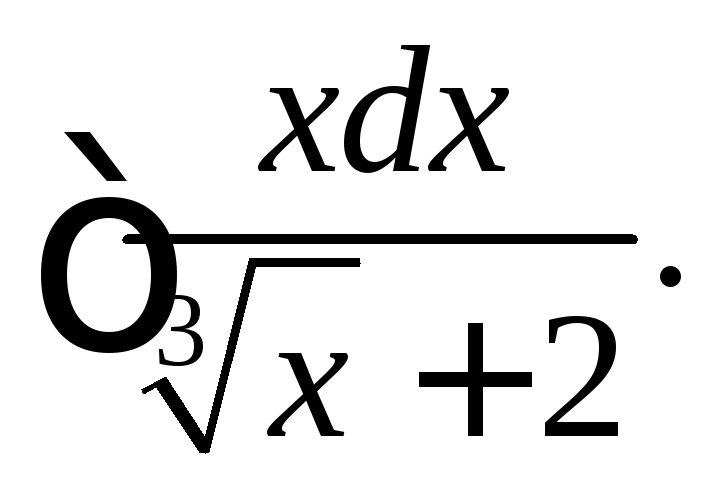
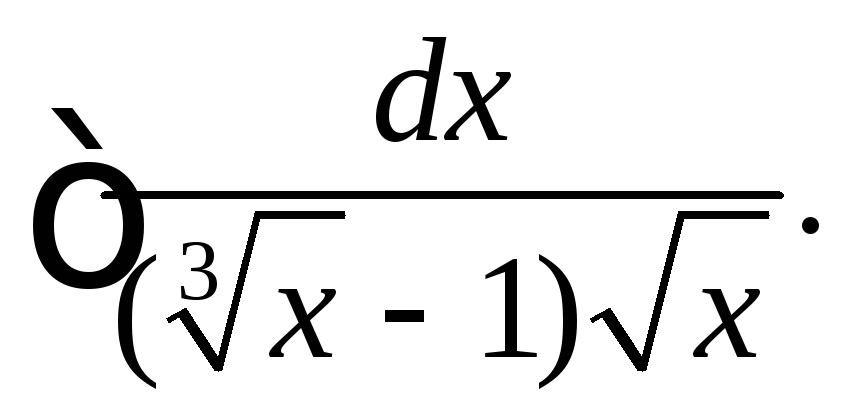
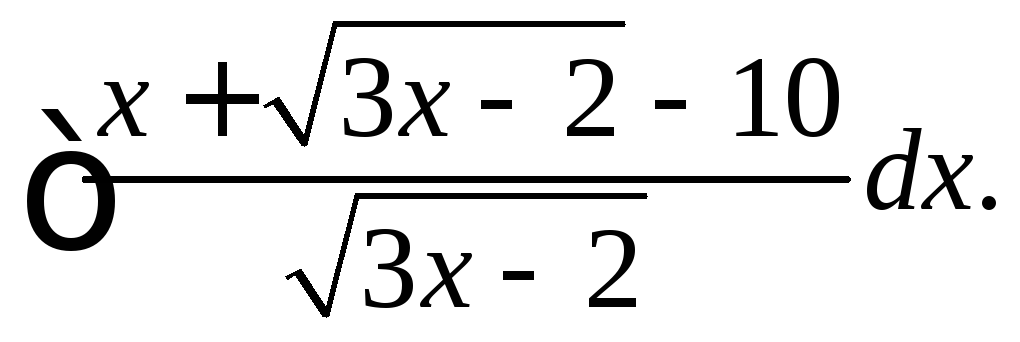
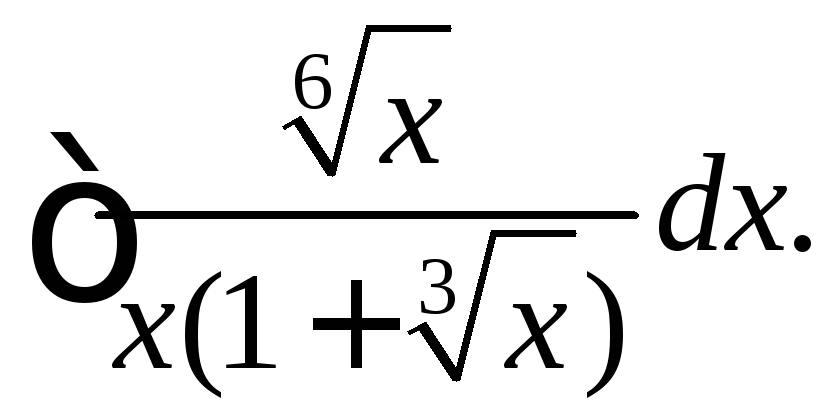
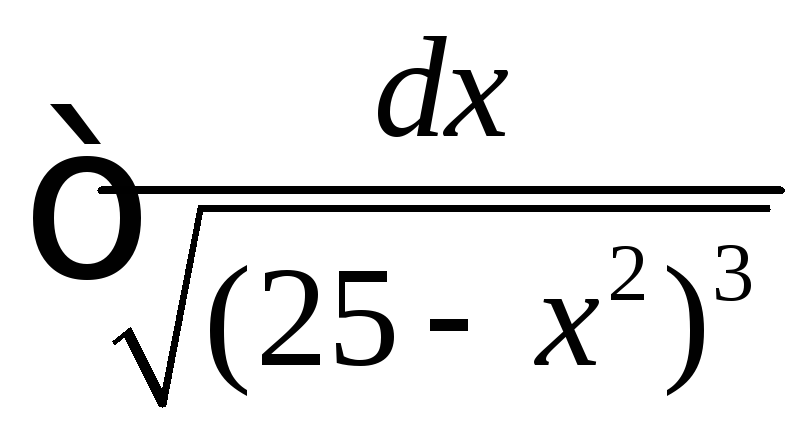 .
.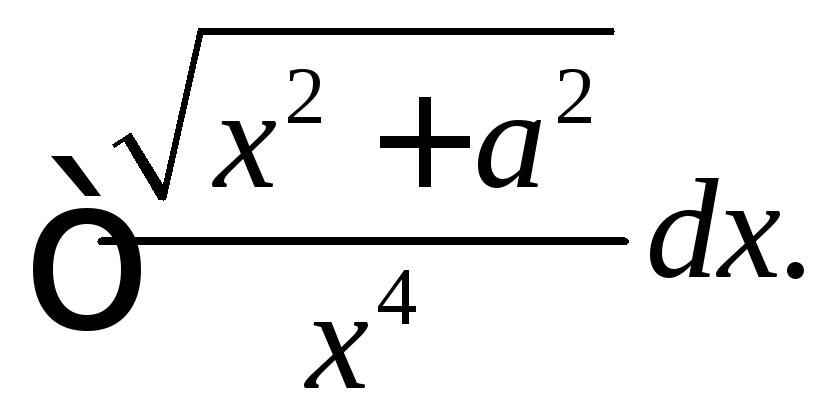
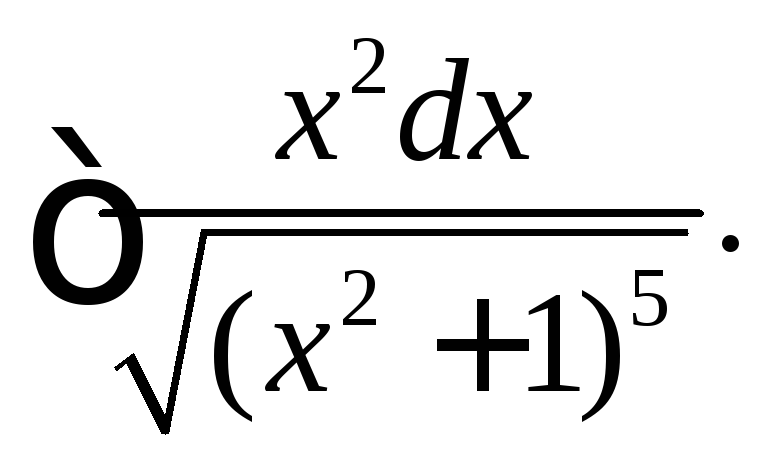
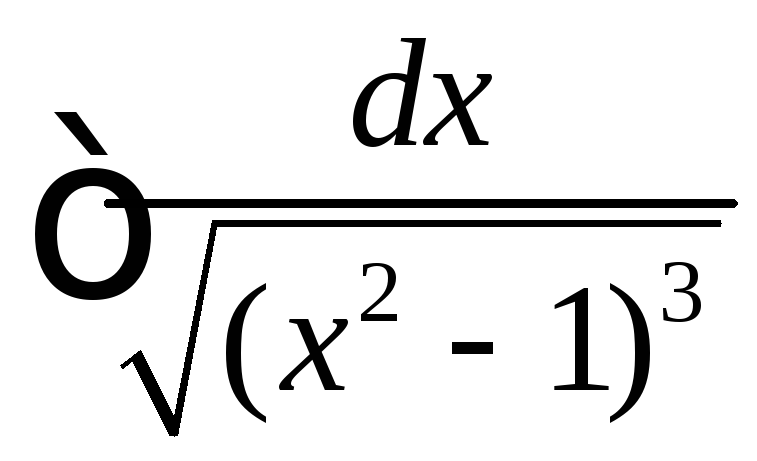 .
.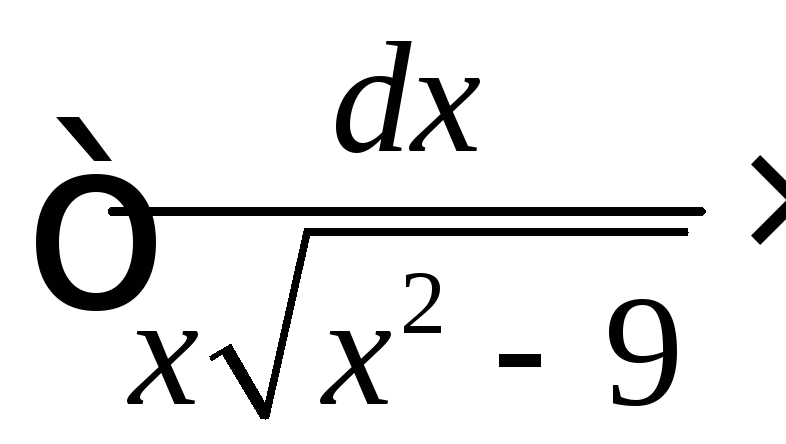
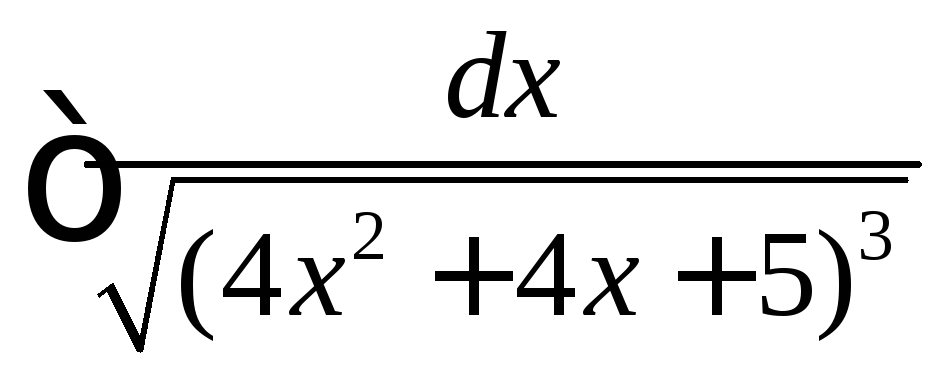 .
.