
- •Докажите, что допустимая область является выпуклым множеством.
- •Дайте характеристику канонической формы задачи лп.
- •Назовите основные шаги симплекс-метода.
- •Основные правила перехода к двойственной задаче.
- •Алгоритм решения задачи
- •Математическая модель задачи
- •Анализ результатов вычислений
- •Список использованных источников
-
Назовите основные шаги симплекс-метода.
На первом этапе находят одно из решений, удовлетворяющее системе ограничений. Системы, в которых переменных больше, чем ограничений N > m, называются неопределенными. Они приводятся к определенным системам (N = m) путем приравнивания к нулю N-m каких-либо переменных. При этом остается система m уравнений с m неизвестными, которая имеет решение, если определитель системы отличен от нуля. В симплекс-методе вводится понятие базисных переменных, или базиса. Базисом называется любой набор из m таких переменных, что определитель, составленный из коэффициентов при этих переменных в m-ограничениях, отличен от нуля. Остальные N-m переменных называются небазисными, или свободными переменными. Если принять, что все небазисные переменные равны нулю, и решать систему ограничений относительно базисных переменных, то получится базисное решение.
В системе из m уравнений с N неизвестными общее число базисных решений при N > m определяется числом сочетаний
Базисное решение, в котором все xi0, i = 1,m, называется допустимым базисным решением. Таким образом, первый этап решения, используя симплекс-метод, завершается нахождением допустимого базисного решения, хотя бы и неудачного.
На втором этапе производится последовательное улучшение найденного решения. При этом осуществляется переход от одного допустимого базисного решения к другому таким образом, чтобы значение
целевой функции улучшилось. Процесс решения, используя симплекс-метод, продолжается до тех пор, пока не будет достигнуто наименьшее (или наибольшее) значение функции цели. Геометрически это означает переход по ребрам из одной вершины многогранника допустимых значений в другую по направлению к той, в которой значение функции цели достигает экстремума.
Симплекс-метод дает оптимальную процедуру перебора базисных решений и обеспечивает сходимость к экстремальной точке за конечное число шагов. Используя симплекс-метод, вычисления на втором этапе ведутся по следующей схеме:
-
базисные переменные и функция цели выражаются через небазисные переменные;
-
по определенному правилу выбирается та из небазисных переменных, изменение значения которой способно улучшить значение F(x) , и она вводится в базис;
-
определяется, какая из базисных переменных должна быть выведена из базиса, при этом новый набор базисных переменных, образующийся на каждом шаге, отличается от предыдущего только одной переменной;
-
базисные переменные и функция цели выражаются через новые небазисные переменные, и повторяются операции b) и c).
-
Если на определенном шаге в симплекс-методе окажется, что изменение значений любой из небазисных переменных не может улучшить F(x) , то последнее базисное решение оказывается оптимальным.
-
Приведите основные шаги двойственного симплекс-метода.
Понятие
двойственности можно рассмотреть на
примере задачи оптимального использования
сырья. Пусть на предприятии решили
рационально использовать отходы
основного производства. В плановом
периоде появились отходы сырья m видов
в объемах
![]() единиц
единиц ![]() .
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск n
.
Из этих отходов, учитывая специализацию
предприятия, можно наладить выпуск n
видов
неосновной продукции. Через ![]() необходимо норму расхода сырья i-го вида
на единицу j-й
необходимо норму расхода сырья i-го вида
на единицу j-й
![]() продукции,
продукции,
![]() -
цена реализации единицы j-й продукции
(реализация обеспечена). Неизвестные
величины задачи:
-
цена реализации единицы j-й продукции
(реализация обеспечена). Неизвестные
величины задачи:
![]() —
объемы выпуска j-й
продукции, обеспечивающие предприятию
максимум выручки.
—
объемы выпуска j-й
продукции, обеспечивающие предприятию
максимум выручки.
Математическая модель задачи:
![]()
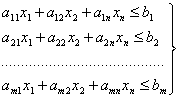
![]()
![]()
Предположим
далее, что с самого начала при изучении
вопроса об использовании отходов
основного производства на предприятии
появилась возможность реализации их
некоторой организации. Необходимо
установить прикидочные оценки (цены)
на эти отходы. Обозначим их![]() .
.
Оценки должны быть установлены исходя из следующих требований, отражающих несовпадающие интересы предприятия и организации:
-
общую стоимость отходов сырья покупающая организация стремится минимизировать;
-
предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП.
Требование 1 покупающей организации – минимизация покупки:
![]()
Требование 2 предприятия, реализующего отходы сырья, можно сформулировать в виде системы ограничений. Предприятие откажется от
выпуска
каждой единицы продукции первого вида,
если
![]() ,
где левая часть означает выручку за
сырье, идущее на единицу продукции
первого вида; правая – её цену.
,
где левая часть означает выручку за
сырье, идущее на единицу продукции
первого вида; правая – её цену.
Аналогичные рассуждения логично провести в отношении выпуска продукции каждого вида. Поэтому требование предприятия, реализующего отходы сырья, можно формализовать в виде сл. системы ограничений:
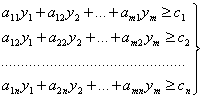
По смыслу задачи оценки не должны быть отрицательными:
![]() .
.
Переменны
![]()
![]() называют двойственными
оценками или объективно обусловленными
оценками.
называют двойственными
оценками или объективно обусловленными
оценками.
Задачи (2.23) - (2.25) и (2.26) - (2.28) называют парой взаимно двойственных ЗЛП.
Между прямой и двойственной задачами можно установить следующую взаимосвязь:
-
Если прямая задача на максимум, то двойственная к ней — на минимум, и наоборот.
-
Коэффициенты
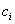 целевой функции прямой
задачи являются свободными членами
ограничений двойственной задачи.
целевой функции прямой
задачи являются свободными членами
ограничений двойственной задачи. -
Свободные члены
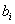 ограничений прямой
задачи являются коэффициентами целевой
функции двойственной.
ограничений прямой
задачи являются коэффициентами целевой
функции двойственной. -
Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу.
-
Если прямая задача на максимум, то ее система ограничений представляется в виде неравенств типа
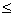 .
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа
.
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа
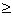 .
. -
Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой.
-
Все переменные в обеих задачах неотрицательны.
