23

ВВЕДЕНИЕ

В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций оказывается эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.

Язык программирования С# был создан в конце 1990-х годов и стал частью общей .NET-стратегии Microsoft. Впервые он увидел свет в качестве α-версии в середине 2000 года. С# непосредственно связан с С, C++ и Java. И это не случайно. Эти три языка — самые популярные и самые любимые языки программирования в мире. Более того, почти все профессиональные программисты сегодня знают С и C++, и большинство знает Java. Поскольку С# построен на прочном, понятном фундаменте, то переход от этих "фундаментальных" языков к "надстройке" происходит без особых усилий со стороны программистов. Кроме того, С# построен на улучшенной объектной модели, определенной в C++. Если вы знаете С или C++, то с С# вы сразу станете друзьями. С# и Java связаны между собой несколько сложнее. Как упоминалось выше, Java также является потомком С и C++. У него тоже общий с ними синтаксис и сходная объектная модель. Подобно Java C# предназначен для создания переносимого кода. Однако С# — не потомок Java. Скорее С# и Java можно считать двоюродными братьями, имеющими общих предков, но получившими от родителей разные наборы "генов".

Раздел 1 аппроксимация

При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться с корреляционной связью. При изучении количественных зависимостей различных показателей, значения которых определяются эмпирически, как правило, имеется некоторая их вариабельность. Частично она задается неоднородностью самих изучаемых объектов неживой и, особенно, живой природы, частично обуславливается погрешностью наблюдения и количественной обработкой материалов. Последнюю составляющую не всегда удается исключить полностью, можно лишь минимизировать ее тщательным выбором адекватного метода исследования и аккуратностью работы. Поэтому при выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей, этой или иной степени замаскированных неучтенностью вариабельности значений. Для этого и применяется аппроксимация - приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости.

1.1 Аппроксимация

Аппроксимация (от латинского «approximate» - «приближаться») – приближенное выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов.

Как известно, между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости. Поэтому важно считывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда.

При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, многопараметрическое уравнение. Однако нет никакого смысла стремиться с максимальной точностью передать случайные отклонения величин в конкретных рядах эмпирических данных. Гораздо важнее уловить общую закономерность, которая в данном случае наиболее логично и с приемлемой точностью выражается именно двухпараметрическим уравнением степенной функции. Таким образом, выбирая метод аппроксимации, исследователь всегда идет на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных. Наряду с выявлением закономерностей, замаскированных случайными отклонениями эмпирических данных от общей закономерности, аппроксимация позволяет также решать много других важных задач: формализовать найденную зависимость; найти неизвестные значения зависимой переменной путем интерполяции или, если это допустимо, экстраполяции.

1.2 Интерполяция

Интерполяция (частный случай аппроксимации), интерполирование в вычислительной математике способ нахождения промежуточных  значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных  экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Способы интерполяции:

1. Интерполяция методом ближайшего соседа. Это простейший способ интерполяции.

2. Интерполяция многочленами. На практике чаще всего применяют интерполяцию многочленами. Это связано, прежде всего, с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов в плотном пространстве непрерывных функций (теорема Вейерштрасса):

• линейная интерполяция;

• интерполяционная формула Ньютона;

• метод конечных разностей;

• ИМН-1 и ИМН-2;

• многочлен Лагранжа (интерполяционный многочлен);

• по схеме Эйткена;

• сплайн-функция;

• кубический сплайн.

3. обратное интерполирование (вычисление x при заданном y):

• полином Лагранжа;

• обратное интерполирование по формуле Ньютона;

• обратное интерполирование по формуле Гаусса.

4. интерполяция функции нескольких переменных:

• билинейная интерполяция;

• бикубическая интерполяция.

5. другие способы интерполяции:

• рациональная интерполяция

• тригонометрическая интерполяция

Для заданных N точек N>>1 интерполяция может быть локальной или глобальной. Глобальная – использует все заданные точки, а локальная -выполняется по нескольким соседним точкам.

Таблица 1.1 Виды интерполяции

Интерполяция
локальная				глобальная
линейная	параболическая	кубическая парабола	полином степени (N-1)		кубический сплайн

В таблице 1.1 показаны три самых распространенных вида локальной интерполяции (линейная, параболическая, кубическая) и два глобальной: полином степени (N-1) и кубический сплайн.

К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.

1.3 Полином Лагранжа

Интерполяционный многочлен Лагранжа – многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x₀,y₀),(x₁,y₁)….,(x_n,y_n), где все x_j различны, существует единственный многочлен L(x) степени не более n, для которого L(x_j)=y_j.

В простейшем случае (n-1) – это линейный многочлен, графиккоторого.– прямая, проходящая через две заданные точки.

Лагранж предложил способ вычисления таких многочленов:

L(x)=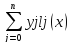(1.1)

где базисные полиномы определяются по формуле:

l_j(x)=(1.2)

Полином Лагранжа интенсивно используются в прикладной математике. Но у него есть и совсем другие применения. Полиномы Лагранжа помогают доказать следующие классические теоремы из чистой математики:

1. конечная коммутативная группа матриц над полем K приводится к диагональному виду (здесь дополнительно нужно требовать, чтобы поле K содержало все корни k-ой степени из единицы, где k – порядок группы, и чтобы k не делилось на характеристику поля K).

2. алгебраическое уравнение степени.

Достоинства и недостатки интерполяционных формул Лагранжа:

• достоинство – метод наиболее прост в понимании и организации вычислительного процесса. Основной недостаток метода – при увеличении числа узлов и соответственно степени интерполяционный многочлен Лагранжа требуется строить заново.

• достоинство – метод относится к числу итерационных методов и имеет наибольшую точность интерполяции. Основной недостаток метода – медленная скорость сходимости, что приводит к значительным затратам машинного времени.

• достоинство – использование многочленов невысокого порядка и вследствие этого малым накоплением погрешностей в процессе вычислений.

Интерполяционный многочлен Лагранжа имеет существенный недостаток: если при выбранном числе узлов выяснилось, что интерполяционный многочлен недостаточно точно находит значение функций в заданной точке, то при добавлении одного или нескольких узлов все вычисления необходимо проводить заново. В этом случае, когда требуется найти не аналитическое выражение, а лишь его значение в некоторой точке, от этого недостатка можно избавиться.

1.4 Подбор эмпирических формул

При интерполировании функций используется условие равенства значений интерполяционного многочлена и данной функции в известных точках – узлах интерполяции. Это предъявляет высокие требования к точности данных значений функции. В случае обработки опытных данных, полученных в результате наблюдений или измерений, нужно иметь в виду ошибки этих данных. Они могут быть вызваны несовершенством измерительного прибора, субъективными причинами, различными случайными факторами и т. д. Ошибки экспериментальных данных можно условно разбить на три категории по их происхождению и величине: систематические, случайные и грубые.

Таким образом, в экспериментальных данных всегда имеются случайные ошибки. Они, вообще говоря, могут быть уменьшены до сколь угодно малой величины путем многократного повторения опыта. Однако это не всегда целесообразно, поскольку могут потребоваться большие материальные или временные ресурсы. Значительно дешевле и быстрее можно в ряде случаев получить уточненные данные хорошей математической обработкой имеющихся результатов измерений.

В частности, с помощью статистической обработки результатов измерений можно найти закон распределения ошибок измерений, наиболее вероятный диапазон изменения искомой величины (доверительный интервал) и другие параметры.

Пусть, изучая неизвестную функциональную зависимость между у и х, в результате серии экспериментов произвели ряд измерений этих величин и получили таблицу значений.

Таблица 1.2 Таблица значений

x0	x1	…	xn
y0	y1	…	yn

Задача состоит в том, чтобы найти приближенную зависимость y = f (x), значения которой при х = x_i, (i = 0, 1, ..., n) мало отличаются от опытных данных y_i. Приближенная функциональная зависимость, полученная на основании экспериментальных данных, называется эмпирической формулой.

Построение эмпирической формулы состоит из двух этапов:

1) подбор общего вида этой формулы;

2) определение наилучших значений содержащихся в ней параметров.

По экспериментальным точкам строится диаграмма рассеивания. Если последовательность точек диаграммы рассеивания группируется в виде некоторой линии, то можно сделать предположение о наличии связи. Затем проводят выбор формы связи путем сравнения внешнего вида диаграммы рассеивания с имеющимися математическими моделями. Линия, которая описывает диаграмму рассеивания, называется линией регрессии, а описывающее ее уравнение – уравнением регрессии. Процесс нахождения теоретической линии регрессии называют выравниванием эмпирической линии регрессии.

1.5 Метод наименьших квадратов

Пусть тип эмпирической формулы выбран, и ее можно представить в виде:

у =  (х, а₀, а₁, ..., а_m ), (1.3)

где  – известная функция;

а₀, а₁, ..., а_m – неизвестные постоянные параметры.

Задача состоит в том, чтобы определить такие значения этих параметров, при которых эмпирическая формула дает хорошее приближение данной функции, значения которой в точках x_i равны y_i (i = 0, 1, …, n ).

Здесь не ставится условие (как в случае интерполяции) совпадения опытных данных у_i со значениями эмпирической функции в точках x. Разность между этими значениями (отклонения) обозначим через _i. Тогда

_i =  (x_i, а₀, а₁, ..., а_m ) – y_i, i = 0, 1, …, n. (1.4)

Задача нахождения наилучших значений параметров а₀, а₁, ..., а_m сводится к некоторой минимизации отклонений e_i. Существует несколько способов решения этой задачи: метод выбранных точек, метод средних и метод наименьших квадратов.

Метод выбранных точек и метод средних являются сравнительно простыми, однако в ряде случаев получаемые с их помощью аппроксимации не обладают достаточной точностью.

Метод наименьших квадратов. Запишем сумму квадратов отклонений для всех точек х₀, х₁, ..., х_п:

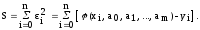(1.5)

Параметры а₀, а₁, ..., а_m эмпирической формулы будем находить из условия минимума функции S = S (а₀, а₁, ..., а_m). В этом состоит метод наименьших квадратов.