7. О приведении матрицы преобразования к диагональному виду.

Предложение 8. Матрица линейного преобразования в базисеимеет диагональный видвсе векторы базиса – собственные векторы преобразования.

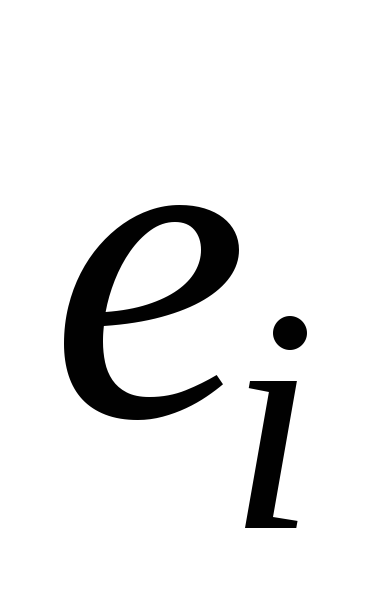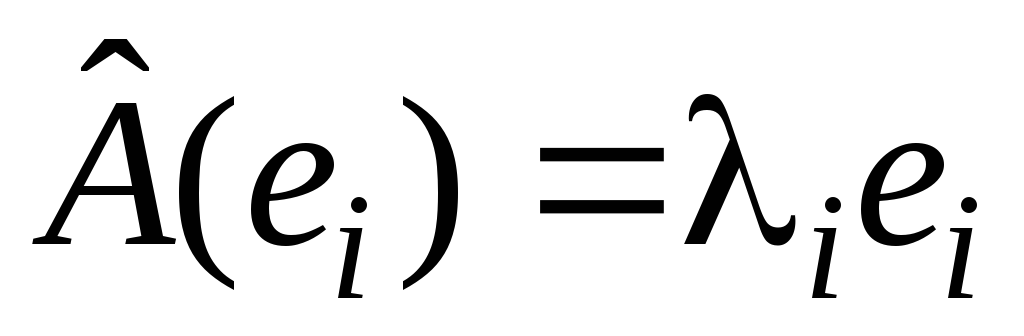
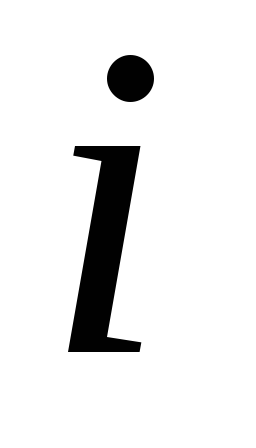Доказательство. Действительно, если - собственный, то-ый элемент столбца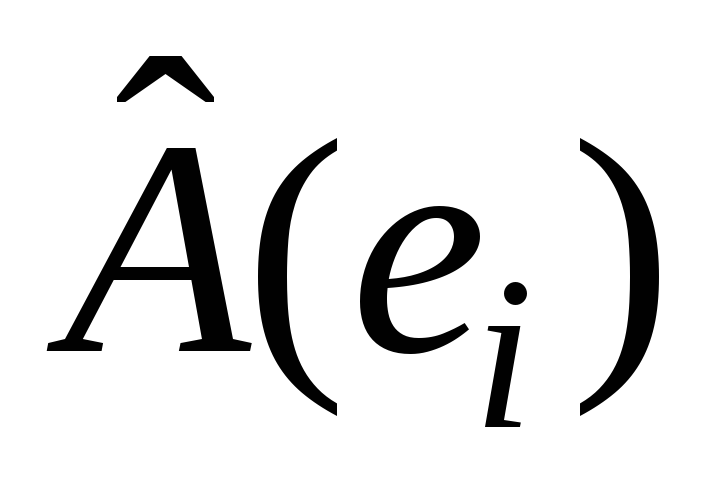, равен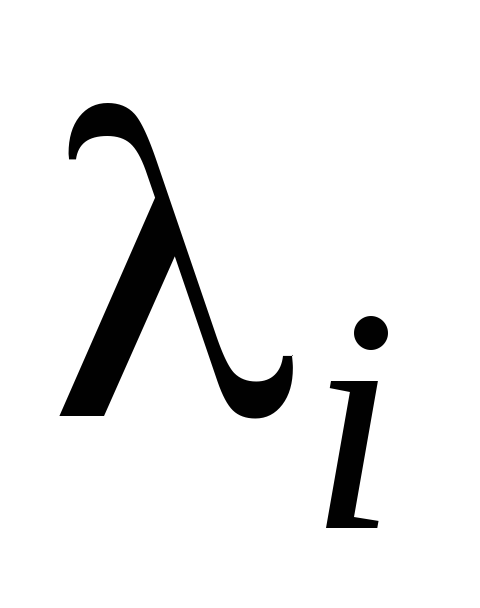, а остальные равны нулю. Обратно, аналогично. ■

Предложение 9. Если преобразование имеет и попарно различных собственных значений, то существует базис из собственных векторов этого преобразования.

Доказательство. Следует из теоремы 4.

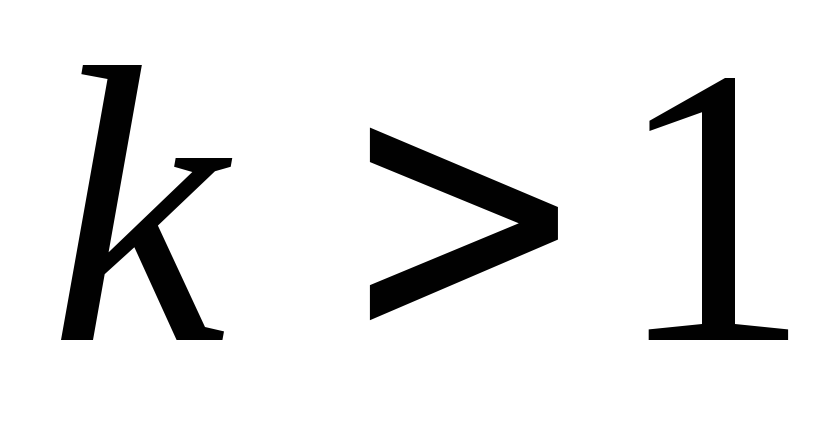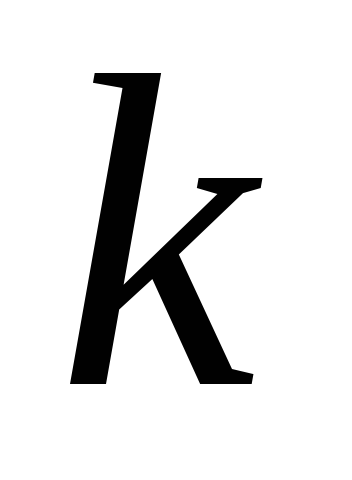Может оказаться, что собственное значение имеет кратность , но существуетлинейно независимых собственных векторов.