§ 13. Билинейные и квадратичные функции на евклидовых пространствах.

1º. Преобразование, присоединенное к билинейной функции.

Пусть – евклидово пространство, b(x,y) – билинейная функция на.

Def 1. Линейное преобразование Â на называется присоединенным к билинейной функции b(x,y), если выполнено

b(x,y)=(x ,Ây). (1)

Утверждение 1. Каждая билинейная функция имеет присоединенное преобразование, и такое преобразование единственно.

Доказательство. Пусть - базис в и А – матрица Â в этом базисе. Тогда

(x,Ây)=ХГAY,

где Г – матрица Грама в базисе , Х,Y – координатные столбцы x и y, следовательно, (x,Ây) – билинейная функция с матрицей ГА. В силу единственности матрицы билинейной функции в базисе имеем, что если у билинейной функции b(x,y) существует присоединенное преобразование, то матрица В билинейной функции равна

В=ГА.

Отсюда следует

А=.

Это означает, что билинейная функция не может иметь больше одного присоединенного преобразования: если оно существует, то его матрице равна .

Докажем существование присоединенного преобразования. Для этого надо проверить, что преобразование с матрицей (2) является присоединенным. Действительно, если (x,Ây)= ХГAYХГY= b(x,y). ■

Формула (3) – это формула связи между матрицами билинейной функции и линейного преобразования, следовательно, если базис ортонормированный, то

А=В.

Если А – симметричная, то Â – самосопряженный оператор

Следствие. Присоединенное преобразование является самосопряженным билинейная функция является симметричной.

Преобразование, присоединенное к симметричной билинейной функции, называется присоединенным к соответствующей квадратичной форме.

2º. Ортонормированный базис, в котором квадратичная форма имеет диагональный вид.

Теорема1. В евклидовом пространстве для каждой квадратичной формы существует ортонормированный базис, в котором она имеет диагональный вид.

Доказательство. Базисом, существование которого утверждается, является ортонормированный базис из собственных векторов самосопряженного преобразования, присоединенного к квадратичной форме. В нем В=А и А – диагональная матрица. ■

Следующая теорема является по существу другой формулировкой теоремы 1.

Теорема 2. Пусть в линейном пространстве L заданы две квадратичные формы k и h, причем h положительно определенная. Тогда в L существует базис, в котором обе формы имеют диагональный вид.

Для доказательства введем в L скалярное произведение, приняв h за основную квадратичную форму. По отношению к этому скалярному произведению ортонормированными будут те базисы, в которых h имеет канонический вид. По теореме 1 для формы k существует ортонормированный базис, в котором она имеет диагональный вид. Это и есть базис, существование которого мы доказываем.

Замечание. Если пространство L евклидово, то теорема 2 останется, конечно, справедливой. Уже существующее скалярное произведение оставляется без внимания, а для доказательства вводится новое скалярное произведение при помощи формы h. Найденный базис, вообще говоря, не будет ортонормированным по отношению к старому скалярному произведению.

Теперь приведем две квадратичные формы к диагональному виду в одном и том же базисе. Пусть K и H – матрицы квадратичных форм в исходном базисе е. Матрица H является матрицей Грама базиса е для вспомогательного скалярного произведения. Поэтому преобразование, присоединенное к форме k в базисе е, имеет матрицу . Напишем его характеристический многочлен в виде . Так как , характеристическое уравнение имеет те же корни, что и уравнение

, (5)

называемое обобщенным характеристическим уравнением. Для каждого из его корней система уравнений собственного подпространства эквивалентна системе

.

Для каждого корня фундаментальную систему решений такой системы уравнений надо ортогонализовать и нормировать, находя скалярное произведение по формуле с матрицей Грама H. Объединяя все так полученные ортонормированные базисы собственных подпространств, мы получаем базис . Он ортонормирован относительно вспомогательного скалярного произведения, и потому форма h в нем имеет канонический вид. Так как он состоит из собственных векторов преобразования, присоединенного к k, эта форма будет иметь диагональный вид в базисе .

Пример. Найти матрицу перехода к базису, в котором квадратичные формы

,

обе имеют диагональный вид, а также их вид в этом базисе.

Решение. Здесь - т.е. положительно определенная. Таким образом, билинейную форму, соответствующую , можно взять за скалярное произведение.

Матрица этой билинейной формы имеет вид: , т.е. она является матрицей Грама в соответствующем евклидовом пространстве. Тогда матрица присоединенного преобразования к билинейной форме , соответствующая , имеет вид

.

Найдем собственные значения А:

~~

.

Нормировка по скалярному произведению с :

. .

. .

Таким образом, и выбираем за новый базис, т.е. .

Тогда , .

.
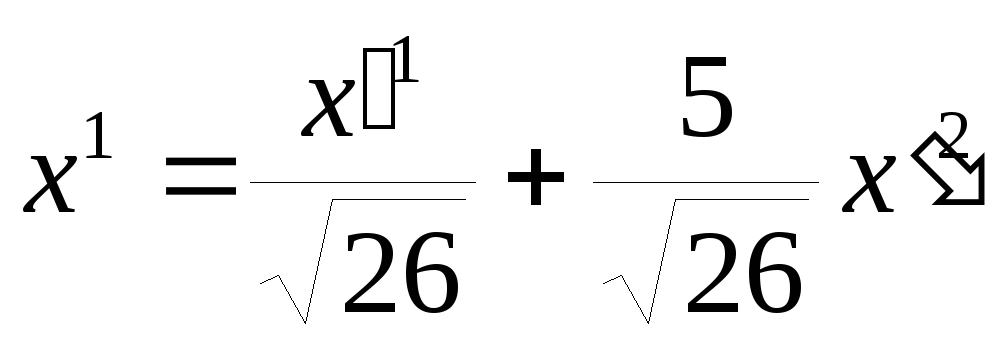
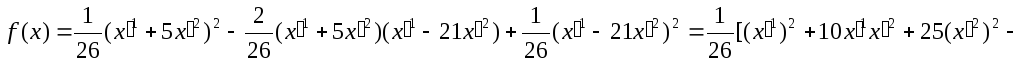