Уравнения максвелла

Введение двух гипотез о существовании вихревого электрического поля и тока смещения позволили Максвеллу создать единую теорию электромагнетизма. В основе этой теории находятся четыре уравнения, названные уравнениями Максвелла, которые играют в учении об электромагнетизме такую же роль, как законы Ньютона в классической механике. Рассмотрим эти уравнения.

1. Первое уравнение. Согласно (10), циркуляция напряжённости вихревого электрического поля равна

(16)

Но Тогдагде (— проекция производной по времени индукции магнитного поля на направление нормалик площади контура. Поскольку в общем случае индукция магнитного поля зависит от координат и времени, тонадо заменить частной производной. С учётом этого уравнение (16) запишется

(17)

Из этого уравнения следует, что источником электрического поля является изменяющееся со временем магнитное поле.

2. Второе уравнение. Максвелл обобщил закон полного тока, введя в её правую часть полный ток , гдеS  площадь замкнутого контура длиною l. Учитывая это, закон полного тока запишется

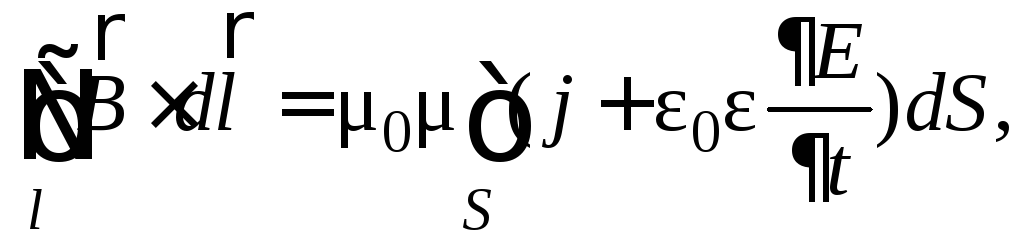(18)

поскольку Это уравнение показывает, что магнитное поле может создаваться как движущимися зарядами (электрическим током), так и переменным электрическим полем.

3. В качестве третьего и четвертого уравнений Максвелл взял теорему Гаусса для электростатического и магнитного полей

(19) (20)

Соотношение (19) свидетельствует о том, что линии напряжённости электростатического поля начинаются и кончаются на электрических зарядах, а из (20) следует, что линии магнитной индукции всегда замкнуты, т.е. в природе не существует магнитных зарядов. Необходимо отметить, что нумерация уравнений Максвелла произвольная.

Из уравнений (17) и (18) вытекает, что переменное магнитное поле всегда связано с создаваемым им электрическим полем, и наоборот, переменное электрическое поле связано с создаваемым им магнитным полем. Таким образом, эти поля взаимосвязаны и образуют единое электромагнитное поле. Поэтому отдельное рассмотрение электрических и магнитных полей носит относительный характер. Так, например, если электрическое поле создаётся неподвижными зарядами в одной системе отсчёта, то относительно другой они могут двигаться и, следовательно, порождают одновременно и электрическое и магнитное поля. Уравнения Максвелла являются основой единой теории электрических и магнитных явлений.

7