§8. Работа сил электростатического поля при перемещении заряда.

При движении зарядов в электрическом поле силы, действующие на него со стороны поля, совершают работу. Пусть в начальный момент времени заряд находится в точке 1, определяемой радиус-вектором а затем по произвольной траектории он перемещается в точку2 с радиус-вектором РаботуA₁₂, совершаемую силой находим по формуле: . Из рис. 4 видно, что dlcos = dr, где dr  проекция dl на направление радиус-вектора , т.е. элементарное приращение модуля радиус-вектора. С учётом этого 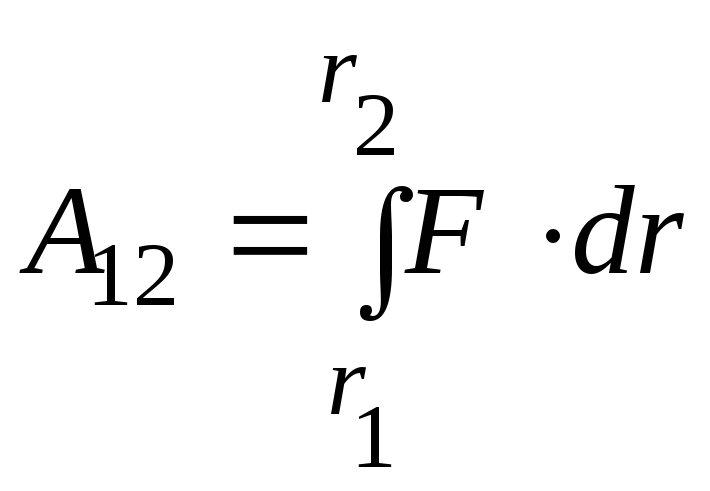. В данном случае на зарядq₀ действует кулоновская сила Подставляя это выражение в предыдущую формулу, получаем:

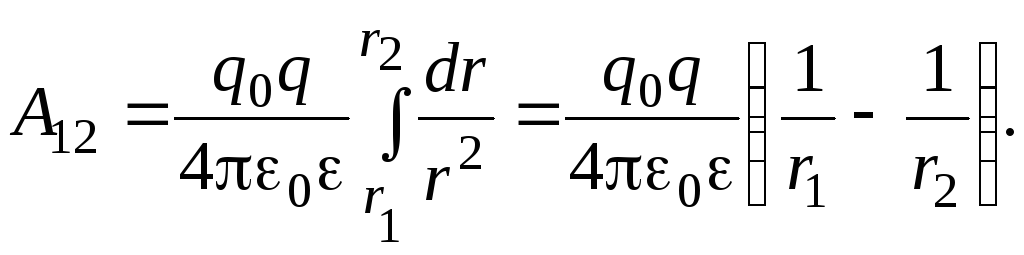(13)

Р

dr



2

1

q

q₀

ис. 4

Из полученного соотношения видно, что работа сил электростатического поля, создаваемого точечным зарядом, определяется только начальным и конечным положением заряда, и, следовательно, не зависит от формы траектории движения. Оказывается, что этим свойством обладает любое электростатическое поле, а не только поле точечного заряда. Следовательно, электростатическое поле является потенциальным.

Циркуляция напряжённости электрического поля

Из выражения (13) следует также, что при переносе заряда по замкнутому пути, т.е., когда заряд возвращается в исходное положение, r₁ = r₂ и A₁₂ = 0. Тогда запишем . Значок_ на интеграле означает, что интегрирование производится по замкнутой кривой. Но сила ,действующая на заряд q₀, равна . Поэтому последнюю формулу перепишем в виде: Разделив обе части этого равенства наq₀, находим:

(14)

Выражение вида называется циркуляцией напряжённости электрического поля. Как указывалось, электростатическое поле потенциально. Для него циркуляция напряжённости равна нулю. Поэтому формулу (14) рассматривают как условие потенциальности поля.

7