Лекция №3 энергия. Работа аналогия между вращательным и поступательным движением

Рассмотрев поступательное и вращательное движения можно установить аналогию между ними. В кинематике поступательного движения используются путь s, скорость  и ускорение а. Их роль во вращательном движении играют угол поворота , угловая скорость  и угловое ускорение ε. В динамике поступательного движения применяются понятия силы , массыт и импульса Во вращательном движении роль силы играет моментсилы, роль массы — момент инерцииI_z и роль импульса — момент импульса Зная формулы поступательного движения легко записать формулы вращательного движения. Например, при равномерном движении пройденный путь вычисляется по формуле:s =t, а при вращательном угол поворота — по формуле  = t. 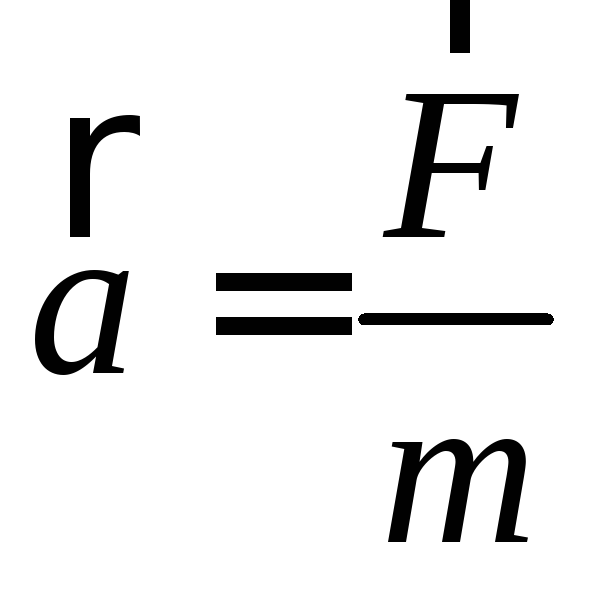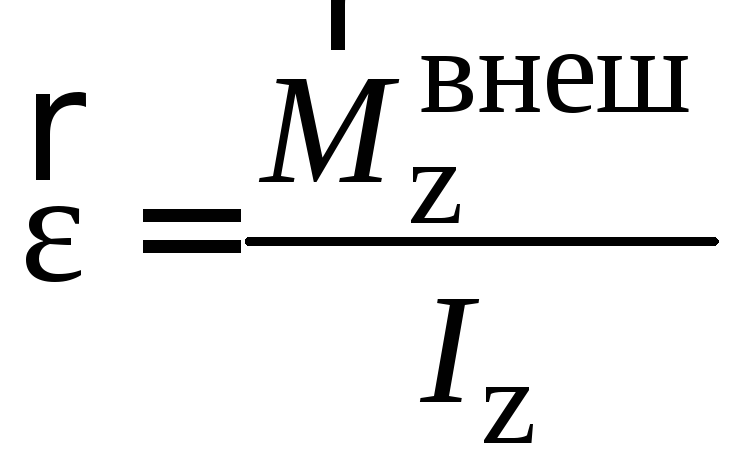Второй закон Ньютона иа основной закон динамики вращательного движения —и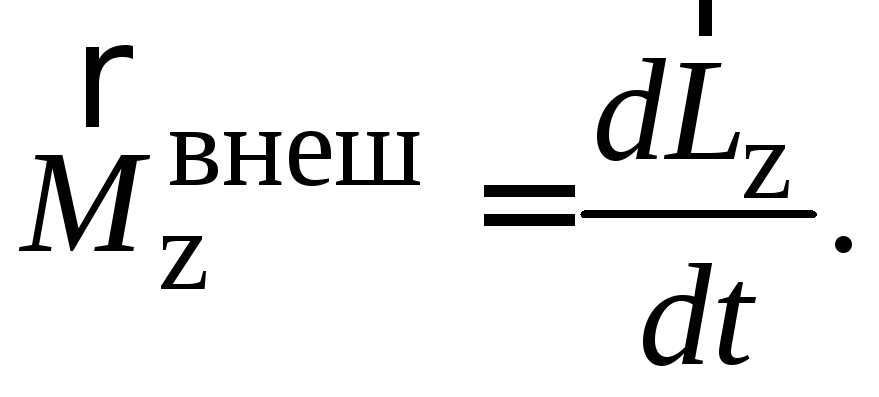При поступательном движении импульс тела равена при вращательном движении момент импульса —Эту аналогию можно продолжать и дальше.

Работа силы при поступательном движении. Мощность

Пусть тело (материальная точка) под действием постоянной силы , составляющей неизменный уголс направлением перемещения, движется прямолинейно в некоторой системе отсчёта и проходит путьl. Тогда, как известно из школьного курса физики, работаAэтой силы находится по формуле:

A = Fl·cos  = F_l l, (1)

Рассмотрим теперь общий случай вычисления работы, когда тело движется поступательно по криволинейной траектории под действием переменной силы. На пути l выделим элементарный участок dl, в пределах которого можно считать силу и угол неизменными величинами, а сам участок — прямолинейным. Тогда работу dA на этом участке найдём, используя формулу (1): dA = F·dl·cos. Работа A на всём пути равна сумме работ dA, т.е.

(2)

Значок l при интеграле означает, что интегрирование производится по всему пути l.

Формуле (2) можно придать иной вид, если воспользоваться скалярным произведением векторов. Тогда подынтегральное выражение dAзапишется в виде:dA = F·dl·cos= где — вектор элементарного перемещения, и

(3)

Из формулы (1) видно, что работа является алгебраической величиной. Знак работы зависит от угла . Если угол  острый, то cos  > 0 и работа положительная, если же угол  тупой — отрицательная.

В системе единиц СИ единицей работы является джоуль (Дж). Она вводится из формулы (1), в которой полагают cos  = 1. 1 Дж — это работа, которую совершает сила в 1 Н на пути 1 м при условии совпадения направлений силы и перемещения.

Для характеристики быстроты совершения работы вводится понятие мощности, равной работе, совершённой в единицу времени. Если элементарный промежуток времени dt совершается элементарная работа dA, то мощность Р равна

(4)

В системе единиц СИ мощность измеряется в ваттах (Вт). Как следует из (4), 1 Вт = 1 Дж / 1 с, т.е. 1 Вт — это мощность, при которой за 1 с совершается работа в 1 Дж.

Работа силы при вращательном движении

Рассмотрим твёрдое тело, которое под действием переменной силы поворачивается вокруг осиzна некоторый угол. Эта сила создаёт момент силМ_z, вращающий тело. Сила направлена по касательной к окружности, по которой движется точка приложения силы. Поэтому угол= 0. Учитывая это, по аналогии с формулой механической работы (см. (2)), находим выражение, по которому вычисляется работа при вращательном движении:

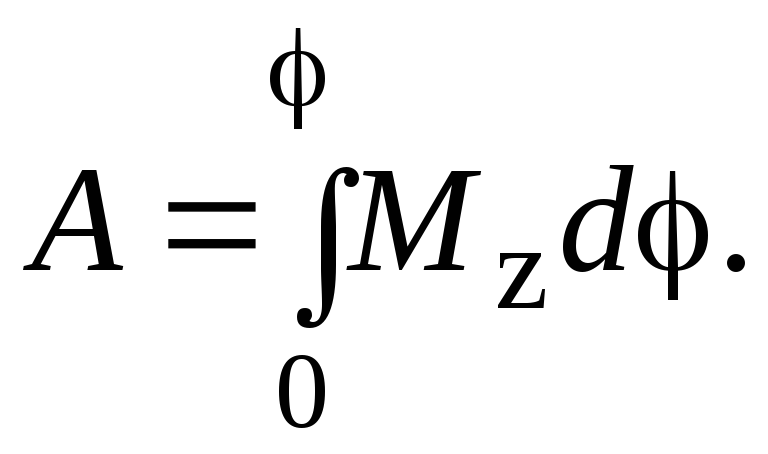(5)

Работа будет положительной, если направление касательной составляющей силы совпадает с направлением вращения, и отрицательной — при их противоположном направлении.