
- •3.Неконпенсированная теплота
- •12 Скорость хим реакции методы измерения
- •13.Закон формальной кинетики
- •14 Порядок рекций
- •15.Методы определения порядка,время полупревращения
- •21.Методы определения степени диссоциации
- •Методы определения
- •25. Поверхностная энергия Гиббса,Поверхностное натяжение
- •26.Уравнение изотрмы,абсорции Гибсса
- •Изотерма химической реакции (изотерма Вант-Гоффа)
- •27.Адсорбция на твердых абсольвентах
- •28. Теория адсорбции.Газовая храмотография
2.Постулат локального равновесия


6.Ур-е Баланса


5.Потоки и силы


4.Скорость возн энтропии
Вообще скорость прироста энтропии внутри системы равна сумме членов, представляющих скорость возникновения энтропии в системе и скорость оттока энтропии. [1]
Подчеркнем еще раз, что основным понятием термодинамики неравновесных процессов является скорость возникновения энтропии а. Однако в связи с неясностью физического содержания б Q это понятие в дальнейшем не используется. [2]
Подчеркнем еще раз, что основным понятием термодинамики неравновесных процессов является скорость возникновения энтропии о. Впрочем, в связи с неясностью физического содержания 6Q можно постепенно от него отходить, заменяя, как мы уже это и делали, возникновением энтропии. [3]
Скорость возникновения энтропии представляет собой сумму двух членов: скорости возникновения энтропии системы и скорости возникновения энтропии термостата. [4]
Стационарное слабо-неравновесное состояние открытой системы, в которой происходит необратимый процесс, характеризуется тем, что скорость возникновения энтропии имеет минимальное значение при данных внешних условиях, препятствующих достижению системой равновесного состояния. Под текущим равновесием понимают стационарное неравновесное состояние открытой системы, устойчивое по отношению к малым отклонениям. [5]
Стационарное же слабонеравновесное состояние открытой системы, в которой происходит неравновесный процесс, характеризуется тем, что скорость возникновения энтропии имеет минимальное значение при данных внешних условиях, препятствующих достижению системой равновесного состояния - это обусловливает максимальную структурированность открытой неравновесной системы ( согласованность поведения подсистем) при данных граничных условиях. Другими словами, система находится в состоянии с минимальным производством энтропии, характеризующимся много меньшим значением энтропии составляющих ее частиц ( подсистем), чем энтропия системы, находящейся в равновесном состоянии. [6]
Полученное уравнение показывает, что скорость изменения энтропии системы равняется скорости обмена энтропией между системой и окружающей средой плюс скорость возникновения энтропии внутри системы. [7]
Это соответствует, можно сказать, эффекту насыщения по отношению к сродству, и в области, где этот эффект проявляется, скорость возникновения энтропии становится согласно (14.17) и (14.18) линейной функцией сродства. [8]
Если оперировать единственно общепринятыми в настоящее время терминами кинетическая и диффузионная области, то следует все физико-химические процессы разбить на две неравные группы. При этом термин кинетическая область обозначает, что скорость возникновения энтропии лимитируется скоростью химического взаимодействия. Термин же диффузионная область означает, что скорость возникновения энтропии лимитируется скоростью одного из физических процессов. Вопрос о том, какой именно из физических процессов является в этом случае лимитирующей стадией, представляет самостоятельную задачу. Практически кинетическая область имеет место, когда все физические процессы протекают вблизи от равновесия. Обычно при этом имеют в виду наличие теплового и фазового равновесия. Диффузионная же область имеет место вблизи от положения химического равновесия в реакционной фазе. [9]
Для получения выражения Д5 в явном виде используем выражения для скорости возникновения энтропии 0 и потоков J в общем виде, известные как линейные законы Онзагера. [10]
Энтропия в естественных процессах непрерывно возрастает. Скорость возрастания энтропии системы плюс скорость оттока энтропии должна равняться скорости возникновения энтропии внутри системы. [11]
Для получения выражения А5 в явном виде используем выражения для скорости возникновения энтропии 9 и потоков J в общем виде, известные как линейные законы Онзагера. [12]
Как видно в уравнении ( II, 7) имеется, в отличие от уравнений непрерывности, добавочный член 9, выражающий возникновение энтропии внутри области. Все уравнение читается так: скорость роста энтропии в данном объеме равна разности между скоростью возникновения энтропии в данной области и скоростью оттока энтропии из области. J Qdv и обусловлена необратимыми процессами внутри системы. Следует обратить внимание [16], что величина 0 обращается в нуль, если становятся равными нулю градиенты химического потенциала и температуры. Именно эти градиенты обусловливают развитие процессов, связанных с ростом энтропии. [13]
С энтропией дело обстоит сложнее. Энтропия в общем случае не сохраняется, она может возникать внутри выделенного объема, и поэтому уравнение, выражающее баланс энтропии, должно содержать член, выражающий скорость возникновения энтропии внутри выделенной области. Пусть s обозначает энтропию единицы массы. [14]
В этом случае соблюдается принцип взаимности Онзагера между термодинамическими силами и потоками. При трении все процессы ( изнашивание, тепловыделение, трибоэлектризация, диффузионные и магнитные потоки и др.) являются необратимыми и могут оцениваться различными энтропийными потоками. Пригожину, при стационарном состоянии системы скорость возникновения энтропии становится постоянной и минимальной при заданных постоянных параметрах внешнего воздействия. [15]
3.Неконпенсированная теплота
Некомпенсированная теплота, деленная на Т, и дает величину возникновения энтропии в системе. [1]
Некомпенсированная теплота принципиально отличается от использованной ранее ( § 5) внутренней теплоты Q. Знак Q зависит от повышения или понижения температуры системы в процессе. При релаксации в изолирован-ной системе температура может понижаться, но некомпенсированная теплота Qln всегда выделяется. [2]
Всегда положительную некомпенсированную теплоту dQ необходимо отвести от системы и для поддержания постоянства температуры. [3]
Возникновение некомпенсированной теплоты связано с дополнительным возрастанием энтропии. [4]
Последнее соотношение связывает некомпенсированную теплоту с так называемым возникновением энтропии ( dtS) в системе вследствие протекающих в ней неравновесных процессов. [5]
Последнее соотношение связывает некомпенсированную теплоту с так называемым возникновением энтропии ( dfS) в системе вследствие протекающих в ней неравновесных процессов. [6]
Последнее соотношение связывает некомпенсированную теплоту с так называемым возникновением энтропии ( djS) в системе вследствие протекающих в ней неравновесных процессов. [7]
Последнее соотношение связывает некомпенсированную теплоту с так называемым возникновением энтропии ( d / S) в системе вследствие протекающих в ней неравновесных процессов. [8]
Очевидно, что если некомпенсированная теплота равна нулю, процесс обратим; при конечном значении некомпенсированной теплоты процесс будет необратимым. Обратимый процесс можно проводить в прямом и обратном направлениях, и при этом все переменные в обратном процессе проходят те же значения в обращенной последовательности, что и в прямом. [9]
Пригожий [2, 3], считающий термин некомпенсированная теплота неудачным, подчеркнул, что некомпенсированная теплота dQ возникает вследствие протекания необратимых процессов внутри самой системы, тогда как dQ относится к обмену энергией с внешней средой. [10]
Теряемая работа оказывается пол тому просто равной некомпенсированной теплоте, и мы скова приходим к основному неравенству дс Допде. Итак, метод Шоттки, Улиха и Вагеера приводит к тем же самым результатам, что и используемый нами, однако их метод необходимо требует сопоставления каждого реального необратимого изменения с неким гипотетическим обратимым процессом. [11]
S const и v const), некомпенсированная теплота равна убыли внутренней энергии. В то же время эта убыль в соответствии с критериями самопроизвольности, рассматриваемыми и в общей термодинамике, является критерием неравновесности процесса. [12]
В связи с этим величину dQ Клаузиус назвал некомпенсированной теплотой независимо от физической природы работы, которая может быть механической, электрической или магнитной. [13]
Как будет видно дальше, соотношения (9.16) и (9.17) позволяют связать некомпенсированную теплоту с сродством химической реакции, к предварительному рассмотрению которой мы сейчас и подойдем. [14]
Если химическая реакция является единственной причиной необратимости процесса в системе, тонекомпенсированная теплота и соответствующее возникновение ( скорость) энтропии зависят только от интенсивности протекания реакции. [15]
8.Ур-е Оизагера
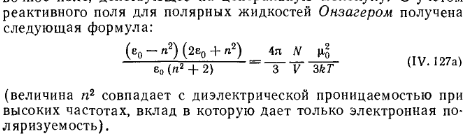

9.Перенос через барьер
В качестве примера применения методов термодинамики необратимых процессов рассмотрим перенос вещества через барьер. Пусть сосуд, содержащий некоторый газ, разделен перегородкой, поглощающей этот газ. При этом газ способен растворяться в этой перегородке. Будем поддерживать разность температур ΔT по обе стороны перегородки. Следует выяснить величину Δp (разность давлений газа по обе стороны перегородки), вызванную наличием разности температур ΔT, и определить, в каких случаях Δp имеет место.
Каждую задачу, которую трактует термодинамика необратимых процессов, без рассмотрения механизма процесса, можно решить и без применения термодинамики необратимых процессов на основе анализа механизма.
Рассмотрим физику обсуждаемой задачи. Пусть давление газа будет мало и раствор его в материале перегородки будет разбавленным. Тогда, согласно закону Генри, с = гр, где с - концентрация растворенного вещества, р - давление. Из этого уравнения непосредственно следует, что величины с на противоположных сторонах перегородки будут разными. Если растворимость растет с температурой (Qраств < 0), то растворимость в более нагретой стороне перегородки будет больше и по перегородке начнется диффузия газа от горячей стороны перегородки к холодной. Это будет приводить к повышению давления в холодной половине сосуда и уменьшению его в горячей. Так будет возникать перепад давления Δp. Процесс перехода вещества прекратится, когда влияние Δp на растворимость компенсирует влияние ΔT и величина с станет одинаковой на обеих сторонах перегородки.
536
Из этого рассмотрения следует, что Δр будет возникать, если Qраствор ≠ 0. Легко найти связь между Δр и ΔT. Действительно, постоянство с означает гр = const или гΔр + рΔг = 0. Следовательно, Δр/р = -Δг/г или, дифференцируя по температуре:
d ln p/dT = - d ln г/dT, но d ln г/dT = - Qраств/RT2 (см. гл. V), тогда
d ln p/dT = Qраств/RT2. (XX.3)
Так как pυ = RT, то уравнение (ХХ.3) может быть переписано следующим образом:
dp/dT = Qраств/Tυ. (ХХ.4)
Из этого уравнения видно, что Δр и ΔT имеют одинаковые знаки, если Qраств > 0.
Методы термодинамики необратимых процессов позволяют вывести уравнение (ХХ.4) без анализа механизма процесса.
Применим метод Онзагера для решения задачи переноса через барьер.
В рассматриваемой системе осуществлены два градиента, и это означает, что действуют две силы - тепловая и химическая. Тогда термодинамические уравнения движения будут иметь вид:
J1 = L11X1 + L12X2; J2 = L21X1 + L22X2. (XX.5)
Пусть индексом 1 обозначены перенос тепла и тепловая сила, а 2 - перенос вещества и химическая сила. В стационарном состоянии нет потока вещества и J2 = 0. Отсюда X2/X1 = -L21/L22, но так как
X1 = -(1/T)gradT, а X2 = -Tgrad(μ/T), то
|
X2 |
|
X1 |
=
|
d(μ/T) |
|
dT |
T2 и
|
L21 |
|
L22 |
= -
|
d(μ/T)T2 |
|
dT |
.
Учтем, что
|
d(μ/T) |
|
dT |
=
|
Tdμ - μdT |
|
T2 |
,
а также, что dμ = - SdT + υdp и μ = H - TS.
тогда -
|
в(μ/T) |
|
dT |
=
|
H - υT(dp/dT) |
|
T2 |
Отсюда следует, что
L21/L22 = H - υT(dp/dT). (XX.6)
537
Смысл левой части этого равенства можно понять, если рассмотреть перенос тепла на один моль вещества (J1/J2) в отсутствие градиента температуры (X1 = 0).
В этом случае из (ХХ.5) получим
J1/J2 = L12/L22. (XX.7)
Согласно второму постулату, L12 = L21. Из формул (ХХ.6) и (ХХ.7) получим
J1/J2 = H - υT(dp/dT). (XX.8)
При переносе одного моля через перегородку переносится как его энтальпия H, так и Qраств. Знак "минус" определяется тем, что тепло выделяется в начале и поглощается в конце переноса. Таким образом:
J1/J2 = H - Qраств. (XX.9)
В результате из уравнений (ХХ.8) и (ХХ.9) получаем dp/dT = Qраств/υT, что согласуется с формулой (ХХ.4).
Согласно уравнению (ХХ.З), знак и величина переноса определяются теплотой растворения газа в перегородке. Если эта теплота равняется нулю, то переноса нет. Теплота растворения относится к общему понятию, играющему большую роль в термодинамике необратимых процессов, к так называемой "теплоте переноса". Так определяют тепло, переносимое при переходе одного моля (дополнительно к энтальпии самого этого моля). В рассмотренном переносе через перегородку моль растворяется по одну сторону перегородки (при этом выделяется теплота растворения), а затем этот моль выделяется по другую сторону перегородки (при этом поглощается теплота растворения). В результате происходит перенос количества тепла, равного теплоте растворения. Таким образом, эффект переноса при стационарных процессах зависит от пути переноса, в отличие от того, что имеет место при обратимых процессах. В случае, если теплота растворения в перегородке равна нулю, но в перегородке имеются весьма малые поры или капилляры, то при наличии градиента температуры возникает также перенос вещества, который носит название эффузии. Этот эффект возникает в том случае, когда диаметр путей в перегородке существенно меньше длины свободного пробега молекул. Поэтому такой эффект просто осуществляется при помощи вакуума. При движении вещества в описанной выше перегородке молекулы не сталкиваются друг с другом, а сталкиваются только со стенками капилляров. В результате молекула в перегородке не может непосредственно
538
осуществлять поступательное движение по капиллярам. Следовательно, она теряет одну поступательную степень свободы и отвечающую этой степени энергию RT/2 (в расчете на один моль). После выхода эта теплота вновь приобретается газом. Таким образом, теплота переноса при переходе через перегородку равна RT/2. Заменяя в уравнении (ХХ.3) Qраств на RT/2, получим:
|
d ln p |
|
dT |
=
|
RT |
|
2RT2 |
=
|
1 |
|
2T |
. (XX.10)
После интегрирования этого уравнения получим:
ln (p2/p1) = 1/2ln(T2/T1) или p2/p1 = √T2/T1.
Отсюда следует, что отношение давлений по обе стороны перегородки пропорционально корню квадратному из отношения температур.
Рассмотрим перенос через перегородку, пропускающую пар и не пропускающую жидкость. Такая перегородка может быть осуществлена из пористого несмачивающегося жидкостью материала. Пусть в жидкость погружена трубка, на дне которой находится перегородка. Тогда жидкость для перехода в трубку должна испаряться по одну сторону перегородки и сконденсироваться по ее другую сторону. Поэтому теплота переноса равняется теплоте испарения жидкости λ.
Если температура жидкости выше таковой в паре (трубке), то начнется перенос жидкости через перегородку, то есть осуществится своеобразный тепловой насос. Расчет показывает, что в случае воды при разнице температур в 100° C, процесс подъема прекратится, когда высота жидкости в трубке будет составлять несколько километров. Таким образом, этот тепловой насос способен поднимать жидкость на высоту, измеряемую в километрах. При термодиффузии градиент температуры вызывает перенос примеси. Величина такого переноса должна зависеть от механизма его осуществления. В простой теории Виртца, описывающей вакансионный механизм переноса, учитывается, что при совершении элементарного акта блуждания атом переходит от одной температуры к другой. При этом энергию, необходимую для преодоления активационного барьера, частица получает в начале блуждания и отдает в конце. Подобный переход возможен, если вакансия образуется в конце пути и исчезает в начале. В итоге тепло переноса должно составлять разницу энергий, равную высоте потенциального барьера и энергия образования вакансии.
