5. N-арное отношение. Область определения.

N-арное отношение – подмножество произведения нескольких множеств.

Множество первых элементов упорядоченных пар, входящих в отношение R, составляет его область определения

Отношение— математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.

n-местным (n-арным) отношением, заданным на множествах , называется подмножество прямого произведения этих множеств.

6. Бинарное отношение.

Бинарным отношением из множества А в множество В называется подмножество прямого произведения А и В.

Бинарным отношением на множестве М называется подмножество R декартова квадрата

М х М (т.е. подмножество множества всех упорядоченных пар элементов из М).

7. Рефлексивное бинарное отношение.

Пусть R подмножество A², тогда отношение R называется рефлексивным, если

aRa.

В математике бинарное отношение R на множестве Х называется рефлексивным, если всякий элемент этого множества находится в отношении R с самим собой.

Формально, отношение R рефлексивно, если :

Если это условие не выполнено ни для какого элемента множества Х, то отношение R называется антирефлексивным.

Формально антирефлексивность отношения R определяется как:

Если условие рефлексивности выполнено не для всех элементов множества Х, говорят, что отношениеR нерефлексивно.

Примеры рефлексивных отношений

• отношения эквивалентности:

  • отношение равенства 

  • отношение сравнимости по модулю

  • отношение параллельности прямых и плоскостей^{[источник не указан 104 дня]}

  • отношение подобия геометрических фигур;

• отношения нестрогого порядка:

  • отношение нестрогого неравенства 

  • отношение нестрогого подмножества 

  • отношение делимости 

[править]Примеры антирефлексивных отношений

• отношение неравенства 

• отношения строгого порядка:

  • отношение строгого неравенства 

  • отношение строгого подмножества 

• отношение перпендикулярности прямых (или ортогональности ненулевых векторов) в геометрии.

8. Арефлексивное бинарное отношение.

Бинарное отношение, не удовлетворяющее условям рефлексивности.

9. Симметричное бинарное отношение.

Примером симметричных отношений могут быть равенство (=),отношение эквивалентности, подобия, одновременности, некоторые отношения родства (например, отношение братства).

В математике бинарное отношение R на множестве X называется симметричным, если для каждой пары элементов множества a,b выполнение отношения aRb влечёт выполнение отношения bRa. Формально, отношение R симметрично, если

10. Антисимметричное бинарное отношение.

Двухместное отношение R, определённое на некотором множестве и отличающееся тем, что для любых х и у из xRy и xR⁻¹y следует х = у (то есть R и R⁻¹ выполняются одновременно лишь для равных между собой членов).

В математике бинарное отношение R на множестве X называется антисимметричным, если для каждой пары элементов множества a,b выполнение отношений aRb и bRa влечёт a = b. Формально, отношение R антисимметрично, если

11. Асимметричное бинарное отношение.

. Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Асимметричное отношение — бинарное отношение R, определённое на некотором множестве и отличающееся тем, что для любых х и у из xRy следует yRx. Пример: отношение «больше» (>) и «меньше» (<).

асимметричное это арефлексивное и антисимметричное отношение

12. Транзитивное бинарное отношение.

Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».

В математике бинарное отношение R на множестве X называется транзитивным, если для любых трёх элементов множества a,b,c выполнение отношений aRb и bRc влечёт выполнение отношения aRc. Формально, отношение R транзитивно, если

13. Понятие отношения порядка.

Антисимметричное транзитивное отношение называется отношением порядка. Если рефлексивное, то отношение нестрогого порядка. Если антирефлексивное, то – строгого порядка.

Бинарное отношение R на множестве X называется отношением порядка, если имеют место

• Транзитивность:

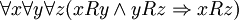
• Антисимметричность:

• Отношение порядка называется нестрогим, если оно

• Рефлексивно:

Напротив, отношение строгого порядка

• Антирефлексивно (или иррефлексивно)

Отношение порядка называется полным (линейным), если любые два элемента множества так или иначе связаны этим отношением, то есть:

Полнота:

Полностью (линейно) упорядоченное множество называют также цепью. Очевидно, полнота (линейность) отношения порядка влечет рефлексивность этого отношения, поэтому такой порядок всегда нестрогий.

Рефлексивное, транзитивное, антисимметричное отношение называется частичным порядком. А рефлексивное, транзитивное (но не обязательно антисимметричное!) отношение называется квазипорядком (или предпорядком).

Обычно отношение строгого порядка (полного или частичного) обозначается знаком <, а отношение нестрогого порядка — знаком