SuslovaNA-7
.docИСПОЛЬЗОВАНИЕ МНОГОФАЗНЫХ КОДОВ ДЛЯ СИНХРОНИЗАЦИИ СИГНАЛОВ И РАЗДЕЛЕНИЯ КАНАЛОВ СВЯЗИ
Н.А. Суслова, студент каф. РТС
Научный руководитель А.С. Бернгардт, доцент каф. РТС
Томск, ТУСУР, rioka@sibmail.com
Проект ГПО РТС-1206 – Разработка дидактического модуля для исследования технологии широкополосного беспроводного доступа
Для синхронизации и разделения каналов связи используются ансамбли сигналов с хорошими автокорреляционными свойствами и при этом слабо коррелированные между собой. Рассмотрим возможность использования для этих целей многофазных кодов, которые представляют собой многофазные последовательности с идеальной периодической автокорреляционной функцией (АКФ). Наибольшее распространение получили коды Задова-Чу (или квадратичных вычетов) и коды Фрэнка, которые базируются на аппроксимации закона линейной частотной модуляции.
Коды Фрэнка возможны
только для периодов кодовых
последовательностей, являющихся
квадратом некоторого числа
.
Элементы кода квадратного периода
определяются выражением
,
где
В отличии от кода
Фрэнка, коды Задова-Чу существуют для
любого периода
и определяются выражением
,
где
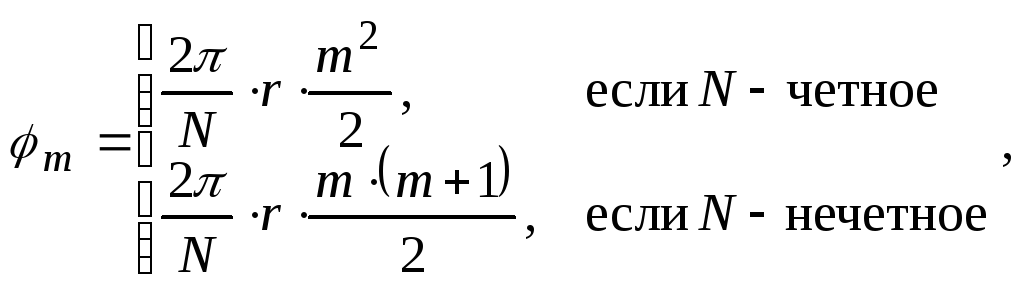
– целое число
взаимно простое с
Для периода
,
меняя
,
можно получать ансамбли слабо
коррелированных между собой сигналов.
Уровень боковых
лепестков в зависимости от периода
для обоих кодовых последовательностей
представлен на рис. 1.
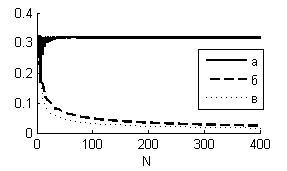
Рис. 1. Уровень
боковых лепестков импульсной АКФ в
зависимости от
(а, б – максимальный и минимальный уровни
боковых лепестков кода Задова-Чу, в –
уровень боковых лепестков кода Фрэнка)
По рис. 1 видно, что импульсная АКФ многофазных кодов имеет низкий уровень боковых лепестков, в следствие чего можно судить об их хороших автокорреляционных свойствах, причем у кода Фрэнка эти показатели лучше. Преимущества