
МЕТОДИЧКА ПО MAPLE и MATHCAD
.pdf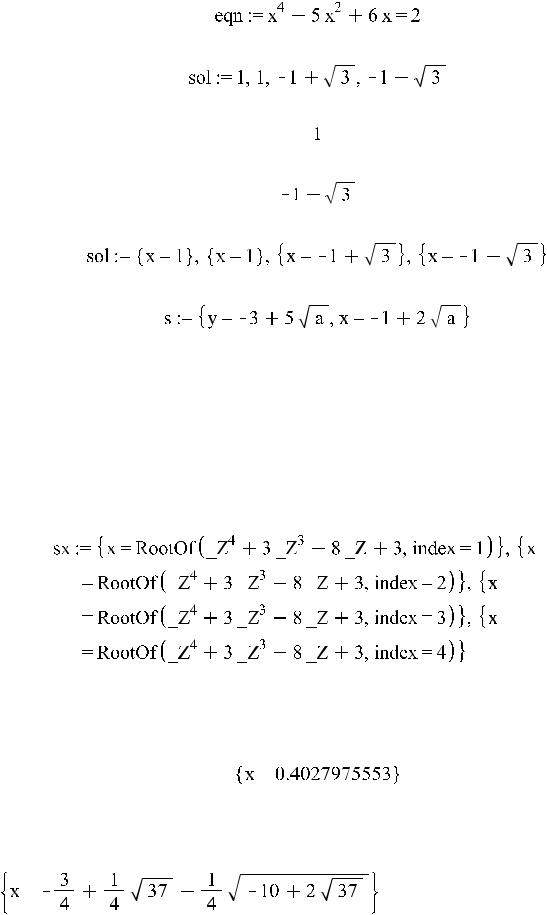
51
>sol:=solve(eqn,x);
>sol[2];
>sol[4];
>sol:=solve({eqn},x);
>s:=solve({3*x-y=sqrt(a),5*x-2*y=1},{x,y});
Поиск решения может потребовать больших ресурсов памяти и времени. Для нелинейных уравнений может быть найдено несколько решений (но не обязательно все), а может оказаться, что не найдено не одного решения. Если в ответе появляется функция RootOf, это означает, что Maple, либо не может выразить решение в радикалах, либо это требует дополнительных усилий.
> sx:=solve(x^4+3*x^3-8*x+3,{x});
Само решение при этом выражается через корни аргумента функции, стоящей внутри RootOf. Его можно найти численно
> evalf(sx[1]);
Функция allvalues позволяет представить решение, используя радикалы
> allvalues(sx[1]);
> allvalues({sx});
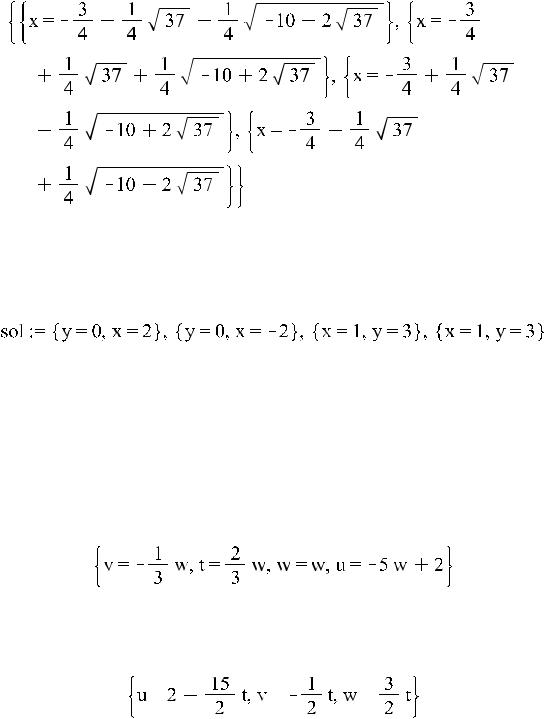
52
Решение системы уравнений
>eq:=(y+2*x)*y=5*y,x^2+y-4=0:
>sol:=solve({eq},{x,y});
Обратите внимание! Последние два решения совпадают, т.е. решения являются кратными.
Если неизвестных больше, чем уравнений, то Maple выберет какие, либо переменные в качестве параметров, например для системы, из трех уравнений с четырьмя переменными получим решение в виде
>eq:={w+u+4*v+8*t=2, v*3+w=0,v=3*w-5*t}:
>solve(eq);
Явное указание неизвестных позволяет получить решение с нужным параметром
> solve(eq,{u,v,w});
Численного решения системы уравнений функция fsolve()
Синтаксис функции fsolve(eqn,var,opt). С помощью дополнительного параметра opt могут быть заданы условия, устанавливающие местоположение, тип и число разыскиваемых решений.
Параметры команды fsolve
a..b или x=a..b Задание интервала [a,b] для поиска решений avoid={x=s} Поиск решений отличных от x=s
complex Поиск комплексных решений maxsols=n Поиск n наименьших решений

|
53 |
x=s |
Начальное приближение |
|
В качестве примера рассмотрим полином шестой степени, для |
которого найдем корни, применяя команду fsolve без параметров
>poly:=x^6-2*x^5-4*x^4-6*x^3+15*x^2+56*x-60:
>fsolve(poly);
Найдем два наименьших корня полинома
> fsolve(poly,x,maxsols=2);
Найдем вещественные и комплексные корни, отличающиеся от двух выше найденных
> fsolve(poly,x,complex,avoid={x=-2,x=1});
При решении трансцендентных уравнений желательно указывать предполагаемое положение корней. Решение без указания начального приближения (Трансцендентное уравнение ̵̵уравнение, не являющееся алгебраическим). Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции.
> fsolve(cos(Pi*x)=x);
Решение с указанием начального приближения в виде точки
> fsolve(cos(Pi*x)=x,x=0.5);
Задание начального приближения в виде интервала
> fsolve(cos(Pi*x)=x,x=-0.9..0.5);
Графическое решение уравнения
> plot([cos(Pi*x),x],x=-Pi..Pi);
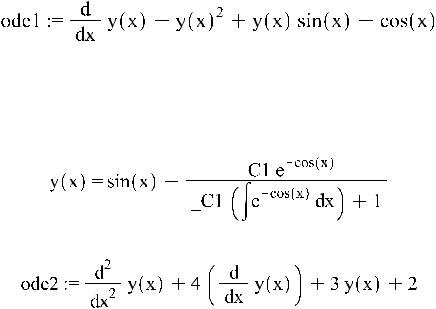
54
Функция solve позволяет находить решения одного неравенства относительно одной переменно. Кроме команд solve и fsolve в Maple имеются функции isolve(en) для отыскания решения уравнения в целых числах и msolve(eqn.m) для нахождения решения уравнения по модулю m.
Решение обыкновенных дифференциальных уравнений (ОДУ)
Для получения аналитических, приближенных и численных решений дифференциальных уравнений применяется функция dsolve, причем во всех случаях используется единый синтаксис команды: dsolve(ODE,var,opt), здесь ODE дифференциальное уравнение или система дифференциальных уравнений относительно неизвестной функции var. Для решения задачи Коши в уравнение ODE нужно включить так же начальные условия, а для краевой задачи соответственно краевые условия. Условие opt позволяют указать способ решения (type=.....) и используемый метод (method=....). В уравнениях для указания производно применяется команда diff и оператор D, а для обозначения производной в начальных и краевых условиях используется оператор D. Система уравнений оформляется в виде множества: уравнения, начальные и краевые условия помещаются в фигурные скобки и записываются через запятую.
Аналитические решения ОДУ
> ode1 := diff(y(x),x)-y(x)^2+y(x)*sin(x)-cos(x);
Решение уравнения без задания начальных, граничных условий и метода решений. Обратите внимание на то, что решение уравнения содержит неопределенную постоянную _C1
>dsolve(ode1);
>ode2:=diff(y(x),x,x)+4*diff(y(x),x)+3*y(x)+2;
Зададим начальные условия y'(0)=0, y(0)=-1. Обратите внимание, в этом случае решение уже не содержит неопределенную постоянную.

55
>ic:=D(y)(0)=0,y(0)=-1:
>dsolve({ode2,ic},y(x));
>ode3:=y(x)*diff(y(x),x,x)+diff(y(x),x)+1=0;
Зададим начальные условия y'(a)=0, y(0)=0
>ic:=y(0)=0,diff(y(a),a)=0:
>simplify(dsolve({ode3,ic},y(x)));
>ode4:=diff(y(x),x,x)= (y(x)*x+y(x)*ln(x)*x^2+diff(y(x),x)*ln(x)*x^2)/ln(x)/x^2*exp(x)- y(x)/ln(x)/x^2;
>dsolve(ode4);
>ode5:=diff(y(x),x)*x=x+2*y(x);
>dsolve(ode5);
56
Численное решение дифференциальных уравнений
>with(plots):
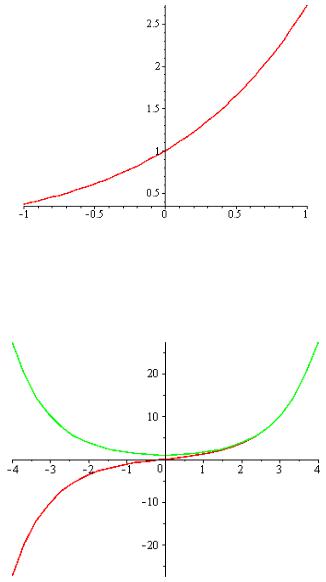
>p:= dsolve({D(y)(x) = y(x), y(0)=1}, y(x),type=numeric):
>odeplot(p,[x,y(x)],-1..1);
>sys := diff(y(x),x)=z(x),diff(z(x),x)=y(x): fcns := {y(x), z(x)}: p:= dsolve({sys,y(0)=0,z(0)=1},fcns,type=numeric):
>odeplot(p, [[x,y(x)],[x,z(x)]],-4..4,numpoints=25);
Функциональные операторы
Функциональные операторы являются альтернативой функций. Используются две формы записи оператора ̵стрелочная и с помощью угловых скобок. Например:
>x->x^2:
><x^2|x>:
означает подстановку x^2 на место x.
Рассмотрим пример работы с функциональным оператором
>F:=(x)->`if`(x=0,1,sin(x)/x):
>(F(0));
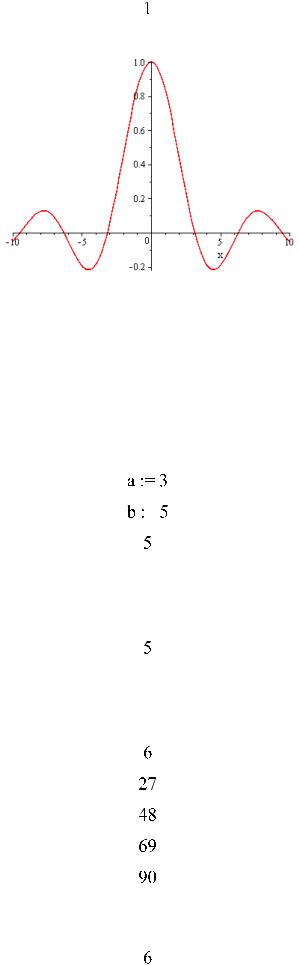
57
> plot(F(x),x=-10..10);
Условные операторы
Использованная выше форма записи оператора if аналогична форме используемой в MathCAD, однако Maple содержит конструкцию оператора if , близкую к конструкции оператора, используемой в языках С и Pascal
>a := 3; b := 5;
>if (a > b) then a else b end if;
или
>c:=3: d:=5:
>if (c > d) then c else d fi;
Операторы цикла. В Maple используются следующие операторов цик-
ла for, while - do
> for i from 6 by 21 to 100 do print(i) end do;
или
> for i from 6 by 21 to 100 do print(i) od;
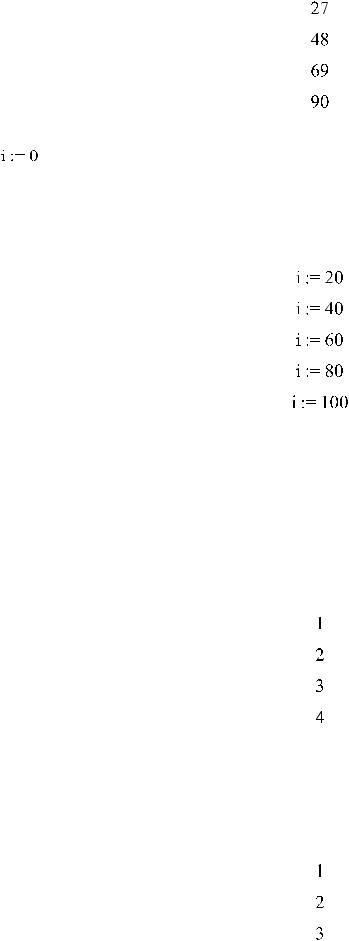
58
>restart; i:=0;
>while i<100 do i:=i+20
od;
Изменение естественного хода цикла с помощью операторов next и break например
> for i in[1,2,3,-2,4]do if i=-2 then next
else print(i) fi;
od;
> for i in[1,2,3,-2,4]do if i=-2 then break
else print(i) fi;
od;
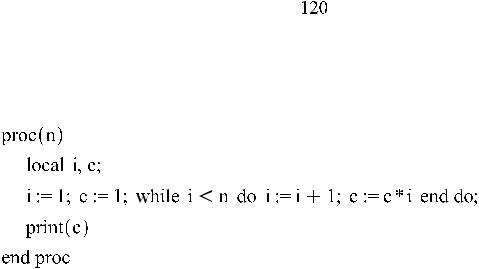
59
Процедуры
Форма задания процедуры имеет вид name:=proc(параметры) объявление процедуры;
local (список локальных переменных) объявление локальных переменных;
global (список глобальных переменных) объявление глобальных переменных;
options (список опций) объявление опций; Тело процедуры
end; (или end:)
>n_fact:=proc(n) local i,c;
i:=1;
c:=1; while i<n do i:=i+1; c:=c*i;
od;
print(c);
end:
>n_fact(5);
Текст процедуры можно вывести на печать с помощью команды print(имя процедуры)
> print(n_fact);
Последовательности, списки
Последовательность (sequence) это набор элементов разделенных запятыми, без скобок. Например
S:=1,2,3,4;
Для генерации последовательности в пакете Maple служит команда
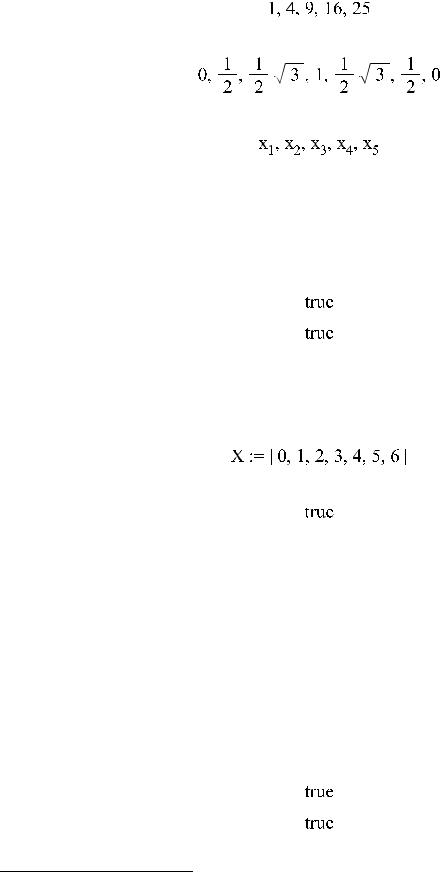
60
seq. Пример применения команды seq
>seq(i^2, i=1..5);
>seq(sin(Pi*i/6), i=0..6 );
>seq( x[i], i=1..5 );
Список(list) создается помещением через запятую элементов внутрь квадратных скобок
>A:=[a,sin(x),3,4]:
>B:=[[1,2,3],[2,4,3]]:
>type(A,list);type(B,list)2;
Создать список можно помещая команду seq в квадратные скобки. Пример
>X := [seq( i, i=0..6 )];
>type(X,'list');
Массивы (array), таблицы (table)
Для создания массива служит функция array. Синтаксис функции array
array(i..n,list1) формируется одномерный массив (вектор) с индексацией от i до n и элементами из списка list1,
array(i..n.j..m,list2) формируется массив (матрица) с элементами из списка list2.
>Va:=array(1..4,[a,sin(x),3,4]):
>Mb:=array(1..2,1..3,B):
>type(Va,array);type(Mb,array);type(Mb,matrix);
2 Функция type() проверяет тип переменной на соответствие ее типу list.
