МЕТОДИЧКА ПО MAPLE и MATHCAD

где x, y - действительные числа, A, D- комплексные числа, векторы или матрицы.

Вместе с функцией if можно использовать и более сложные условия, так выражение

(x<1) (x>0)

соответствует логическому «и», возвращающему 1, если х лежит внутри интервала (0,1), а выражение

(x>1)+(x<0)

логическому «или» возвращающему 1, если или х>1, или x<0.

Пример применения функции if i: 1..10

h: 0.1 p: 1 q: 2

f (x,u1,u2): if (u1 u2,sin(x),cos(x)) yi : f (i h, p,q)

zi : f (i h,q, p)

т.е. yi=cos(i h), zi=sin(i h).

Функция until

Функция until используется, чтобы управлять процессом итераций. Это единственная функция Mathcad, специально предназначенная для работы с дискретным аргументом, она позволяет останавливать вычисления, когда выполняется определенное условие.

Синтаксис функции until yi+1:=until(f(i), yi), где f(i) - условие,

проверяемое на i- той итерации, yi - результат вычислений на i - той итерации.

Вычисления прекращаются, как только f(i) станет меньше нуля. Пример применения функции until (извлечь корень из 3 с погрешностью

122

err:=10-12) n:=100 i:=0..n y0:=1 err:=10-12 a:=3

Итерационная процедура вычисление корня квадратного из числа а

Ступенчатые и импульсные функции

Ступенчатая функция Хэвисайда Ф(х) - возвращает 1, если х 0, иначе 0.

Символ Кронекера (i,j) - возвращает 1, если i=j, и 0, если i j. С помощью функций Хэвисайда и if можно создавать различные

импульсные функции, например: p(x,w):=Ф(x)- Ф(x-w),

функция p(x,w) - равна 1 на интервале 0 х w и 0 вне него. q(x,w):=if((x u) (x v),1,0),

функция q(x,w) -равна 1 на интервале u x v и 0 вне него.

торы, знаковые операторы.

126

Предопределенная переменная TOL задает точность решения уравнения (чем меньше TOL, тем точнее решение, однако, тем больше время решения).

Для нахождения корней уравнения, имеющего вид

n

y(x) ai xi 0, i 0

следует воспользоваться функцией polyroots, для которой не требуется задания начального приближения.

Для решения системы уравнений необходимо выполнить следующую последовательность операций:

задать нулевое приближение для всех неизвестных, входящих

всистему уравнений,

напечатать ключевое слово Given. Оно указывает Mathcad, что далее будет решаться система уравнений,

ввести ниже Given систему уравнений. Между левой и правой частями уравнений должен стоять знак = ( [Ctrl]=),

введите имя переменной, в которой будет содержаться решение системы уравнений (если вы решаете задачу с n неизвестными, то переменную следует задать, как вектор размерности n, войдя в меню

128

d y F(x, y), y(0)=y0 - начальное условие, dx

где F(x,y) известная функция своих аргументов. Выражение для функции D(x,y) в этом случае будет иметь вид

D(x,y)=F(x,y). В качестве примера рассмотрим текст программы решения уравнение Бернулли

аналитическое выражение для решения этого уравнения известно оно для данного значения y0=1 имеет вид

Текст программы численного решения уравнения приведен ниже: n:=100 число точек, в которых ищется решение уравнения a:=0 начальная точка интервала

b:=0.9 конечная точка интервала y0:=1 начальное условие

D(x,y):=x ((y0)2+3 y0) z:=rkfixed(y,a,b,n,D)

извлекаем из матрицы z столбец, содержащий решение уравнения задаем дискретный аргумент

h: (b a)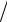n задаем шаг изменения аргумента x задаем дискретное значение точного решения уравнения vi : 3 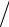4 exp 1.5 i h 2 1

относительная погрешность численного решения уравнения di : ui vi vi

График относительной погрешности численного решения

129

Решение системы дифференциальных уравнений первого порядка

Рассмотрим в качестве примера решение следующей системы уравнений

dx2 x1 exp( sin(t)), x2(0) 1 dt

или в матричном виде

Текст программы численного решения системы уравнений OLDORIGIN:=ORIGIN запоминаем старое значение ORIGIN ORIGIN:=1 устанавливаем новое значение

n:=100 число точек, в которых ищется решение уравнения. a:=0 начальная точка интервала

b:=2 конечная точка интервала

1

x: начальные условия

1

z:=rkfixed(x,a,b,n,D)

задаем дискретные значения точных решений системы уравнений

Ui: exp(sin((i 1) h)),

Vi: (i 1) h 1

относительные погрешности численного решения системы уравнений

ORIGIN:=OLDORIGIN восстанавливаем старое значение.

График относительных погрешностей численного решения

130

Решение дифференциальных уравнений порядка выше первого

Рассмотрим уравнение

Введя замену переменных d yi 1 yi , преобразуем исходное уравне- dt

ние в систему уравнений

Выражение для функции D(t,y) примет вид

В качестве примера рассмотрим решение уравнения

Текст программы

OLDORIGIN:=ORIGIN запоминаем старое значение ORIGIN ORIGIN:=1 устанавливаем новое значение n:=100 число точек, в которых ищется решение уравнения. a:=0 начальная точка интервала

b:=2 конечная точка интервала