Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metody_optimizatsii_Shatina_A_V

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 213 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

L( x,λ ) = λ	0	( x x				2	+ x		2	x		3	) + λ	(x2	+ x2	- 2) + λ			2	( x	2	+ x	3	- 2)	.
	0			1		2			2			3	1	1	2				2		2		3		.
Найдем стационарные точки из системы уравнений:
ì∂L( x,λ )								= λ0 x2 + 2λ1x1 = 0,
ï				¶x				= λ0 x2 + 2λ1x1 = 0,
ï					1
ï¶L( x,λ )								= λ ( x + x ) + 2λ x + λ = 0,
ï				¶x	2						0		1	3	1		2	2
ï											0		1	3	1		2	2
ï
ï¶L( x,λ )								= λ0 x2 + λ2 = 0,
í				¶x3				= λ0 x2 + λ2 = 0,
ï				¶x3
ïx			2 + x2					= 2,
ï		1					2
ïx			2	+ x			3	= 2,
ï			2				3
îïλ02 + λ12 + λ22 ¹ 0.

Если λ0 = 0, то из третьего уравнения получаем λ2 = 0. То-

гда из первого и второго уравнения получим x1 = 0, x2 = 0, что противоречит ограничениям задачи.

Положим λ0 = 1. Тогда из первых трех уравнений системы

= -λ

, x =

λ2

, x

= 2λ λ

- λ

λ2

получим:

2λ1

2λ1 . Подставим

эти значения x1, x2 , x3 в четвертое и пятое уравнения системы:

éì

= ±

4λ1

êïλ1

ì λ22

ìλ

êí

+ λ = 2

ïλ

= -1

- 4

-1

êî 2

4λ12

4 1

(

λ2 )

Û êìλ

4 1+ 4

ï 1

= 1±

= 2

2λ λ - 2λ

= 2

1 2

2λ

ï(

λ2

- 4

êí

1± 3

1 -1

êï

êïλ2

2 .

ëî

Получаем следующие стационарные точки:

P1( −1;1;1)

при

λ =

, λ

= -1

;

P2 (1;1;1)

при

= -

, λ

= -1

;

-1

+ 5

3 +1

;

= 1+

3 ç

;

ø при

-1

5 -

1- 3

;

= 1-

4 ç

2 .

ø при

Для исследования полученных стационарных точек восполь-

зуемся условиями второго порядка:

(

λ )

L x,

hi h j

= 2λ1h12 + 2λ1h22 + 2h1h2 + 2h2h3

¶x

;

i, j

(

′(

ˆ)

) =

(

′

( ˆ)

)

h3 .

2x1h1

2x2h2 ;

Для точки P1 имеем:

(

′(

ˆ)

)

= −

2h1

2h2

(

′(

ˆ)

) =

h2,h3

= −

;

( ˆ

λ )

L x,

hi h j = h12

+ h22 + 2h1h2

+ 2h2h3 = 2h22 > 0 "h2 ¹ 0

¶x

i, j 1

Согласно достаточным условиям второго порядка P1 locmin з .

Для точки P2 имеем:

(

′(

ˆ)

)

2h1

2h2

(

′

( ˆ)

, h

)

= −

, h3

= −

h2 ;

( ˆ

λ )

L x,

hi h j

= -h12

- h22 + 2h1h2

+ 2h2h3 = -6h22 < 0 "h2 ¹ 0

¶x

i, j 1

Следовательно, P2 locmax з . Для точки P3 имеем:

(f1¢( xˆ), h) = (3 -1)h1 - (3 +1)h2 = 0; ( f2¢( xˆ), h) = h2 + h3 = 0 Û

Ûh1 = (2 + 3)h2 ,h3 = -h2 ;

							23
3		¶	2	( ˆ	λ )
3			2	( ˆ	λ )
å				L x,		hihj	= (2 + 3)h12 + (2 + 3)h22 + 2h1h2 + 2h2h3 =
å			¶x ¶x			hihj	= (2 + 3)h12 + (2 + 3)h22 + 2h1h2 + 2h2h3 =
=			¶x ¶x		j
i, j	1			i	j

= (30 +183)h22 > 0 "h2 ¹ 0. Следовательно, P3 locmin з .

Для точки P4 имеем:

(f1¢( xˆ),h) = -(3 +1)h1 + (3 -1)h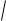2 = 0; ( f2¢( xˆ),h) = h2 + h3 = 0 Û

Ûh1 = (2 - 3)h2 ,h3 = -h2

( ˆ

λ )

L x,

hihj

= (2 - 3)h12

+ (2 - 3)h22 + 2h1h2 + 2h2h3 =

¶x ¶x

i, j

= (30 -18

)h2

< 0 "h ¹ 0

Следовательно, P4 locmax з .

Уравнения связи задают эллипс в трехмерном пространстве, который получается в пересечении цилиндра и плоскости. Это означает, что экстремум функции ищется на замкнутом ограниченном множестве. По теореме Вейерштрасса существует решение задачи на абсолютный минимум и абсолютный максимум.

Вычислим значение целевой функции в полученных точках:
f	0	( P ) = 0, f				0	( P ) = 2, f					0	( P ) = - 5 + 3 3										, f	0	( P ) = 3 3 - 5
	0	1				0	2					0		3						2				0		4				2 .
																				2										2 .
Сравнивая между собой полученные значения, делаем вы-
вод, что P3 absmin з , P2 absmax з .
Ответ:											æ																	ö
																+1					-1		5 -
P ( -1;1;1) Î locmin з; P															3	+1				3	-1		5 -				3
											ç	-							;			;				÷			Î locmax з
											ç	-							;			;				÷			Î locmax з
1								4			ç			2						2				2		÷				;
			æ								è			2				ö		2				2		ø				;
					-1					+1		5 +																		5 + 3
				3	-1				3	+1		5 +					3													5 + 3	3
		P	ç				; -				;							÷	Î absmin з, S							min			= -
		P	ç				; -				;							÷	Î absmin з, S										= -
		3	ç	2				2						2				÷												2		;
			è	2				2						2				ø												2		;
								P2 (1;1;1) absmax з, Smax = 2.																								●

Задачи для самостоятельного решения.

2.1.5 − 3x1 − 4x2 → extr; x12 + x22 = 25.

2.2.x1x22 → extr; x1 + 2x2 −1 = 0.

2.3.e2x1x2 → extr; x1 + 2x2 = 3.

2.4.x1 + x2 → extr; 5x12 + 4x1x2 + x22 = 1.

2.5.1− 4x1 − 6x2 → extr; 4x12 + 4x1x2 − 7x22 = 32.

2.6.x1 + x2 + x3 → extr; x1 + x2 − x3 = 1, x12 + x22 + x32 = 1.

2.7.x12 + x22 + x32 → extr; x1 + x2 + x3 = 1.

2.8.x1x22 x33 → extr; x1 + x2 + x3 = 1.

2.9.1− 4x1 − 8x2 → extr; x12 − 8x22 = 8.

2.10.2x12 +12x1x2 + x22 → extr; x12 + 4x22 = 25.

2.11.x14 + x24 → extr; ( x1 −1)3 − x22 = 0.

2.12. x1x2 x3 → extr; x1 + x2 + x3 = 4, x1x2 + x2 x3 + x3 x1 = 5.

2.13.	x2	+ x2		→ extr; ( x			−1) 2 + x2					= 4			.
	1		2			1				2
	x	+ x		+ x		→ extr;		1	+	4	+		9	= 1

2.14.	1		2		3			x1		x2			x3 .

2.15.2x12 + 3x22 + 4x32 → extr; x1 + x2 + x3 = 13.

2.16.(a, x) → extr; ( x, x) = 1, a, x Rn .

2.17.	Найти	расстояние от	точки ξ Rn		до гиперплоскости
(a, x) = b, a Rn , b R
		.		ξ Rn
2.18.	Найти	расстояние	от точки			до прямой

x = at + b, a,b Rn , t R .

Занятие 3. Гладкие конечномерные экстремальные задачи с ограничениями типа равенств и неравенств.

Постановка задачи:

Пусть xˆ = ( xˆ1,..., xˆn )

f0 ( x) ® min;

f1( x) £ 0,..., fr ( x) £ 0,

fr+1( x) = 0, fm ( x)

= 0,

(1)

где функции n переменных fk ( x) : Rn → R (k = 0,1,..., m)

опреде-

лены и непрерывно дифференцируемы в

некоторой

области

U Rn .

Определение. Множество

X = { x ÎU : f1( x) £ 0,..., fr ( x) £ 0, fr+1( x) = 0,

fm ( x)

= 0}

называется множеством допустимых точек задачи (1).

▲

Определение. Говорят, что допустимая точка x доставляет в

задаче (1) локальный минимум, и пишут x

locmin з , если

δ >

такое, что для любой допустимой точки

x , удовлетворяющей

−

< δ

(

)

(

)

³ f0

условию

, выполнено

неравенство

x .

▲

В задачах, имеющих ограничение в виде неравенств, важно, является ли рассматриваемая задача задачей на минимум или задачей на максимум. Задачу на максимум можно свести к задаче на минимум:

f0 ( x) ® max, x Î X Û - f0 ( x) ® min, x Î X .

		m
Определение.	Функция	L( x,λ ) = åλk fk ( x)	,	где
		k=0

λ = (λ0 ,λ1,...,λm ) , называется функцией Лагранжа задачи (1), а

числа λ0 ,λ1,...,λm - множителями Лагранжа. ▲ Теорема. (Необходимые условия локального минимума 1-го

порядка)

- точка локального минимума в задаче

(1), а функции f0 ( x), f1( x),..., fm ( x) непрерывно дифференцируемы в некоторой окрестности этой точки. Тогда существует нену-

левой вектор множителей Лагранжа λ = (λ0 ,λ1,...,λm ) такой, что выполняются условия:

а) стационарности функции Лагранжа:

	( ˆ	λ )			m
	¶L x,		= 0, i = 1,2,...,n	Û	å	λ	¢( ˆ)	= 0
						λ	¢( ˆ)
	¶xi						k fk x
	¶xi				k=0			;
б) дополняющей нежесткости:

λ	j f j	(	ˆ)		= 0,	j = 1,...,r ;
			x
в) неотрицательности:				³ 0,		j = 0,1,...,r .
	λ j						■

Следует отметить, что условия дополняющей нежесткости выписываются для ограничений, задаваемых в виде неравенств, а

условия неотрицательности					- для множителей Лагранжа, соот-
ветствующих целевой функции							f0 ( x) и ограничениям, задавае-
мым в виде неравенств.									ˆ
									ˆ
Определение. Допустимые точки x , в которых выполняются
условия а), б), в), называются критическими.											▲
Для решения задач вида (1) с ограничениями типа равенств
и неравенств следует:										m
										m
									L( x,λ ) = åλk fk ( x)
1) Составить функцию Лагранжа										k=0	.
2) Найти критические точки из системы уравнений и нера-
венств:
ì∂L( x,λ )						= 0, i = 1,..., n,
ï			¶x		i	= 0, i = 1,..., n,
ï			¶x
ï
ïλ j			f j ( x) = 0,						j = 1,..., r,
ï				³ 0, j = 0,1,..., r,
íλ j				³ 0, j = 0,1,..., r,
ï f	j		( x) £ 0,				j = 1,..., r,
ï	j
ï f j ( x) = 0,							j = r +1,..., m,
ï				,λ ,...,			λ		) ¹ 0.
ï(λ		0		,λ ,...,			λ	m	) ¹ 0.		(2)
î		0			1			m			(2)
При этом следует рассмотреть							отдельно два			случая:	λ0 = 0 и

λ0 ¹ 0. В случае λ0 ¹ 0 положить λ0 равным единице или другой положительной константе.

3) Провести исследование полученных решений системы

(2).

Замечание. Если требуется найти все экстремумы функции, то следует сначала решить задачу на минимум, а затем решить задачу на максимум, сведя ее к задаче на минимум.

Пример 1.

x12 + 4x22 + x32 ® min; 2x1 - 2x2 - x3 £ 6, x1 + 2x2 - x3 = 3.

Решение. Составим функцию Лагранжа

L( x,λ ) = λ0 (x12 + 4x22 + x32 )+ λ1(2x1 - 2x2 - x3 - 6) +

				+ λ2 ( x1 + 2x2 − x3 − 3)
Найдем критические точки из системы уравнений и нера-
венств:
ì∂L( x, λ )					= 2λ0 x1 + 2λ1 + λ2 = 0,
ï		¶x			= 2λ0 x1 + 2λ1 + λ2 = 0,
ï				1
ï	¶L( x, λ )				= 8λ x - 2λ + 2λ = 0,
ï	¶x			2			0		2		1		2
ï							0		2		1		2
ï
ï	¶L( x, λ )				= 2λ x - λ - λ = 0,
ï	¶x						0		3	1		2
í				3			0		3	1		2
í				3
ïλ (			2x1 - 2x2 - x3 -							6	)	= 0,
ï	1		2x1 - 2x2 - x3 -							6		= 0,
ïλ0 ³ 0, λ1 ³ 0,
ï2x - 2x					2	- x		3	£ 6,
ï		1			2			3
ïx1 + 2x2 - x3 = 3,
ïλ2			+ λ2		+ λ2			¹ 0.
î	0			1		2

1) Если λ0 = 0, то из первых трех уравнений системы полу-

чим λ1 = 0, λ2 = 0 , что противоречит последнему неравенству системы.

2) Положим λ0 = 1. Получим следующую систему для нахождения критических точек:

ì2x1 + 2λ1 + λ2 = 0,

ï4x

- λ + λ

= 0,

ï2x3 - λ1 - λ2 = 0,

ïλ (2x - 2x

- x

- 6) = 0,

ï2x

- 2x

- x

£ 6,

ïx

+ 2x

- x

= 3,

îλ1 ³ 0.

(3)

Рассмотрим два варианта выполнения условия дополняю-

щей нежесткости (четвертого уравнения в системе (3)):

2.1)

λ1 = 0. Тогда

из

первых

трех уравнений получим

x1 = -λ2

x2 = -λ2

4 ,

x3 = λ2

2 . Подставляя эти значения

переменных

x1, x2 , x3 в шестое уравнение системы (3), получим

λ2 = -2 , следовательно,

x1 = 1, x2 = 1 2, x3 = -1. Таким образом,

получена

критическая

точка

P(1; 1 2;-1)

при

λ0 = 1, λ1 = 0,λ2 = -2.

Непосредственная проверка показывает,

что выполняются все уравнения и неравенства системы (3).

2.2) λ1 ¹ 0, 2x1 - 2x2 - x3 - 6 = 0. Тогда получим следующую

систему уравнений:

ì2x1 + 2λ1 + λ2 = 0,

ï4x

- λ + λ

= 0,

ï2x3 - λ1 - λ2 = 0,

í2x - 2x

- x

- 6 = 0,

ïx

+ 2x

- x

= 3,

ïλ

> 0.

выразим x1 , x2 , x3

Из первых трех уравнений системы

через

λ1,λ2 :

x = -	2λ1 + λ2 , x	2	= λ1 − λ2 , x	3	= λ1 + λ2
1	2		4		2 .

Подставив эти значения в четвертое и пятое уравнения си-
стемы, получим	λ1 = −12 7, λ2 = − 6 7 . Найденное значение λ1

противоречит условию λ1 > 0. Заметим, что множество

X = {( x1, x2 , x3 ) :2x1 − 2x2 − x3 ≤ 6, x1 + 2x2 − x3 = 3}

не является ограниченным. Кроме того, для целевой функции

справедливо неравенство

( x) = x2

+ 4x2

+ x2

³ x2

+ x2

3 .

lim f

0 ( x)

= +∞

Откуда следует, что

→∞

. Согласно следствию теоре-

мы Вейерштрасса существует решение задачи на абсолютный минимум. В силу единственности критической точки решением может быть только она.

Ответ: (1;12;−1) absmin з, Smin = 3, Smax = +∞ . ●

Пример 2.

x12 + 2x1 - 8x2 - 2x3 ® min; 9 - 3x1 - 3x2 - x3 £ 0, x2 £ 0,

4x1 + 3x2 + x3 = 40.

Решение. Составим функцию Лагранжа

L( x,λ ) = λ0 (x12 + 2x1 - 8x2 - 2x3 ) + λ1( 9 - 3x1 - 3x2 - x3 ) + λ2 x2 +

+ λ3 (4x1 + 3x2 + x3 − 40) .

Найдем критические точки из системы уравнений и неравенств:

ì¶L( x,λ )

= 2λ0 x1

+ 2λ0 - 3λ1 + 4λ3 = 0,

¶x

¶L( x,λ )

= -8λ0 - 3λ1 + λ2 + 3λ3 = 0,

¶x2

¶L( x,λ )

= -2λ0

- λ1 + λ3 = 0,

¶x3

ïλ (9 - 3x - 3x

- x

) = 0, λ

= 0,

¹ 0,

ïλ0 ,λ1,λ2 ³ 0, λ0

+ λ1

+ λ2 + λ3

4x1 + 3x2 + x3 = 40.

(4)

î9 - 3x1 - 3x2 - x3 £ 0, x2 £ 0,

1) Если λ0 = 0, то из первых трех уравнений системы полу-

чим λ1 = 0, λ2 = 0 , λ3 = 0 , т.е. все множители Лагранжа обращаются в ноль.

2) Положим λ0 = 1. Рассмотрим четыре варианта выполнения условий дополняющей нежесткости).

2.1) λ1 = 0, λ2 = 0 . Подставляя эти значения λ1, λ2 и λ0 = 1 в первые три уравнения системы (4), получим несовместную систему уравнений:

ì2x1 + 2 + 4λ3 = 0,

ïí- 8 + 3λ3 = 0, ïî- 2 + λ3 = 0.

2.2) λ1 = 0, λ2 ¹ 0. Тогда

<<< < Предыдущая 1 23 / 213 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015553.47 Кб11metodichka_Arkh_EVM_k_rabota_2011g.doc
#
12.11.2019702.98 Кб7Metodichka_Dogovornoe_pravo.doc
#
10.05.2015697.34 Кб19Metodichka_Dogovornoe_pravo.doc
#
10.05.2015237.39 Кб16Metodika_Po_Oech_Diplomov.pdf
#
10.05.201561.44 Кб11Metodologia_portalov (2).doc
#
10.05.20151.01 Mб41Metody_optimizatsii_Shatina_A_V.pdf
#
10.05.20153.97 Mб14metod_ACM.doc
#
19.11.201993.7 Кб7Metod_ukaz2.doc
#
01.07.2025209.6 Кб1Metrology_lec05.docx
#
01.07.202580.95 Кб0Metrology_lec1-2 (1).docx
#
01.07.202547.11 Кб0Metrology_lec4.docx