Metody_optimizatsii_Shatina_A_V

æ

− 72 − 36

ö

D = -72

< 0, D

= 2592 > 0 Þ

A(3;6) = ç

÷,

2

ç

- 36 - 54

÷

1

è

ø

Þ P1(3;6) Îlocmax f .

В точке P2 (0;12) :

A(0;12)

æ− 288 −144

ö

D = -288 < 0, D

= 0 -1442 < 0 Þ

= ç

÷,

2

ç

0

÷

1

è -144

ø

Þ P2 (0;12) Ïlocextr f .

Для точек

P3 (t;0), t Î (- ¥;+ ¥) :

A(t;0)

æ

0

0

ö

D

= 0, D

= 0 Þ

= ç

2

÷,

1

2

ç

0 24t -

2t

÷

требуется дополни-

è

ø

тельное исследование.

Рассмотрим точки P3 (t + ε1; ε 2 )

из окрестности токи P3 (t;0) .

f (t + ε

1

; ε

2

) - f (t;0) = (t + ε

1

)ε 2 (12 - t - ε

1

- ε

2

)

.

2

Если t < 0, то t + ε1 < 0, ε 22 ³ 0, 12 - t - ε1 - ε 2 > 0, следова-

тельно, f (t + ε1; ε 2 ) - f (t;0)

£ 0 и P3 (t;0) Î locmax f .

Если t

=

0 , то

f (ε

1

; ε

2

) - f (0;0) = ε ε 2 (12 - ε

1

- ε

2

)

. Так как

1

2

ε 22 ³ 0, 12 - ε1 - ε 2 > 0, а ε1

может быть как отрицательным, так

и положительным, то и P3 (0;0) Ï locextr f .

Если 0 < t < 12,

то

t + ε1 > 0, ε 22 ³ 0, 12 - t - ε1 - ε 2 > 0, сле-

довательно,

f (t + ε1; ε 2 )

- f (t;0) ³ 0 и P3 (t;0) Î locmin f .

Если t = 12, то

f (12 + ε

1

; ε

2

) - f (12;0) = (12 + ε

1

)ε 2 (- ε

1

- ε

2

)

.

2

Постановка задачи:

f0 ( x) ® extr; f1( x) = 0,..., fm ( x) = 0,

(1)

где функции n переменных fk ( x) : Rn → R (k = 0,1,..., m)

опреде-

лены и непрерывно дифференцируемы в некоторой

области

∂fk ( x)

, k = 0,1,...,m,

U Rn (т.е. fk ( x)

и ∂xi

i = 1,..., n определены и

непрерывны в U ).

Точки

x U , удовлетворяющие условиям

Определение.

в задаче (1).

ˆ

▲

Определение. Говорят, что допустимая точка x доставляет в

задаче (1)

локальный

минимум

(локальный

максимум):

ˆ

locmin з

ˆ

δ >

0 такое, что для любой до-

x

( x Î locmax з), если

−

ˆ

< δ

пустимой точки x , удовлетворяющей условию

x

x

, выпол-

нено неравенство f0

(

x

)

³ f0

( ˆ) (

f0

(

x

)

£ f0

( ˆ))

.

▲

x

x

m

fk ( x)

Определение.

Функция

L( x,λ ) = åλk

,

где

k=0

14

телей Лагранжа λ = (λ0 ,λ1,...,λm )

такой, что для функции Лагран-

жа задачи (1) выполняется условие стационарности по x :

(

ˆ

λ )

m

¶L x,

= 0, i

= 1,2,...,n Û å

λ

¢( ˆ)

= 0

¶xi

k fk

x

(2)

λ0 ¹ 0,

k=0

.

2)

Для

того,

чтобы

достаточно,

чтобы

векторы

′(

ˆ)

,...,

′

(

ˆ)

были линейно независимы.

■

f1 x

fm

x

Определение. Допустимые точки

ˆ

x , в которых выполнены

условия (2), называются стационарными.

▲

Теорема 2. (Необходимые условия локального экстремума

I-II порядка)

ˆ

(

ˆ

)

;

Пусть 1) x Î locmin з

x Î locmax з

2)

fk

(

x

)

Î D

2

(

ˆ)

,

k

= 0,1,...,m ;

x

3) система векторов

′(

ˆ)

′

( ˆ)

линейно независи-

f1

x

,..., fm

x

ма (условие регулярности).

Тогда

существует

вектор

множителей

Лагранжа

λ = (1,λ1,...,λm )

такой,

что

для

функции

Лагранжа

задачи

L( x,λ ) =

m

f0 ( x) + åλk fk ( x)

выполнены условия:

k=1

∂

( ˆ

λ )

L

x,

= 0, i = 1,2,..., n

¶xi

а) стационарности:

;

б)

неотрицательной

(неположительной)

определенности

квадратичной формы

æ n

2 (

λ )

ö

n

¶

2 (

ˆ

λ )

¶

ˆ

L x,

ç

L x,

÷

å=

hi h j ³ 0

å=

hi h j £

0

¶x

i

¶x

j

ç

¶x

¶x

j

÷

для

всех

i, j 1

èi, j

1

i

ø

h =

(

h1,...,hn

)

,

удовлетворяющих

условию

(

′

( ˆ)

, h

)

= 0 Û

fk

x

n

¶fk

(

ˆ)

hi

= 0, k = 1,..., m

Û å

x

=

¶x

.

■

i

1

i

Пусть 1)

fk

(

x

)

Î D

2

(

ˆ)

, k

= 0,1,...,m ;

x

2) система векторов

′(

ˆ)

′ (

ˆ)

линейно независи-

f1

x

,..., fm

x

ма (условие регулярности);

λ = (1,λ1,...,λm )

3) существует вектор множителей Лагранжа

такой,

что

для

функции

Лагранжа

задачи

m

L( x,λ ) = f0 ( x) + åλk fk ( x)

выполнены условия:

k=1

∂

( ˆ

λ )

L x,

= 0, i = 1,2,..., n

¶xi

а) стационарности:

;

б) положительной (отрицательной) определенности квадра-

тичной формы

λ )

æ n

2 (

λ )

ö

n

2 (

ˆ

ˆ

¶

å=

L x,

ç

¶ L x,

÷

¶x

i

¶x

j

hi h j > 0

ç å=

¶x

¶x

j

hi h j <

0 ÷

для

всех

i, j

1

èi, j

1

i

ø

h = (h1,...,hn ) ¹ 0

и

удовлетворяющих

условию

(

¢

( ˆ)

)

n

¶fk

( ˆ)

,h

= 0 Û å

x

hi

= 0, k = 1,...,m

fk

x

¶x

=

i

. Тогда

i

1

ˆ

ˆ

(

)

.

■

x Î locmin з

x Î locmax з

Здесь запись

fk

(

x

)

Î D

2

(

ˆ)

,

k = 0,1,...,m означает, что функции fk

x

n

переменных

определены

в

некоторой

окрестности

точки

ˆ

( ˆ

ˆ

)

и

имеют

непрерывные

частные производные до

x =

x1,..., xn

m

1)

Составить функцию Лагранжа

L( x,λ ) = åλk fk ( x)

.

k=0

2)

Найти стационарные точки из системы уравнений

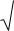
ì¶L( x,λ )

= 0, i = 1,..., n,

ï

¶x

íï fk ( xi) = 0, k = 1,..., m,

ï(λ

0

,λ ,...,λ

m

) ¹ 0.

ï

1

ï

(3)

î

Следует отдельно рассмотреть случаи λ0 = 0

и λ0 ¹ 0. Если

λ0 ¹ 0, то, умножив все множители Лагранжа λk

на одно и то же

мер, линейной независимости векторов

′(

ˆ)

′

( ˆ)

. Следую-

f1

x

,..., fm

x

щий пример показывает, что не всегда можно полагать λ0 = 1.

Пример 1.

f

0

( x , x

2

) = x ® min;

f

1

( x , x

2

) = x3 - x2

= 0

.

1

1

1

1

2

Из ограничения задачи получаем, что

x

= 3

x2

³ 0

, следова-

1

2

тельно, точка (0;0)

является решением. Однако, если сразу поло-

жить λ0 = 1, то функция Лагранжа примет вид:

L( x,λ ) = x + λ

(x3

- x2 )

.

1 1

1

2

Система уравнений для нахождения стационарных точек

выглядит следующим образом:

ì¶L( x,λ )

= 1+ 3λ x2 = 0,

ï

¶x

1

1

ï

1

ï

¶L( x,λ )

= -2λ1x2

= 0,

í

¶x2

ï

ïx3

- x2

= 0.

ï

1

2

î

Если же

L( x,λ ) = λ

x + λ

(x

3 - x2 )

, то система (3) принима-

0 1

1

1

2

ет вид:

ì¶L( x,λ )

= λ

+ 3λ x2 = 0,

ï

¶x

0

1

1

ï

1

ï

¶L( x,λ )

= -2λ1x2 = 0,

ï

¶x2

í

ï

3

2

ï

= 0,

ïx1

- x2

ïλ2

+ λ2

¹ 0.

î

0

1

Откуда получаем λ0 = 0, λ1 = t,

t Î R, t ¹ 0, x1 = 0, x2 = 0

.

●

Пример 2.

x

+ 2x

2

® extr;

x2

+ x2

= 5

.

1

1

2

Решение.

Составим

функцию

Лагранжа

L( x,λ ) = λ

0

( x + 2x

2

) + λ

(x2 + x2

- 5)

.

1

1

1

2

18

ì¶L( x,λ )

= λ0 + 2λ1x1 = 0,

ï

¶x

ï

1

ï

¶L( x,λ )

= 2λ0 + 2λ1x2 = 0,

ï

¶x2

í

ï

2

2

ï

= 5,

ïx1

+ x2

ïλ2

+ λ2

¹ 0.

î

0

1

нию связи.

2) Положим λ0 = 1. Тогда

ì1+ 2λ x

= 0,

ï

1

1

+ 2λ1x2

= 0, Û

í2

ïx

2 + x2

= 5.

î 1

2

é λ

= 1 2,

ì