Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metody_optimizatsii_Shatina_A_V

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2113 14 15 16 17 18 19 20 21 > Следующая >>>

121

1	2		2		n
B( xn ) = ò (n	2	- n(t -1))dt = n	2	+	n	® +¥
B( xn ) = ò (n		- n(t -1))dt = n		+	2	® +¥
0						при n → ∞.

Для последовательности функций ~xn (t) = n

(- n)dt -

B( xn ) = ò

= -n - 2 ® -¥

при n → ∞.

t2 + 3

Ïlocextr з, Smax = +¥, Smin = -¥

Ответ:

x(t) = -

. ●

Пример 3.

π 2

- 4x cost)dt + x

B( x) =

- 4x

π ö

® extr

ò (x

2 ø

Решение: Выпишем интегрант задачи и терминант задачи:

	2			l = x	2	æπ		ö
	2	- 4x	2	l = x		ç	2	÷
L(t, x, x) = x		- 4x		- 4x cost ,		è	2	ø.

Необходимые условия локального экстремума: а) уравнение Эйлера

-dtd Lx + Lx = 0 Û - dtd (2x) - 8x - 4cost = 0 Û x + 4x = -2cost ; б) условия трансверсальности

Lx (0) = lx(0) 2x(0) = 0 x(0) = 0,

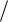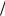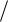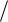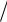Lx (π2) = −lx(π2) 2x(π2) = −2x(π2) x(π 2) = −x(π 2) .

Общее решение дифференциального уравнения Эйлера складывается из общего решения соответствующего однородного

уравнения	x + 4x = 0	и частного	решения неоднородного:
x = xoo + xч .
Общее	решение	однородного	уравнения имеет вид:

xoo = C1 sin 2t + C2 cos 2t . Частное решение неоднородного уравнения следует искать в виде: xч = Acost + B sin t .

Значения постоянных A, B находятся непосредственной подстановкой функции xч в дифференциальное уравнение. Получаем:

122

A = 6, B = 0. Тогда

x(t) = C1 sin 2t + C2 cos 2t + 6cost,

x(t) = 2C1 cos 2t - 2C2 sin 2t - 6sin t .

Постоянные C1,C2 найдем из условий трансверсальности:

x(0) = 0 Þ 2C1 = 0,

x(π 2) = -x(π 2) Þ - 2C1 - 6 = C2 .

Тогда

C1 = 0, C2 = -6,

= 6(cost - cos 2t) .

x(t)

Проведем исследование полученного решения. Для этого

возьмем

произвольную

допустимую

функцию

+ h(t), h(t) ÎC

([0;π 2])

и рассмотрим разность

x(t) = x(t)

π 2 é

B(x + h) - B(x) =

- 4(

+ h)

- 4(

= ò

ê(x + h)

+ h) costúdt + (x(π 2) + h(π 2)) -

π 2

(π 2) =

ò (x

4x cost)dt - x

π 2

(

(π 2) =

2xh

+ h

− 8xh −

− 4h cost)dt + 2x(π 2)h(π 2) + h

π 2

- 4hcost)dt +

π 2

- ò

= 2xh

2xhdt + ò

- 8xh - 4h

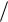+2xˆ(π2)h(π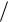2) + h2 (π 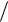2) =

=πò2 (- 2xˆ - 8xˆ - 4cost)hdt + πò2 (h2 - 4h2 )dt +

+(2xˆ(π2) + 2xˆ(π2))h(π 2) - 2xˆ(0)h(0) + h2 (π 2) .

Сучетом того, что функция xˆ(t) удовлетворяет уравнению Эйлера и условиям трансверсальности, получим:

π 2

- 4h

]dt + h

(π 2)

"h(×) ÎC

([0;

π 2])

B(x + h) - B(x) = ò

Покажем, что xˆ(t) Ïlocextr з . Для этого рассмотрим две последовательности функций, сходящихся к тождественно нулевой

123

функции по норме пространства C1([0;π2]) . Действительно, для

последовательности функций

(t)

n получим:

π 2

1- 2π

= ò

ê-

údt

< 0

B(x

+ hn ) - B(x)

(t) = sin 4t

А для последовательности функций

π 2 é16cos2 4t

4sin2 4t ù

3π

> 0

B(x + hn )- B(

= ò

údt =

Следовательно, x(t) locextr з .

Покажем, что Smax = +∞, Smin = −∞. Действительно, для по-

следовательности функций xn (t)

= n имеем:

B( xn )

= πò2 (- 4n2 - 4n cost)dt + n2 = (1- 2π )n2 - 4n ® -¥

при n → ∞.

Для последовательности функций xn (t) = nsin 4t

π 2

ò (16n

cos

4t - 4n

sin

4t - 4nsin 4t cost)dt =

B( xn ) =

3πn2 - 16n ® +¥

= 15 при n → ∞.

Ответ: xˆ(t) = 6(cost − cos 2t) locextr з, Smax = +∞, Smin = −∞ .●

Пример 4.

B( x) = πò (x2 + x2 - 4x sin t)dt + 2x2 (0) + 2x(π ) - x2 (π ) ® extr

Решение: Интегрант и терминант задачи имеют вид:

L = x2 + x2 - 4x sin t, l = 2x2 (0) + 2x(π ) - x2 (π ) . Выпишем необходимые условия локального экстремума:

124

а) уравнение Эйлера

- dtd Lx + Lx = 0 Û - dtd (2x) + 2x - 4sin t = 0 Û x - x = 2sin t ; б) условия трансверсальности

Lx (0) = lx(0) Û 2x(0) = 4x(0) Û x(0) = 2x(0) ,

Lx (π ) = -lx(π ) Û 2x(π ) = -2 + 2x(π ) Û x(π ) = x(π ) -1.

Общее решение уравнения Эйлера имеет вид: x(t) = C1cht + C2 sht + sin t .

Продифференцируем полученную функцию по t : x(t) = C1sht + C2cht + cost .

Постоянные C1,C2 найдем из условий трансверсальности: x(0) = 2x(0) Þ C2 +1 = 2C1 ;

x(π ) = x(π ) -1Þ C1shπ + C2chπ -1 = C1chπ + C2shπ -1. Решая систему линейных уравнений второго порядка относитель-

но C1,C2 , получим:

x(t)

= sht + cht + sin t = et

= 1, C

= 1,

+ sin t

Исследуем полученное решение. Для этого возьмем произ-

вольную допустимую функцию x(t)

+ h(t),

h(t)

ÎC

([0;

π ]) и

= x(t)

рассмотрим разность

+ (

B(x + h)

- B(x) = ò

ê(x

+ h)

x + h) - 4(x

+ h)sin túdt + 2(x(0) + h(0)) +

+ h(π ))

ˆ2

+ 2(x(π ) + h(π )) - (x(π )

- ò

+ x

4x sin t]dt -

- 2x

(π ) =

(0) - 2x(π ) + x

ˆ2

+ h

- 4hsin t]dt

= ò[2xh + h

+ 2xh

(0) + 2h(π ) - 2x(π )h(π ) - h

(π ) =

= +4x(0)h(0) + 2h

125

- 4hsin t]dt +

+ ò

+ h

= 2xh

[- 2xh + h

+ 2xh

(

0) + 2h(π ) - 2x(π )h(π ) - h

(π ) =

+ 4x(0)h(0) + 2h

- 2x(π ))h(π ) + (-

= (2x(π ) + 2

2x(0) + 4x(0))h(0) +

+ h

]dt + 2h

(0)

- h

(π ) =

+ ò

[- 2x + 2x

- 4sin t]hdt + ò

+ h

]dt + 2h

(

0) - h

(π )

= ò

= h

(π ) - h

(0)

ò 2hhdt = h

Заметим, что 0

. Поэтому

]dt

+ h

(0)

- h]

+ h

(0) ³ 0

B(x + h)

- B(x)

= ò

- 2hh + h

= ò

Следовательно,

= e

+ sin t Î abs min з .

x(t)

+ sin t Î abs min з .

Ответ: x(t) = e

●

Пример 5.

1	x		2	dt + 4e	x(0)	+ 32e	−x(1)	® extr
B( x) = ò e		× x		dt + 4e		+ 32e		® extr
0								.

Решение: Выпишем интегрант задачи и терминант задачи:

L = L( x, x) = ex x2 , l = 4ex(0) + 32e−x(1) .

Необходимые условия локального экстремума: а) уравнение Эйлера

- dtd Lx + Lx = 0 Û - dtd (2xex )+ ex x2 = 0 ; б) условия трансверсальности

Lx (0) = lx(0) Û 2x(0)ex(0) = 4ex(0) Û x(0) = 2,

Lx (1) = -lx(1) Û 2x(1)ex(1) = 32e−x(1) Û x(1) = 16e−2x(1) .

126

Так как интегрант не зависит явно от t , то уравнение Эйлера имеет интеграл энергии:

xLx - L = const Û x × 2xex - ex x2 = const Û ex x2 = const .

Тогда

xex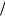2 = C1, ex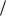2dx = C1dt, 2ex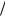2 = C1t + C2,

x =

2ln

C1t + C2

2C1

C t + C

2 .

Из условий трансверсальности найдем постоянные C1, C2 :

2C1

= 2 Û C1 = C2 ;

x(0)

2 Þ

2x 1

−

( )

Þ C + C

= 16ç C + C

x(1) = 16e

ø .

Откуда получаем следующие значения для C1, C2 : C1 =C2 = 2 .

Единственная

допустимая

экстремаль

имеет

вид:

x(t) = 2ln(t +1) .

Проведем исследование полученного решения. Для этого

возьмем

произвольную

допустимую

функцию

([0;1])

и рассмотрим разность

x(t) = x(t) + h(t), h(t) ÎC

x+h

x(0)+h(0)

−x(1)−h(1)

B(x + h) - B(x)

(x + 2xh + h )dt +

+ 32e

= òe

1 ˆ

x(0)

−x(1)

= ò[e

-1)

x+h

]dt

- òe

× x

dt - 4e

- 32e

× x

2xhe

+ e

+4exˆ(0)+h(0) + 32e−xˆ(1)−h(1) - 4exˆ(0) - 32e−xˆ(1) .

Сучетом уравнения Эйлера проинтегрируем по частям первое слагаемое, стоящее под знаком интеграла и учтем условия трансверсальности:

1	ˆ		2		h	1	d		ˆ	h
	x		2		h		d		x	h
		ˆ		(e				ˆ		)×(e -1)dt =
		ˆ						ˆ
òe × x						-1)dt = ò dt (2xe
0						0

127

= (2xe )× (e -1)

- ò(2xe

)× e hdt =

h(1)

h(0)

−x(1)

x(0)

= 32e

-1)- 4e

-1)- ò (2xe

)×e hdt

Тогда

x+h 2

B(x + h) - B(x) =

x(0)

−x(1)

x(0)+h(0)

−x(1)−h(1)

h dt

+ 4e

+ 32e

- 4e

32e

= òe

32e−x(1) (eh(1) -1)

- 4ex(0) (eh(0) -1) =

x+h 2

−x(1)

2ch(h(1))

−x(1)

h dt

+ 32e

- 32× 2e

= òe

1 ˆ

+16(ch(h(1)) -1) ³ 0

òe

+ h(×)

вы-

Так как для любой допустимой функции x(×) = x(×)

³ 0, то найденная экстремаль

полнено неравенство B(x + h) - B(x)

x(t) = 2ln(t +1) доставляет в задаче абсолютный минимум.

= 2ln(t +1) Î abs min з .

●

Ответ: x(t)

Задачи для самостоятельного решения.

+ x

)dt - 2x(1)sh1 ® extr

ò (x

9.1.0

- 6xt)dt + x

(1) - 4x(0) ® extr

ò (x

9.2. 0

)dt

- x

(0) + 6x(1)

® extr

ò (12xt - x

9.3. 0

+ x(12t

8))dt + x

(0) + 4x(2)

® extr

ò (x

9.4.0

																		128
	π 2					2		- x		2	)dt		+ x	2		(	0) - x			2		æπ			ö		æ	π ö	® extr
		ò				2				2				2						2		æπ			ö		æ	π ö
		ò			(x																	ç		2	÷	+ 4 xç		÷
9.5.		0																				è		2	ø		è	2 ø	.
9.5.		0																											.
	π 2					2		- x		2	- 2x)dt - 2x							2	(0)					- x		2æ	π ö	® extr
		ò				2				2								2								2æ	π ö
		ò			(x																					ç	÷
9.6.		0																								è	2 ø		.
9.6.	2	0																											.
	2		2		2		dt		-	2x(1) + x					2		(2) ® extr
9.7.	òt				x		dt		-	2x(1) + x							(2) ® extr
9.7.	1																								.
	e					2									2		(1) - x				2		(e) - 4x(e) ® extr
	ò					2									2						2
9.8.	ò	2(tx						+ xx)dt + 3x
9.8.	1												)dt + 2x(1)( x(0)																.
	1			t+1			2		+ 2x			2													+1)		® extr
	òe					(x			+ 2x																+1)		® extr
9.9. 0		e−1																											.
		e−1								2	dt + 2x(0)( x(e -1) +1) ® extr
										2
9.10.			ò(t +1)x																										.
9.10.			0																										.

9.11. Найти допустимые экстремали функционала Больца

3	2 2		4
B( x) = ò 4x	2 2	dt + x	4	(0) -8x(3)
B( x) = ò 4x	x	dt + x		(0) -8x(3)
0				.

Занятие 10. Изопериметрическая задача.

Определение. Изоперимтерической задачей классического вариационного исчисления называется следующая экстремальная

задача в пространстве C1([t0 ;t1]) :

I0 ( x(×))	=	t1
		ò
			f0 (t, x(t), x(t))dt ® extr;
t1		t0			(з)

Ii ( x(×)) = ò				i = 1,..., m
	fi (t, x(t), x(t))dt = αi ,
t0	x(t0 ) = x0 , x(t1 ) = x1.			,	(1)
					(2)

129

Здесь α1,...,αm - заданные числа, отрезок [t0 ;t1] фиксирован и конечен, t0 < t1. Ограничения (1) называются изопериметриче-

скими. Функции x(×) ÎC1([t0 ;t1]) , удовлетворяющие условиям (1), (2), называются допустимыми.

Определение. Говорят, что допустимая функция xˆ(×) доставляет слабый локальный минимум (максимум) в задаче (з), пишут:

	ˆ		ˆ		δ > 0 такое, что для любой до-
	x Îlocmin з (x Îlocmax з) , если				δ > 0 такое, что для любой до-
пустимой			функции	x(×) ,	удовлетворяющей		условию
	ˆ
	ˆ
	x(×) - x(×)	1	< δ , выполнено неравенство
	x(×) - x(×)	1	< δ , выполнено неравенство
				ˆ	(I0 ( x(×)) £ I0	ˆ	▲
			I0 ( x(×)) ³ I0 (x(×))		(I0 ( x(×)) £ I0	(x(×))) .	▲
					m

				L(t, x, x) = åλi		fi (t, x, x)	называется
	Определение. Функция				i=0		называется

лагранжианом задачи, а числа λ0 ,λ1,...,λm - множителями Ла-

гранжа.

▲

доставляет слабый локальный

Теорема. Пусть функция x(×)

экстремум в поставленной задаче (з) (x(×) Îlocextr з) , а функции

fi , fix , fix

(i = 0,1,...,m)

непрерывны как функции трех перемен-

ˆ ˆ

ных в

некоторой

окрестности

множества {(t, x(t), x(t))

t Î[t0;t1]}.

Тогда

существует

ненулевой

вектор

множителей

Лагранжа

λ = (λ

,λ ,...,λ

) Î Rm+1

такой, что для функции Лагранжа задачи

([t

;t ])

L выполнено условие

L (t) ÎC

и справедливо уравнение

Эйлера:

;t ]

L (t)

+ L

(t) = 0 "t Î

■

Рассмотрим примеры решения изопериметрических задач.

Пример 1.

			130
1	2	dt ® extr;	I1( x(×))	1	x(0) =1, x(1) = 6
I0 ( x(×)) = ò x		dt ® extr;	I1( x(×))	= ò xdt = 3,	x(0) =1, x(1) = 6
0				0	.

Решение: Составим Лагранжиан задачи: L = λ0x2 + λ1x . Выпишем необходимое условие экстремума – уравнение Эйлера:

- dtd Lx + Lx = 0 Û - dtd (2λ0x) + λ1 = 0 Û -2λ0x + λ1 = 0 .

Если λ0 = 0, то из уравнения Эйлера получим, что λ1 = 0, следовательно, вектор множителей Лагранжа получается нулевым.

Поэтому λ0 ¹ 0. Положим λ0 = 12. Тогда

														λ t	2
			x = λ , x = λ t + C ,									x =		1			+ C t + C				2
			x = λ , x = λ t + C ,									x =					+ C t + C
						1	1	1				2							1			.
												2										.
	Неизвестные постоянные λ1, C1,C2 найдем из граничных
условий и изопериметрического условия:
						x(0) = 1 Þ C2 = 1,
						x(1) = 6 Þ			λ1		+ C + C					2		= 6
						x(1) = 6 Þ					+ C + C							= 6
								2				1								,
								2												,				1
1	xdt = 3 Þ		1	æ	λ t	2		ö				= 3 Û			λ t3					C t2	+ C		t		= 3 Û


ò			ò	ç	1	+ C t + C		÷dt								1			+	1
ò			ò	ç	2	1		2 ÷								6				2		2
0			0	è			λ1	ø		C1														0
0			0	è				ø																0
						Û		+					+ C2 = 3
						Û		+					+ C2 = 3					.
							6	2										.
Откуда		получаем: λ1 = 6, C1 = 2, C2 = 1. Единственная																							допусти-
													ˆ		3t			2	+ 2t +1.
мая экстремаль задачи имеет вид: x(t) =															3t				+ 2t +1.

Покажем с помощью непосредственной проверки, что xˆ(t) доставляет абсолютный минимум в задаче, т.е. покажем, что для

любой допустимой	функции	x	выполнено				неравенство
ˆ	функцию	h(	×) ÎC	1	([t0	;t1])	такую, чтобы
I0 ( x) ³ I0 (x) . Возьмем

функция x(t) = xˆ(t) + h(t) была допустимой. Из ограничений задачи получим условия, которым должна удовлетворять функция h :

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2113 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015553.47 Кб8metodichka_Arkh_EVM_k_rabota_2011g.doc
#
12.11.2019702.98 Кб4Metodichka_Dogovornoe_pravo.doc
#
10.05.2015697.34 Кб14Metodichka_Dogovornoe_pravo.doc
#
10.05.2015237.39 Кб12Metodika_Po_Oech_Diplomov.pdf
#
10.05.201561.44 Кб5Metodologia_portalov (2).doc
#
10.05.20151.01 Mб31Metody_optimizatsii_Shatina_A_V.pdf
#
10.05.20153.97 Mб9metod_ACM.doc
#
19.11.201993.7 Кб3Metod_ukaz2.doc
#
10.05.2015687.76 Кб17MIREA_Ekonomika_Metodichka_1076_2011.pdf
#
10.05.2015479.74 Кб25MIR_Kursovoy_proekt_Morina_A_I_ISB-3-12.doc
#
10.05.20153.2 Mб88mukrrtc2ssss011.doc