Metody_optimizatsii_Shatina_A_V

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

+ 2x)dt → extr;

≤ 1, x(0) = 3

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2118 19 20 21 > Следующая >>>

171

m	m	, x(t0 ),t1, x(t1))
f (t, x,u) = å	λi fi (t, x,u) ,l(t0, x(t0 ),t1, x(t1)) = åλiψ i (t0	, x(t0 ),t1, x(t1))
i=0	i=0	,

выполнены условия:

а) стационарности по x – уравнение Эйлера для лагранжиа-

на


L = f (t, x,u) + p(t)( x -ϕ(t, x,u)) :
	d	ˆ		ˆ
−		L		(t) + L	x	(t) = 0	t	T
−	dt	L		(t) + L		(t) = 0	t	T	;
	dt		x						;
б) трансверсальности по x для терминанта
		m
l = åλiψ i (t0, x(t0 ),t1, x(t1))
		i=0						:

Lˆx (tˆ0 ) = lˆx(t0 ) Lˆx (tˆ1) = −lˆx(t1 )

в) оптимальности по u :

min L(t, xˆ(t), xˆ(t) ,u(t))=

u U

min[ f (t, xˆ(t),u) − p(t)ϕ(t,

u U

г) стационарности по t0 ,

отрезка интегрирования):		(tˆ0
ˆ	ˆ
Λt0	= 0 − f

p(tˆ0 ) = lˆx(t0 ) ,

p(tˆ1) = −lˆx(t1 ) ;

			t T
L(t, x(t), x(t) ,u(t))			t T
	ˆ ˆ	ˆ
	ˆ	(t) − p(t)ϕ(t) t T		;
x(t),u)] = f		(t) − p(t)ϕ(t) t T		;
ˆ			ˆ

t1 (только для подвижных концов

) + lˆt0 + lˆx(t0 ) xˆ(tˆ0 ) = 0,

ˆ	ˆ ˆ	ˆ	ˆ			ˆ
Λt	= 0 f (t1) + lt				ˆ
Λt	= 0 f (t1) + lt		+ lx(t ) x(t1) = 0				;
1		1		1			;
д) дополняющей нежесткости:
	λi Bi (ξ ) = 0,	i = 1,...,l ;
е) неотрицательности: λi ³ 0, i = 0,1,...,l .							■

Пример 1. Решить экстремальную задачу:

min[ ](λ0u2 − pu) = λ0uˆ2 − puˆ

u −1;1

Решение: Приведем					задачу к виду			задачи оптимального

управления. Для этого введем управление u = x . Сначала решим
задачу на минимум, а затем – на максимум.
4
ò (u	2	+ 2x)dt → min;				u		= u
	2
							≤ 1, x(0) = 3, x
I. 0								.
Составим функцию Лагранжа задачи:
		4
		Λ = ò[λ0 (u	2
		Λ = ò[λ0 (u		+ 2x)+ p( x − u)]dt + λ1( x(0) − 3)
		0						.

Выпишем необходимые условия локального минимума: а) уравнение Эйлера для лагранжиана

L= λ0 (u2 + 2x)+ p( x − u)

−dtd Lx + Lx = 0 − dtd p + 2λ0 = 0;

б) условия трансверсальности для терминанта l = λ1( x(0) - 3)

Lx (0) = lx(0) Û p(0) = λ1, Lx (4) = -lx(4) Û p(4) = 0;

в) условие оптимальности по u :

;

Слагаемые в лагранжиане, не содержащие управление u , здесь опущены, так как они выступают в роли аддитивных посто-

янных и uˆ от них не зависит.

г) условие неотрицательности:

λ0 ³ 0.

Если λ0 = 0, то из уравнения Эйлера следует, что p = const , тогда из условия трансверсальности получим p(t) º 0, λ1 = 0, т.е. все множители Лагранжа обращаются в ноль. Поэтому λ0 ¹ 0.

173

Положим λ0 = 1. Тогда из уравнения Эйлера получим: p = 2, p = 2t + C1.

Так как p(4) = 0 , то p(t) = 2t − 8 и − 8 ≤ p(t) ≤ 0 на отрезке [0;4]. Условие оптимальности принимает вид:

min

- pu)

= u

- pu

u [−1;1]

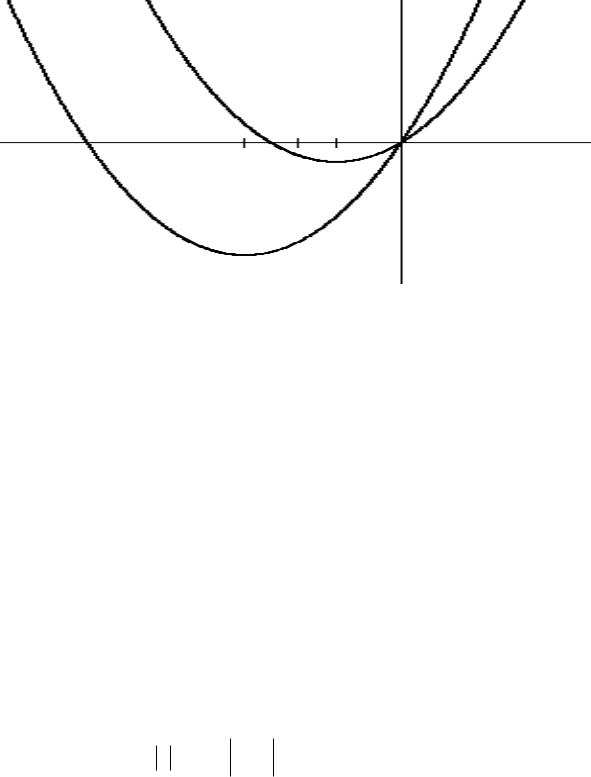
Графиком функции

ϕ(u) = u2

- pu

является парабола, ветви кото-

p2 ö

4 ÷

рой направлены вверх, а вершина имеет координаты è

(рис. 13.1). Поэтому

, если

³ -1,

t - 4,

если t - 4 ³ -1,

ï 2

= í

Û x

ï-1, если

£ -1.

î-1, если t - 4 £ -1.

С учетом того, что t [0;4], получаем:

	t - 4, если 3 £ t £ 4,				ì(t - 4)2		+ C1, если 3 £ t £ 4,
	ì			ˆ	ï
ˆ			Þ			2
x = í		£ t £ 3.		x = í
	î-1, если 0				ï		, если 0 £ t £ 3.
					î- t + C2

174

Рис. 13.1

Так как x(0) = 3, то C2 = 3. Из условия непрерывности

функции xˆ в точке t = 3 найдем константу C1:

12 + C1 = -3 + C2 Þ C1 = - 12 .

В итоге получаем единственно возможную экстремаль

ì3 − t, если 0 ≤ t ≤ 3, xˆ = ï

íït2 - 8t +15 , если 3 £ t £ 4.

î 2 Покажем с помощью непосредственной проверки, что

найденная функции xˆ(t) доставляет абсолютный минимум в задаче. Возьмем допустимую функцию x(t) = xˆ(t) + h(t) . Из условий

задачи получим ограничения для функции h(t) :

x(0) = 0 Û xˆ(0) + h(0) = 0Þ h(0) = 0 ;

x £ 1Þ xˆ + h £ 1 Û -1 £ xˆ + h £ 1. Оценим разность B(xˆ + h) - B(xˆ):

ˆ	1	é	2	ˆ	ù	4		2	ˆ
ˆ	ˆ	ˆ		ˆ			ˆ		ˆ
B(x + h) - B(x) = ò		ê(x + h)		+ 2(x + h)údt - ò			[x		+ 2x]dt =
	0	ë			û	0

175

4			2			4		4				4		2
4			2			4		4				4		2
	ˆ				ˆ		+ ò		ˆ
= ò (2xh + h				+ 2h)dt = 2xh		0	+ ò		(- 2x	+ 2)hdt + ò h dt =
0	3			4	4	0		0	3	4		0
0								0				0
							2	dt			2	dt
	= ò 2hdt + ò0× hdt + ò h							dt	= 2ò hdt + ò h			dt
	0			3	0				0	0			.

При t Î[0;3] справедливо двойное неравенство 0 £ h £ 2. Так
как h(0) = 0	и	h(t) не			убывает				на	отрезке				[0;3], то
							ˆ			ˆ			ˆ
h(t) ³ 0 "t Î[0;3]. Следовательно, B(x + h) - B(x) ³ 0											и x Îabsmin з

II. Приступим к решению задачи на максимум, сведя предварительно ее к задаче на минимум:

4
ò (- u	2	- 2x)dt ® min;			u	£1, x(0) = 3,
	2
								x = u
0								.
Функция Лагранжа имеет вид:
4
L = ò[- λ0 (u			2				( x(0) - 3)
L = ò[- λ0 (u				+ 2x)+ p( x - u)]dt + λ1			( x(0) - 3)
0								.

Выпишем необходимые условия локального минимума: а) уравнение Эйлера для лагранжиана

L = -λ0 (u2 + 2x)+ p( x - u) :

- dtd p - 2λ0 = 0 ;

б) условия трансверсальности для терминанта

l = λ1( x(0) - 3) : p(0) = λ1, p(4) = 0,

в) условие оптимальности по u :

min	(- λ0u	2	ˆ	2	ˆ
min	(- λ0u		- pu) = -λ0u		- pu
u [−1;1]					;

г) условие неотрицательности:

λ0 ³ 0.

Аналогично пункту I можно показать, что λ0 ¹ 0. Положим

x £ 1Þ 1+ h £ 1 Û -2 £ h £ 0 . Оценим разность B(xˆ + h) - B(xˆ):

ния. Рассмотрим допустимую функцию ничений задачи получим:

x(0) = 0 Þ h(0) = 0,

176

λ0 = 1. Тогда из уравнения Эйлера получим: p = -2, p = -2t + C1 .

Так как p(4) = 0 , то p(t)

= -2t + 8 и 0 £ p(t) £ 8 при t Î[0;4].

Условие оптимальности принимает вид:

min

(- u

ˆ2

- pu) = -u

- pu

u [−1;1]

Графиком функции

ϕ(u) = -u

2 - pu

является парабола, ветви ко-

p2 ö

;

4 ÷

торой направлены вниз, а вершина имеет координаты è

(рис. 13.2). Поэтому u =

1 Û x = 1Þ x = t + D1.

Так как x(0) = 3, то

x(t) = t + 3.

Выполним непосредственную проверку полученного реше- x(×) = xˆ(×) + h(×) . Из огра-

B(x + h) - B(
	ˆ
4		2
	ˆ		+
= ò (2xh + h			+
0

1	é		2		ˆ	ù	4		2	ˆ
ˆ	ˆ			+	ˆ			ˆ		ˆ
x) = ò	ê(x	+ h)		+	2(x + h)údt - ò			[x		+ 2x]dt =
0	ë					û	0
	4					4

2h)dt = ò (2 + h)hdt + 2ò hdt
	0					0 .

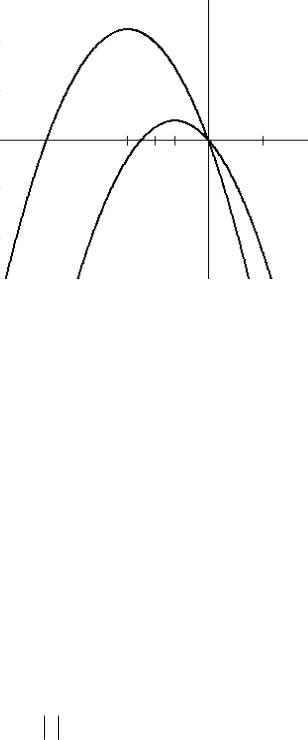
177

Рис. 13.2
									h(0) = 0 и h не
Так как - 2 £ h £ 0, то (2 + h)h £ 0 . А так как									h(0) = 0 и h не
							£ 0, то h(t) £ 0 на от-
убывает на отрезке [0;4] в силу условия h							£ 0, то h(t) £ 0 на от-
						4
резке	[0;4],			следовательно,		òhdt £ 0	.	Таким образом,
резке	[0;4],			следовательно,		0	.	Таким образом,
ˆ		ˆ		£ 0 и	ˆ
B(x + h) - B(x)				£ 0 и	x Îabsmax з.
Ответ:
	3 − t, если 0 ≤ t ≤ 3,
	ì
ˆ	ï	2				Îabsmin з		,	Smin =	35
x = í		2	- 8t +15 , если 3 £ t £			Îabsmin з		,	Smin =	3
	ït		- 8t +15 , если 3 £ t £			4.				3
	î			2						;
				ˆ	= t + 3Îabsmax з , Smax = 30.					●
				x(t)	= t + 3Îabsmax з , Smax = 30.					●

Пример 2. Решить экстремальную задачу:

ò xdt ® min; x £ 2, x(0) + x(4) = 0, x(0) = 0, x(4) = 0

0	.
Решение: Сведем поставленную задачу к задаче оптималь-
ного управления. Для этого вместо функции x(×)	введем век-

тор-функцию ( x1(×), x2 (×) ) и управление u , где x1 = x, x2 = x , u = x Тогда получим задачу:

178

ò x1dt ® min; u £ 2, x1(0) + x1(4) = 0, x2 (0) = 0, x2 (4) = 0,

x1 - x2 = 0, x2 - u = 0 . Составим функцию Лагранжа задачи:

L = 4ò[λ0x1 + p1( x1 - x2 ) + p2 ( x2 - u)]dt + λ1( x1(0) + x1(4)) + 0

+ λ2x2 (0) + λ3x2 (4).

Выпишем необходимые условия локального экстремума: а) система уравнений Эйлера для лагранжиана

L= λ0x1 + p1( x1 - x2 ) + p2 ( x2 - u) :

-dtd Lx1 + Lx1 = 0 Û - dtd p1 + λ0 = 0 ,

-dtd Lx2 + Lx2 = 0 Û - dtd p2 - p1 = 0; б) условия трансверсальности для терминанта

l = λ1( x1(0) + x1(4)) + λ2 x2 (0) + λ3 x2 (4) :

(0) = l

(0)

Û p (0) = λ

(4) = -l

( 4)

Û p (4) = -λ

(0) = l

(0)

Û p

(0) = λ

2 ,

(4) = -l

(4)

Û p

(4) = -λ

3 ;

в) условие оптимальности:

ì2, p2 > 0,

min

< 0,

[- p2u] = - p2u

Þ u

= í- 2, p2

u [−2;2]

ï[- 2;2],

= 0.

г) условие неотрицательности: λ0 ³ 0.

Если λ0 = 0, то из а) следует, что p1(t) º const , а так как p1(0) + p1(4) = 0, то p1(t) º 0. Тогда из второго уравнения Эйлера получим p2 (t) = C . Если C = 0 , то из б) следует, что

179

λ1 = λ2 = λ3 = 0, т.е. все множители Лагранжа равны нулю. Если

ˆ		ˆ
ˆ	ˆ	ˆ	. В этом случае приходим к
C > 0 , то u	= 2 Û x2 = 2 Þ x2 = 2t + C1		. В этом случае приходим к
			ˆ			ˆ
противоречию с краевыми условиями x2 (0) = 0, x2 (4) = 0. Если
ˆ		ˆ
ˆ	ˆ	ˆ	+ C1. Снова не выполняют-
C < 0 , то u	= -2 Û x2	= -2 Þ x2 = -2t	+ C1. Снова не выполняют-
		ˆ	. Поэтому	λ	0	¹ 0	.
ся краевые условия для функции x2 (t)			. Поэтому		0		.
			~
Положим λ0 = 1. Тогда p1 = 1, p = t + C . Так как

p1(0) + p1(4) = 0, то p1(t) = t - 2. Тогда из второго уравнения Эйлера

p2 = 2 - t, p2 (t) = - (t -22)2 + C .

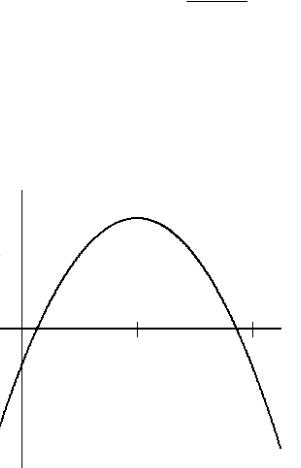
Графиком функции p2 (t) является парабола, ветви которой направлены вниз, а осью симметрии является прямая t = 2 . При

этом функция p2 (t) на отрезке [0;4] обязательно должна поменять знак (рис. 13.3), в противном случае придем к противоречию

с краевыми условиями для функции xˆ2 (t) .

Рис. 13.3 Из условия оптимальности получим:

180

ì- 2, t Î[0;τ ],

ì− 2t + C1, t [0;τ ],

= í 2, t Î[τ ;4 -τ ], Þ

= í 2t + C2, t Î[τ ;4 -τ ],

= x2

ï- 2, t Î[4 -τ ;4].

ï- 2t + C , t Î[4 -τ ;4].

Найдем неизвестные величины C1,C2 ,C3,τ из краевых усло-

и условия непрерывности в точках t = τ и

вий для функции x2 (t)

t = 4 −τ :

(0) = 0 Þ C1

= 0,

(4) = 0 Þ C3

= 8,

t = τ Þ -2τ = 2τ + C2 ,

t = 4 -τ Þ 2(4 -τ ) + C2 = -2(4 -τ ) + 8.

Откуда находим C1 = 0, C2 = -4, C3 = 8, τ = 1. Тогда

ì- 2t, t Î[0;1],

ì- t

2 + D , t Î[0;1],

t Î[1;3], Þ

t Î[1;3],

= í 2t

- 4,

= í t

- 4t + D2,

x1 = x2

+ 8,

t Î[3;4].

- t

2 + 8t + D ,

t Î[3;4].

î- 2t

Найдем неизвестные величины D1, D2 , D3 из краевых усло-

и условия непрерывности в точках t = 1 и

вий для функции x1(t)

t = 3:

x1(0) + x1(4) = 0 Þ D1 +16 + D3 = 0,

t= 1 Þ -1+ D1 = -3 + D2 ,

t= 3 Þ -3 + D2 = 15 + D3 .

Решая полученную систему линейных уравнений относительно D1, D2 , D3 , находим: D1 = 0, D2 = 2, D3 = -16, следовательно,

	ì- t2			, t Î[0;1],
ˆ ˆ	ï
ˆ ˆ	ï	t	2	- 4t + 2,	t Î[1;3],
x = x1	= í	t		- 4t + 2,	t Î[1;3],
	ï		2	+ 8t -16,	t Î[3;4].
	ï- t		2	+ 8t -16,	t Î[3;4].
	î

Проведем исследование полученного решения. Рассмотрим

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2118 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015553.47 Кб8metodichka_Arkh_EVM_k_rabota_2011g.doc
#
12.11.2019702.98 Кб4Metodichka_Dogovornoe_pravo.doc
#
10.05.2015697.34 Кб14Metodichka_Dogovornoe_pravo.doc
#
10.05.2015237.39 Кб12Metodika_Po_Oech_Diplomov.pdf
#
10.05.201561.44 Кб5Metodologia_portalov (2).doc
#
10.05.20151.01 Mб31Metody_optimizatsii_Shatina_A_V.pdf
#
10.05.20153.97 Mб9metod_ACM.doc
#
19.11.201993.7 Кб3Metod_ukaz2.doc
#
10.05.2015687.76 Кб17MIREA_Ekonomika_Metodichka_1076_2011.pdf
#
10.05.2015479.74 Кб25MIR_Kursovoy_proekt_Morina_A_I_ISB-3-12.doc
#
10.05.20153.2 Mб88mukrrtc2ssss011.doc