
Краткий курс математического анализа. Том 1
.pdf§ 8. Непрерывность элементарных функций |
147 |
Из свойств 2◦ и 3◦ показательной функции следуют соответствую-
щие свойства логарифма произведения и степени: |
|
lna xy = lna x + lna y, x > 0, y > 0, |
(8.27) |
lna xα = α lna x, x > 0, α R. |
(8.28) |
Докажем, например, формулу (8.28). Согласно свойству 3◦ пока-
зательной функции из теоремы 3 имеем |
|
|
|
(aβ )α = aβα, β R, α R. |
(8.29) |
||
Поэтому |
|
|
|
lna xα = lna(alna x)α |
= lna aα lna x |
= α lna x. |
|
(8.26) |
(8.29) |
(8.26) |
|
Из формул (8.27) и (8.28) следует формула для логарифма част-
ного: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
x |
= ln |
|
xy−1 |
= |
ln |
|
x + ln |
|
y−1 |
= |
ln |
|
x |
− |
ln y. |
|
a y |
a |
|
(8.27) |
|
a |
|
a |
|
(8.28) |
|
a |
|
a |
|||
С помощью перечисленных свойств показательной и логарифмической функций можно получить и другие их свойства.
Докажем, например, равенство
(ab)x = axbx, a > 0, b > 0.
В случае a = 1 или b = 1 написанное равенство очевидно. Если же a = 1 и b = 1, то
(ab)x = (aalna b)x =(a1+lna b)x = ax(1+lna b) =
(8.26) |
2◦ |
3◦ |
|
|
|
= axax lna b = axalna bx |
= axbx. |
|
|
(8.28) |
(8.26) |
8.3. Степенная функция. Функция y = xα, x > 0, называется
степенной функцией (α R).
Те о р е м а 4. При любом α R степенная функция xα непрерывна при всех x > 0.
Это сразу следует из того, что степенную функцию xα можно представить как композицию непрерывных функций — логарифмической и показательной. В самом деле, поскольку x = eln x, то
y = xα = eα ln x = eu, u = α ln x.
В точке x = 0 функция xα определена не для всех значений пока-
зателя α. Если α > 0, то существует предел lim xα = |
lim eα ln x = 0. |
x→+0 |
x→+0 |
По определению полагают |
|
0α = 0, α > 0. |
(8.30) |

148 Гл. 1. Дифференциальное исчисление функций одной переменной
Это определение согласуется с тем, что при рациональных α = r > 0 имеет место 0r = 0. Кроме того, естественность определения (8.30) оправдывается и тем, что, если в определении (8.7) взять a = 0 (раньше предполагалось, что a > 0), то будем иметь
0α = lim 0r = 0, α > 0.
r→α, r Q, r>0
При определении (8.30) функция xα оказывается непрерывной справа в точке x = 0 при любом α > 0.
Функция xα может оказаться определенной при некоторых рациональных α = 0 и для x < 0, например, x±n, x±1/(2n−1), n N.
Степенная функция xα непрерывна во всех точках, в которых она определена. Это следует из того, что если она определена при x < 0, то является четной или нечетной функцией.
8.4. Тригонометрические и обратные тригонометрические функции.
Л е м м а 2. Для любого действительного числа x имеет место неравенство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| sin x| |x|. |
(8.31) |
||||||
|
|
|
|
|
|
|
|
Рассмотрим на координатной плоско- |
||||||||||||||
|
|
|
|
|
|
|
|
сти круг радиуса R с центром в начале |
||||||||||||||
|
|
|
|
|
|
|
|
координат O. Если 0 x |
π |
, OA = R, |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
AOC = x (рис. 71), то |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 sin x = |
|AC| = |
|AB| |
|
|AB| |
= x, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
2R |
|
|
2R |
||
|
|
|
|
|
|
|
|
|
AB |
|
длина хорды, соединяющей точ- |
|||||||||||
|
|
|
|
|
|
|
|
где | |
и |
|
| — |
| |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ки |
A |
B, |
| |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
AB |
— длина дуги окружности, |
|||||||||||
соединяющей эти точки, а отношение |AB| |
равно радианной мере |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
угла AOB, т. е. равно 2x. Таким образом, неравенство (8.31) для |
||||||||||||||||||||||
случая 0 x |
π |
доказано. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
||||
Если − |
π |
x < 0, то 0 < −x |
, и потому по уже доказанному |
|||||||||||||||||||
2 |
2 |
|||||||||||||||||||||
| sin x| = sin(−x) −x = |x|, т. е. в |
этом случае неравенство (8.31) |
|||||||||||||||||||||
также справедливо. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Наконец, если |x| > |
π |
> 1, |
то неравенство (8.31) очевидно, ибо |
|||||||||||||||||||
2 |
||||||||||||||||||||||
| sin x| 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Те о р е м а 5. Функции y = sin x и y = cos x непрерывны на всей числовой оси.

|
|
§ 9. Сравнение функций |
|
|
|
|
|
|
149 |
|||||||||
Докажем, например, непрерывность функции y = sin x: |
||||||||||||||||||
| y| = | sin(x + x) − sin x| = 2 cos x + |
|
2x |
sin 2x |
| x|, (8.32) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ибо |
cos x + 2x |
|
|
sin |
|
|
|
|
|
|
|
|
||||||
|
1, |
|
2x | 2x|. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из неравенства |
(8.32) |
сразу |
следует, |
что |
|
lim |
|
y |
= 0; это и озна- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|||||
чает непрерывность функции y = sin x в произвольной точке x R. |
||||||||||||||||||
С л е д с т в и е. Функции tg x = |
sin x |
|
и ctg x = |
cos x |
непрерывны во |
|||||||||||||
cos x |
sin x |
|||||||||||||||||
всех точках числовой оси, |
|
|
|
|
|
|
|
|
|
|||||||||
кроме тех, |
в которых их знаменатели |
|||||||||||||||||
обращаются в нуль.
Это сразу следует из непрерывности частного непрерывных функций в точках, в которых делитель не обращается в нуль (см. следствие из свойства 6◦ пределов функций в п. 6.7).
Те о р е м а 6. |
Каждая |
из обратных |
тригонометрических |
|
функций |
y = arcsin x, y = arccos x, y = arctg x и y = arcctg x |
|||
непрерывна в области своего определения. |
|
|||
Это |
в силу |
теоремы о |
непрерывности |
обратных функций |
(см. п. 7.3) сразу следует из теорем 3 и 4. |
|
|||
8.5. Элементарные функции.
Те о р е м а 7. Каждая элементарная функция непрерывна в области своего определения.
В самом деле, согласно теоремам 1–6 все основные элементарные функции непрерывны на множествах, на которых они определены. Поэтому непрерывна в области своего определения и каждая функция, которая может быть получена из основных элементарных функций с помощью четырех арифметических действий и операции композиции функций, т. е. каждая элементарная функция (определение элементарной функции см. в п. 3.2).
§9. Сравнение функций
9.1.Замечательные пределы. В этом пункте будут вычислены пределы lim sin x , lim (1 + x)1/x, lim ln(1 + x) , lim ax − 1 , которые
x x→0 x→0 x x→0 x
обычно называются замечательными пределами. I. Докажем, что
lim |
sin x |
= 1. |
(9.1) |
|
|||
0 |
x |
|
|
x→ |
|
|
|
150 Гл. 1. Дифференциальное исчисление функций одной переменной
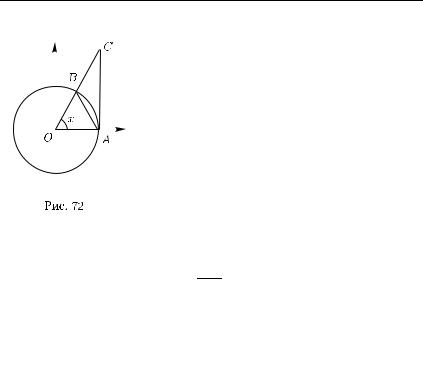
Рассмотрим в координатной плоскости круг радиуса R с центром |
|||||||||||||||||||||||
|
|
в начале координат. Если (рис. 72) OA = R, |
|||||||||||||||||||||
|
|
AOB = x, 0 < x < |
π |
, |
|
AC OA, |
то |
||||||||||||||||
|
|||||||||||||||||||||||
|
|
2 |
|||||||||||||||||||||
|
|
пл. |
OAB < пл. сектора OAB < пл. |
OAC, |
|||||||||||||||||||
|
|
т. е. |
1 |
R2 sin x < |
1 |
R2x < |
|
1 |
R2 tg x; отсюда |
|
|||||||||||||
|
|
|
|
2 |
|
||||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
sin x < x < tg x, |
|
|
|
||||||||||||||||
|
|
или |
1 < |
x |
< |
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
sin x |
|
|
cos x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|||||
|
|
В силу четности функций |
|
|
и |
|
|
это |
|||||||||||||||
|
|
|
sin x |
cos x |
|||||||||||||||||||
|
|
неравенство справедливо и для − |
π |
< x < 0. |
|||||||||||||||||||
|
|
2 |
|||||||||||||||||||||
Перейдя в этом неравенстве к пределу при x → 0 и заметив, что в силу непрерывности функции cos x при x = 0
имеет место равенство lim cos x = 1, получим
x→0
lim x = 1, x→0 sin x
что равносильно равенству (9.1). С помощью предела (9.1) вычисляется ряд других пределов, на-
пример, |
|
|
|
|
|
|
|
|
|
1 |
|
||
lim |
tg x |
= lim |
sin x |
· |
|
= 1, |
|||||||
|
|
|
x |
cos x |
|||||||||
x→0 x |
|
x→0 |
|
|
|||||||||
lim |
arcsin x |
|
= |
|
lim |
y |
= 1. |
||||||
|
|
||||||||||||
x→0 |
|
x |
x=sin y y→0 |
sin y |
|||||||||
II. Докажем, что |
lim (1 + x)1/x = e. |
(9.2) |
|||||||||||
|
|
|
|||||||||||
|
|
|
x→0 |
|
|
|
|
|
|
|
|
||
Мы уже знаем (см. п. 5.7), что |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
lim 1 + |
|
|
= e. |
|
|||||
|
|
|
|
n |
|
|
|||||||
Более того, из замечания 2 в п. 6.1 следует, что для любой последовательности nk N, nk → +∞, k = 1, 2, ..., также имеет место
равенство |
|
|
|
lim |
1 |
|
1 |
|
nk |
|
|
|
|
|
|
|
9 3 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
+ nk |
|
= e. |
|
|
|
( |
|||||||||||
|
|
|
|
k→∞ |
|
|
|
|
|
|
. ) |
||||||||||
|
xk > 0 и xk |
|
0, k = 1, 2, ... Положим nk = |
|
1 |
, где |
|
1 |
|
||||||||||||
Пусть |
→ |
xk |
xk |
— |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
целая часть числа |
|
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
xk |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
nk |
|
< nk + 1 |
|
|
|
(9.4) |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
и, следовательно, |
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
< xk |
1 |
|
|
|
|
(9.5) |
||||||||||
|
|
|
|
|
|
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
nk + 1 |
nk |
|
|
|
||||||||||||

|
|
|
|
|
§ 9. Сравнение функций |
|
|
|
|
|
|
|
|
|
151 |
||||||||||||||
Кроме того, согласно условию xk → 0 имеем |
1 |
|
→ ∞, откуда в силу |
||||||||||||||||||||||||||
xk |
|||||||||||||||||||||||||||||
неравенства (9.4) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
klim nk = +∞. |
|
|
|
|
|
|
|
|
|
(9.6) |
||||||||||
В результате имеем |
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
< (1 + xk)1/xk < 1 + nk |
|
|
, |
(9.7) |
|||||||||||||||||||||||
где |
|
1 + nk + 1 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
nk +1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
lim 1 |
+ |
1 |
|
|
|
nk +1 |
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
k |
→∞ |
|
|
nk + |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
lim 1 + |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= e, |
(9.8) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
k→∞ |
|
nk |
+ |
1 |
|
|
|
|
klim |
1 + |
|
|
|
(9.3) |
|
|||||||||||||
|
|
|
|
|
|
nk |
+ 1 |
|
|
||||||||||||||||||||
|
|
|
1 |
nk +1 |
|
|
|
|
|
|
|
|
→∞nk |
|
|
|
|
|
|
|
1 |
|
|
|
|||||
lim |
1 |
|
|
|
|
|
lim 1 |
|
|
1 |
|
|
|
lim |
1 |
|
|
|
= |
|
|||||||||
+ nk |
|
|
|
|
|
+ nk |
|
|
+ nk |
(9.9) |
|||||||||||||||||||
k→∞ |
|
|
= k→∞ |
|
k→∞ |
(9.3) e. |
|||||||||||||||||||||||
Из (9.7), (9.8) и (9.9) следует, что (см. обозначения в п. 6.6) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim (1 + x)1/x = e. |
|
|
|
|
|
|
|
|
|
(9.10) |
||||||||||
|
|
|
|
|
|
|
|
x→+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть теперь xk < 0 |
и xk → 0, k = 1, 2, ... Положим yk = −xk , |
||||||||||||||||||||||||||||
тогда yk > 0 и yk → 0, k = 1, 2, ... Без ограничения общности будем считать, что yk < 1 (с некоторого номера это неравенство заведомо выполняется). Имеем
lim (1 + x |
)1/xk = |
lim (1 |
− |
y )−1/yk = |
lim |
1 |
|
1/yk |
= |
|||||||||||
|
|
|
|
|||||||||||||||||
1 yk |
|
|
|
|||||||||||||||||
k |
→∞ |
k |
k |
→∞ |
|
|
k |
|
|
k |
→∞ |
|
|
|
|
|||||
= lim |
1 − yk + yk |
|
|
− |
|
|
|
|
= |
lim |
|
1 + |
yk |
|
− |
|
. (9.11) |
|||
|
|
|
|
|
|
(1 |
|
yk +yk )/yk |
|
|
|
|
− |
(1 |
yk )/yk +1 |
|||||
|
k→∞ |
|
|
|
|
|
|
|
|
|
k→∞ |
|
|
|
|
|
||||
|
|
1 − yk |
|
|
yk |
|
|
|
1 − yk |
|
|
|
||||||||
Положим теперь zk = |
|
. Очевидно, |
|
|
|
|
|
|||||||||||||
1 − yk |
|
|
|
|
(9.12) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
zk > 0, zk → 0. |
|
|
|
|
|||||||
Поэтому
lim (1 + xk)1/xk |
= |
lim (1 + zk)1/zk +1 = |
|
k→∞ |
(9.11) k→∞ |
|
|
|
|
= lim (1 + zk )1/zk |
lim (1 + zk ) |
|
|
k→∞ |
x→∞ |
Таким образом, |
|
|
|
|
lim (1 + x)1/x = lim (1 + x)1/x = e. |
||
x→+0 |
x→−0 |
(9.10) |
|
|
|
|
(9.13) |
= e. (9.13)
(9.10) (9.12)
Отсюда в силу теоремы 2 из п. 6.6 и следует равенство (9.2).

152 Гл. 1. Дифференциальное исчисление функций одной переменной
Вычислим с помощью (9.2) некоторые другие пределы. Покажем прежде всего, что
|
|
lim |
lna(1 + x) |
|
= |
1 |
|
|
, a > 0, |
a = 1, |
|
(9.14) |
|||||||||||||||
|
|
x |
ln a |
|
|||||||||||||||||||||||
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
в частности, |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
lim |
|
ln(1 + x) |
= 1. |
|
|
(9.15) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
В самом деле, |
|
x→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
lna(1 + x) |
= lim lna(1 + x)1/x = lna lim (1 + x)1/x = lna e = |
|
1 |
. |
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
0 |
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
ln a |
|
||||||||
x→ |
|
|
x→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ |
|
|
|
|
|
|
|
|||
Докажем еще, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
lim |
|
ax − 1 |
= ln a, |
|
a > 0, |
a = 1, |
|
(9.16) |
||||||||||||||||
|
|
|
x 0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в частности, что |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
lim |
ex − 1 |
= 1. |
|
|
|
|
(9.17) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x→ |
|
|
|
|
|
|
|
|
|
ln(1 + y) |
|
|||||||||
Действительно, положив y = ax − 1 и, следовательно, x = |
, |
||||||||||||||||||||||||||
|
ln a |
||||||||||||||||||||||||||
получим lim y = 0, а поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x→0 |
|
|
ax − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
lim |
= lim |
|
y ln a |
= |
ln a. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x→0 |
|
x |
|
y→0 ln(1 + y) |
(9.15) |
|
|
|
|
|
|
|||||||||||||
9.2. Сравнение функций в окрестности заданной точки.
Как известно, сумма, разность и произведение бесконечно малых являются бесконечно малыми. Частное же бесконечно малых может быть и не бесконечно малой, однако отношение бесконечно малых позволяет сравнивать их «по порядку убывания». Аналогично можно сравнивать «по порядку роста» бесконечно большие. Перейдем к точным определениям.
Пусть функции f и g заданы на множестве X и x0 — конечная или бесконечная удаленная точка прикосновения этого множества. При этом возможны случаи, когда x0 X и когда x0 X.
Будем предполагать, что существуют такие окрестность U = U (x0) точки x0 и функция ϕ, заданная на X ∩ U , что для всех x X ∩ U выполняется равенство
f (x) = ϕ(x)g(x). |
(9.18) |
В частности, если функции f и g заданы в точке x0, то и функция ϕ задана в этой точке, а если f и g не заданы в ней, то не задана в ней
ифункция ϕ.
Оп р е д е л е н и е 1. Функция f называется функцией, ограниченной относительно функции g в окрестности точки x0, если функ-
ция ϕ ограниченна.
§ 9. Сравнение функций |
153 |
Вэтом случае существует такая постоянная c > 0, что для всех x X ∩ U выполняется неравенство
|ϕ(x)| c, |
|
(9.19) |
|||
а следовательно, и неравенство |
|
|
|
|
|
f (x) |
| |
|
c g(x) . |
(9.20) |
|
| |
(9.18) |
| |
| |
|
|
|
|
(9.19) |
|
|
|
Условие (9.20) равносильно условиям (9.18) и (9.19). Действительно, если выполняется условие (9.20), то при
|
|
f (x) |
, |
если |
g(x) = 0, |
ϕ(x) = |
g(x) |
||||
|
|
|
|
если |
g(x) = 0, |
|
0, |
|
|||
выполняются условия (9.18) и (9.19).
Если функция f ограничена относительно функции g в окрестности точки x0, то пишут
f = O(g), x → x0 |
(9.21) |
(читается: f есть «O большое» от g).
О п р е д е л е н и е 2. Функция f называется функцией того же порядка при x → x0, что и функция g, если существуют такие посто-
янные c1 > 0 и c2 > 0, что для всех x X ∩ U выполняется неравенство
c1 |ϕ(x)| c2. |
(9.22) |
В этом случае для всех x X ∩ U выполняется неравенство |
|
c1|g(x)| |f (x)| c2|g(x)|. |
(9.23) |
Если функция f того же порядка при x → x0, что и функция g, то
пишут f = g, x → x0.
Очевидно, что функция f того же порядка при x → x0, что и функ-
ция g, тогда и только тогда, когда f = O(g) и g = O(f ), x → x0.
О п р е д е л е н и е 3. Функция f называется бесконечно малой относительно функции g при x → x0, если функция ϕ бесконечно малая
при x → x0, т. е. если |
lim ϕ(x) = 0. |
(9.24) |
|
В этом случае пишут |
x→x0 |
|
|
f = o(g), x → x0 |
(9.25) |
||
|
(читается: f есть «o малое» от g при x → x0).

154Гл. 1. Дифференциальное исчисление функций одной переменной
Оп р е д е л е н и е 4. Функция f называется эквивалентной функции g (или асимптотически равной ей) при x → x0, если
|
|
|
lim ϕ(x) = 1. |
|
|
(9.26) |
В этом случае пишут |
x→x0 |
|
|
|
||
|
|
|
|
|||
|
|
f g, x → x0. |
|
|
|
|
З а м е ч а н и е 1. Если x0 |
X, то, как известно (см. п. 6.2), из суще- |
|||||
ствования предела |
lim ϕ(x) следует, что |
lim ϕ(x) = ϕ(x0). Поэтому |
||||
|
|
x→x0 |
x→x0 |
|
|
|
в случае (9.24) имеем ϕ(x0) = 0, а в случае (9.26) — ϕ(x0) = 1. |
||||||
Если |
f = o(g), |
x → x0 и |
lim g(x) = 0, |
то функция |
f |
называется |
|
x x0 |
|
||||
|
|
|
→ |
|
|
|
бесконечно малой более высокого порядка, чем бесконечно малая g.
В случае f = o(gn), x → x0, бесконечно малую f называют бесконечно малой порядка n относительно бесконечно малой g.
З а м е ч а н и е 2. Если в условиях определений 3 или 4 функция g не обращается в нуль на множестве X ∩ U и x0 X, то условие (9.24)
можно записать в виде |
f (x) |
|
|
||
lim |
= 0, |
(9.27) |
|||
|
|
||||
x→x0 |
g(x) |
|
|||
а условие (9.26) — в виде |
|
|
|
|
|
lim |
f (x) |
= 1. |
(9.28) |
||
x→x0 |
g(x) |
|
|||
З а м е ч а н и е 3. Если x0 X и существует конечный предел |
|||||
lim |
f (x) |
= k, |
(9.29) |
||
|
|||||
x→x0 |
g(x) |
|
|||
то функция f (x) ограничена на пересечении некоторой окрестности g(x)
U (x0) точки x0 с множеством X (см. свойство 1◦ пределов функций в п. 6.7), т. е. существует такая постоянная c > 0, что для всех x X ∩
∩ U (x0) выполняется неравенство fg((xx)) c, т. е.
|f (x)| c|g(x)|,
откуда следует, что при выполнении условия (9.29) имеет место соот-
ношение
f (x) = O(g(x)), x → x0.
З а м е ч а н и е 4. В определениях 1–4 функции f и g могут быть последовательностями f = {xn}, g = {yn}, и, таким образом, указанные определения содержат в себе определения следующих понятий:
а) последовательности, ограниченной относительно другой после-
довательности: xn = O(yn), n → ∞;
б) последовательностей одного порядка: xn = yn, n → ∞;
в) асимптотически равных последовательностей: xn yn, n → ∞;
§ 9. Сравнение функций |
155 |
г) последовательности, бесконечно малой по сравнению с другой
последовательностью: xn = o(yn), n → ∞. |
|
П р и м е р ы. 1. sin 2x = O(x), x → 0, ибо |
|
| sin 2x| 2|x|. |
(9.30) |
Верно и соотношение x = O(sin 2x), x → 0, ибо существует конеч-
ный предел lim |
x |
|
= |
1 |
, и, следовательно, функция |
x |
|
ограни- |
sin 2x |
|
sin 2x |
||||||
0 |
2 |
|
|
|||||
x→
чена в некоторой окрестности U (0) точки x = 0 (см. свойство 1◦ пределов функций в п. 6.7). Иначе говоря, существует такая постоянная
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
c sin 2x , |
x U (0). |
|
|
(9.31) |
|||
c > 0, что для всех |
x |
|
U (0) |
выполняется неравенство |
sin 2x |
|
|
c, |
||
x = 0, поэтому |
|
| |
| |
|
|
|||||
|
| | |
|
|
|
|
|
||||
Из (9.30) и (9.31) следует, что при x → 0 функции y = x и y = sin 2x
одного порядка: |
|
|
|
|
sin 2x = x, |
|
x → 0. |
||||||||||
|
|
|
|
|
|
|
|||||||||||
2. |
x3 = o(x2), |
x |
→ |
0, |
ибо |
x3 |
= x |
· |
x2 |
и |
lim x = 0. |
||||||
|
|
|
|
|
|
|
x |
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|||
3. x2 = o(x3), |
x → ∞, ибо x2 = |
1 |
· x3 |
и |
xlim |
1 |
= 0. |
||||||||||
x |
x |
||||||||||||||||
|
|
lim |
sin x |
|
|
|
|
|
|
|
→∞ |
||||||
4. Поскольку |
= 1, |
то функции |
y = x и y = sin x экви- |
||||||||||||||
|
|||||||||||||||||
|
|
x 0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
валентны при x → 0: |
|
|
sin x x, |
|
x → 0. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
З а м е ч а н и е 5. |
Символы O(g) |
и o(g) по существу обозначают |
|||||||||||||||
целые классы функций, обладающих по сравнению с данной функцией определенным свойством, поэтому равенства типа f (x) = O(g(x)) и f (x) = o(g(x)), x → x0, следует читать только слева направо, например, x2 = o(x), x → 0. Здесь верно то, что функция y = x2 является при x → 0 бесконечно малой по сравнению с функцией y = x, но не всякая функция, бесконечно малая по сравнению с функцией y = x, является функцией y = x2, т. е. o(x) = x2. Иначе говоря, равенства с символом «o малое», как и равенства с символом «O большое» не обладают свойствами симметричности. Эти равенства не обладают и свойством транзитивности:
x2 = o(x), x3 = o(x),
но x2 = x3.
9.3. Эквивалентные функции. Примеры эквивалентных функций (см. определение 3 в п. 9.2) легко получить из результатов в п. 9.1:
x sin x tg x arcsin x arctg x ln(1 + x) ex − 1, x → 0.

156Гл. 1. Дифференциальное исчисление функций одной переменной
Те о р е м а 1. Для того чтобы функции f (x) и g(x) были эквивалентны при x → 0, необходимо и достаточно, чтобы
f (x) = g(x) + o(g(x)), x → 0. |
(9.32) |
Формула (9.32) является просто другой записью определения 4.
Действительно, |
условие |
(9.26) |
lim ϕ(x) = 1 равносильно |
усло- |
вию ϕ(x) = 1 + |
ε(x), где |
x→x0 |
|
|
lim ε(x) = 0. Поэтому условие |
|
|||
|
x→x0 |
|
|
|
|
f (x) = ϕ(x)g(x), |
lim ϕ(x) = 1, |
(9.33) |
|
равносильно условию |
|
x→x0 |
|
|
|
|
|
||
f (x) = (1 + ε(x))g(x) = g(x) + ε(x)g(x), lim ε(x) = 0, |
(9.34) |
|||
|
|
|
x→x0 |
|
т.е. условию f (x) = g(x) + o(g(x)), x → x0.
За м е ч а н и е 1. Если g(x) = 0, x X, x = x0, то условие (9.32) можно записать в виде
lim f (x) − g(x) = 0.
x→x0 g(x)
Оно означает, что относительная погрешность f (x) − g(x) между экви- g(x)
валентными функциями f и g является бесконечно малой при x → x0. |
|||||||||||
П р и м е р 5. ctg x = |
1 |
|
+ o |
1 |
, x → 0. Чтобы в1 |
этом убедиться, |
|||||
x |
x |
||||||||||
в силу теоремы 1 достаточно показать, что ctg x |
|
, x → 0. Это же |
|||||||||
x |
|||||||||||
сразу следует из того, что lim |
tg x |
= 1 (см. п. 9.1), ибо |
|||||||||
0 |
|
|
x |
|
|
|
|||||
|
|
x→ |
|
|
|
|
|
|
|
||
lim |
ctg x |
= lim |
x = 1. |
|
|||||||
|
|
||||||||||
x→0 1/x |
|
|
x→0 |
tg x |
|
||||||
Те о р е м а 2. Если f (x) f1(x), g(x) g1(x), x → x0, то пределы
(конечные или бесконечные) |
lim |
f (x) |
и |
lim |
f1 |
(x) |
одновременно су- |
|
|
g1 |
(x) |
||||||
|
x→x0 |
g(x) |
x→x0 |
|
||||
ществуют или нет, при этом, если они существуют, то они равны |
||||||||
lim |
f (x) |
= lim |
f1(x) . |
|
|
(9.35) |
||
|
|
|
||||||
x→x0 |
g(x) |
x→x0 |
g1(x) |
|
|
|
||
Условия f f1 и g g1, x → x0 означают, что существуют такие окрестность U = U (x0) и функции ϕ и ψ, определенные на пересечении X ∩ U , что
f (x) = ϕ(x)f1(x), |
g(x) = ψ(x)g1(x), x X ∩ U , |
(9.36) |
lim ϕ(x) = lim ψ(x) = 1. |
(9.37) |
|
x→x0 |
x→x0 |
|
