Краткий курс математического анализа. Том 2

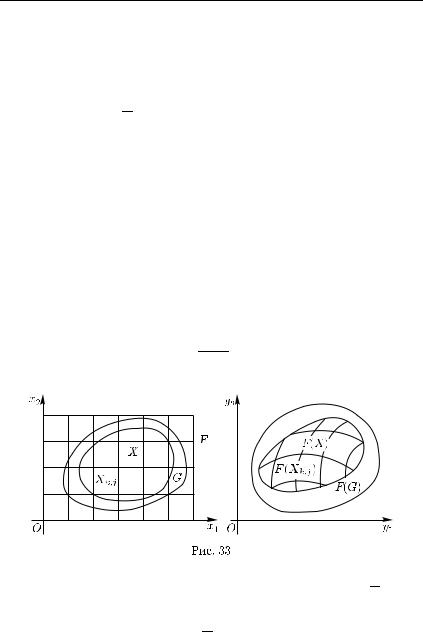
180 Гл. 5. Интегральное исчисление функций многих переменных

Если теорема 1 справедлива для двух неотрицательных функций f1(y) = f (y) + c и f2(y) = c, то она в силу свойства линейности интеграла справедлива и для функции

f (y) = f1(y) − f2(y).

Обозначим через Xk,j, j = 1, 2, ..., jk, всевозможные непустые пересечения замыкания X множества X с кубами ранга k. Таким образом, для каждого j = 1, 2, ..., jk существует такой куб ранга k, обозначим его Qk,j , что

образуют разбиения замыкания F (X) множества F (X) (рис. 33), мелкости которых также стремятся к нулю.

Действительно, элементы Xk,j разбиения τk являются измеримыми компактами как пересечения двух измеримых компактов X и Qk,j , лежащих в открытом множестве G, поэтому согласно лемме 6 их образы F (Xk,j) являются измеримыми множествами. Из того, что τk является разбиением множества X, следует, что

182 Гл. 5. Интегральное исчисление функций многих переменных

Отберем те из множеств F (Xk,j), которые не пересекаются с границей ∂F (X) множества F (X). В силу свойств отображения F (см., в частности, (44.44)) это равносильно выбору тех множеств Xk,j, ко-

торые не пересекаются с границей ∂X множества X. Для таких множеств Xk,j имеем

т. е. множество Xk,j является в этом случае кубом ранга k. Действительно, в силу условия (44.53 ) в кубе Qk,j имеется точка

компакта X. Если бы этот куб не содержался в X, то в нем нашлась бы точка, не принадлежащая X, а поэтому и точка x, принадлежащая его границе: x ∂X X (см. замечание 8 в п. 42.1). Таким образом,

x X ∩ Qk,j = Xk,j и x ∂X,

что противоречит выбору множества Xk,j.

Выберем теперь произвольным образом по точке η(j,k) в каждом из отобранных множеств F (Xk,j) разбиения F (τk). В силу включения

Xk,j ∩∂X=

Соответствующая этой интегральной сумме неполная интеграль-

Xk,j ∩∂X=

Заметим, что функция f , будучи непрерывной на компакте F (X), ограничена на нем:

Оценим неполную интегральную сумму σF (τk )(∂F (X)) с помощью неравенства (44.48):

Первое слагаемое в правом части этого неравенства является неполной интегральной суммой (44.65), а второе в силу выполнения условия (44.49) стремится к нулю при k → ∞ (здесь h = 10−k):

lim α(10−k) = 0.

k→∞

Мелкости разбиений τk и F (τk) стремятся к нулю при k → ∞ (см. (44.55) и (44.59)), поэтому, согласно теореме 4 п. 42.5, рассматриваемые неполные интегральные суммы стремятся при k → ∞ к соот-

Перейдя к пределу при k → ∞ в неравенстве (44.67), получим

Теперь заметим, что отображение F −1, обратное данному отображению F , также непрерывно дифференцируемо, взаимно однозначно, а его якобиан JF −1 (y) не обращается в нуль на открытом множестве F (G), и для него имеет место формула (см. п. 40.4)

Для отображений F и F −1 имеет место равенство

так как отображение F F −1 является тождественным отображением множества F (G) на себя.

184 Гл. 5. Интегральное исчисление функций многих переменных

Применим к интегралу, стоящему в правой части неравенства (40.69), само это неравенство для отображения F −1. Это можно сделать, ибо для обратного отображения F −1 выполняются все условия теоремы. Заметив, что X = F −1(F (X)), получим

в п. 42.7), формулу (44.50) замены переменных в кратном интеграле можно обобщить на более широкий класс отображений, отказавшись от взаимной однозначности отображения и неравенства нулю якобиана отображения на границе области интегрирования.

Для того чтобы сформулировать это обобщение, нам понадобится понятие непрерывной продолжаемости отображения, в частности непрерывной продолжаемости функции.

Непрерывное отображение множества в некоторое пространство называется непрерывно продолжаемым на замыкание множества,

если существует непрерывное отображение этого замыкания в то же пространство, совпадающее на самом множестве с данным отображением.

Непрерывные продолжения отображений и числовых функций будем обозначать теми же символами, что и продолжаемые отображения и функции.

Те о р е м а 2. Если отображение F : G → Rny открытого измеримого множества G Rnx на открытое измеримое множество G Rny взаимно однозначно, непрерывно дифференцируемо, его якобиан не обращается в нуль на G, если отображение F и его якобиан непрерывно продолжаемы на замыкание G множества G, а функция f непрерывна на множестве G и непрерывно продолжаема не его замыкание G , то

Таким образом, в условиях теоремы непрерывное продолжение отображения F может и не быть взаимно однозначным на границе ∂G области интегрирования G, а непрерывное продолжение якобиана может на этой границе обращаться в нуль.

Замыкание G измеримого множества G является измеримым компактом, на который по условию теоремы непрерывно продолжаема функция f , поэтому это продолжение интегрируемо на компакте G , а следовательно, сама функция f интегрируема на открытом множестве G . В силу же непрерывной продолжаемости отображения F и его якобиана на замыкание G множества G, рассуждая аналогичным образом, получим, что функция f (F (x))|JF (x)| интегрируема на открытом множестве G. Таким образом, интералы, стоящие как в левой, так и в правой части равенства (44.73), в условиях теоремы существуют.

Множество G открыто и измеримо. Поэтому существует последовательность таких измеримых открытых множеств Gk, k = 1, 2, ..., что (см. замечание 4 в п. 42.7)

Ясно, что замыкание Gk множества Gk является компактом. При-

ты, и для них в силу условий (44.74) и (44.75) выполняются условия

Из (44.74) и (44.75) в силу возможности предельного перехода при k → ∞ в равенстве (44.77) (см. свойство 9 в п. 42.7) следует, что

Поэтому, перейдя к пределу при k → ∞ в равенстве (44.77), получим формулу (44.73).

44.4. Геометрический смысл абсолютной величины якобиана отображения. Пусть F — непрерывное дифференцируемое

взаимно однозначное отображение открытого измеримого множества

186 Гл. 5. Интегральное исчисление функций многих переменных

G Rnx на открытое измеримое множество G Rny : F (G) = G . Пусть якобиан JF отображения F не обращается в нуль на G, и пусть как отображение F , так и его якобиан непрерывно продолжаемы на замыкание G множества G. Как и раньше, будем эти продолжения

обозначать соответственно F и JF , называя продолженную функцию JF по-прежнему якобианом отображения F .

Пусть D — измеримая область, т. е. измеримое линейно связное открытое множество, содержащееся в замыкании G открытого множества G:

D G.

Таким образом, в некоторых точках области D якобиан отображения может обращаться в нуль. Это может происходить в тех точках, которые принадлежат границе открытого множества G. При-

мером такой точки является точка (0, 0) для проколотого круга

G = {(x1, x2) : x21 + x22 < 1} \ {(0, 0)} и круга D = {(x1, x2) : x21 + x22 < < 1/2}.

Пусть образ F (D) замыкания D области D является измеримым множеством. Для его меры имеет место формула (см. свойство 1◦ кратного интеграла в п. 42.1)

μF (D) = dy.

F (D)

Применив к интегралу, стоящему в правой части этого равенства, формулу замены переменного в кратном интеграле (здесь f (y) = 1), получим

μF (D) = |JF (x)| dx.

D

Если {D} — семейство указанных областей, содержащее области сколь угодно малого диаметра, и если существует точка x(0), принадлежащая всем областям этого семейства, то

188 Гл. 5. Интегральное исчисление функций многих переменных

координатных линий в этом случае имеют вид

т. е. представляют собой параметрически заданные плоские кривые.

обратное к отображению (44.84), определено на некотором открытом

P = {(x, y) : x = x(u, v), y = y(u, v); u0 < u < u0 +Δu, v0 < v < v0 + v}

(P называется координатным параллелограммом), и пусть M0 =

= (x0, y0), x0 = x(u0, v0), y0 = y(u0, v0).

Если рассмотреть вспомогательную плоскость u, v, то на ней нера-

при отображении (44.85) границы прямоугольника P , которая, как и граница всякого прямоугольника, является кусочно-гладкой кривой и, следовательно, имеет площадь, равную нулю (см. теорему 3 в п. 42.2). Отсюда вытекает согласно лемме 4 п. 44.2, что и площадь ее образа, т. е. площадь множества ∂P , также равна нулю. Поэтому к координатному параллелограмму P можно применять формулу (44.82). Согласно интегральной теореме о среднем существует такая точка

Это обстоятельство часто используется на практике при вычислении якобианов преобразований криволинейных координат в декартовы.

Из криволинейных координат на плоскости отметим полярные координаты r, ϕ, связанные с декартовыми x, y соотношениями

Координатными линиями полярных координат являются окружности r = const и лучи, выходящие из начала координат, ϕ = const.

В этом случае координатные линии пересекаются под прямыми

углами (когда имеет место такое обстоятельство, то говорят, что криволинейные координаты ортогональны).