Занятие 7(Фдз 8)

21

Занятие 7 (Фдз 8).

Линейный оператор простого типа.

7.1. Определение линейного оператора простого типа, диагонализуемость его матрицы. Достаточное условие оператора простого типа. Примеры линейных операторов простого типа (операторы задачи 3 из типового расчета).

7.1. По определению, линейный оператор называется оператором простого типа (или простым оператором), если из собственных векторов этого оператора можно составить базис линейного пространства . Такой базис называется собственным базисом оператора .

Если оператор простого типа, и - собственный базис этого оператора, то матрица этого оператора в этом базисе является диагональной

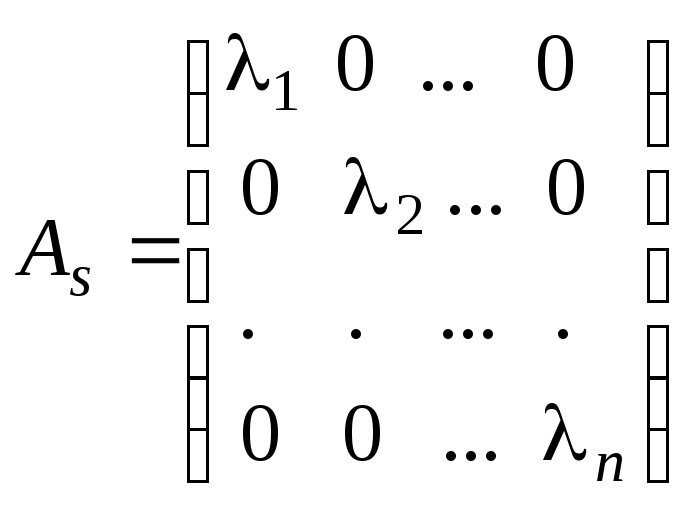, (1)

где - собственные значения оператора , соответствующие собственным векторам , т.е. .

Пример 1. Рассмотрим линейный оператор , действующий в линейном пространстве векторов декартова пространства следующим образом: проектирует каждый вектор на плоскость . Покажем, что данный оператор – оператор простого типа.

Решение.

Собственные значения и собственные векторы найдены ранее в примере 3 занятия 5.

Этот оператор имеет собственное значение , соответствующие ему собственные векторы параллельны оси . Кроме этого оператор имеет собственное значение , соответствующие ему собственные векторы параллельны плоскости .

Из собственных векторов этого оператора можно составить базис пространства .

Например, векторы (где - единичный вектор оси , - единичные векторы осей и ) – образуют собственный базис оператора . Действительно, тройка служит базисом пространства и все эти векторы – собственные векторы оператора , т.к. .

Если - оператор простого типа, то все его собственные значения вещественны. Это условие представляет необходимое условие простоты оператора .

Однако вещественность всех собственных значений линейного оператора не служит достаточным условием простоты этого оператора.

Пример 2. Рассмотрим линейный оператор из примера 5 занятия 6. , .

Покажем, что данный оператор не является простым оператором.

Решение.

Все собственные значения оператора равны нулю (см. пример 5 из занятия 6). Таким образом, необходимое условие простоты линейного оператора выполнено.

Однако из множества всех собственных векторов этого оператора нельзя составить базис пространства . Действительно, множество представляет линейную оболочку линейно независимых многочленов , следовательно, . Пространство трехмерно, т.к. оно имеет стандартный базис .

Чтобы из системы получить базис пространства , нужно к этой системе добавить многочлен , в котором . Никакой из многочленов не является собственным многочленом данного линейного оператора. Поэтому, оператор не имеет собственного базиса, и значит, не является простым оператором.

Достаточное условие того, чтобы заданный оператор был оператором простого типа, формулируются в виде следующей теоремы.

Теорема. Если все собственные значения линейного оператора действительны и различны, то оператор - оператор простого типа.

Пример 3. Линейный оператор действует в двумерном линейном пространстве . В базисе этого пространства оператор имеет матрицу . Доказать, что оператор - оператор простого типа. Найти собственный базис и матрицу оператора в этом базисе.

Решение.

Действие оператора в базисе определяется равенством , где координаты вектора и - координаты вектора в базисе .

Собственные значения оператора найдем из характеристического уравнения.

.

Собственные значения оператора - действительные и различные числа. Следовательно, выполнено достаточное условие, доказывающее простоту оператора .

Найдем теперь собственный базис оператора .

- собственный вектор оператора .

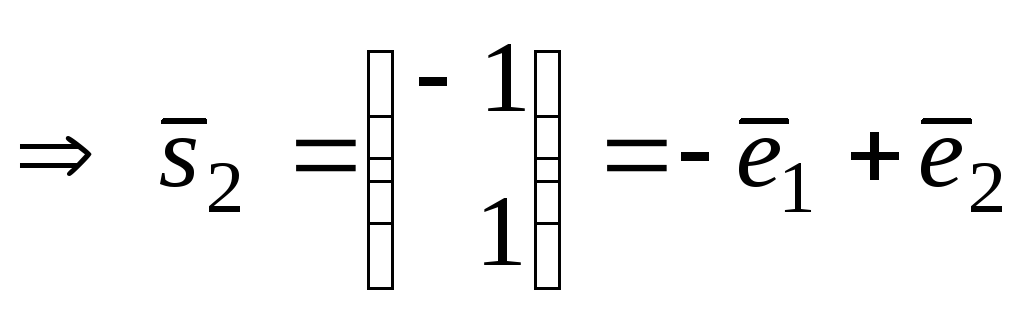- другой собственный вектор оператора .

Собственные векторы отвечают различным собственным значениям. Следовательно, эти векторы дают линейно независимую систему. Поскольку , векторы образуют базис пространства . Это – собственный базис оператора .

Осталось найти матрицу оператора в собственном базисе .

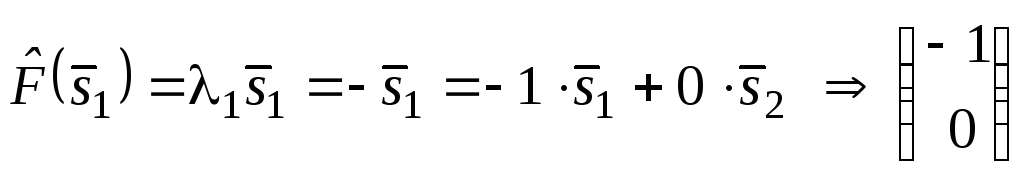- первый столбец матрицы .

- второй столбец матрицы .

. Эта же матрица получается из формулы (1).

Пример 4. Линейный оператор действует в линейном пространстве

по правилу .

Требуется выяснить, является ли данный оператор оператором простого типа. Если да, то найти матрицу оператора в собственном базисе.

Решение.

- линейная оболочка трех линейно независимых функций , служащих базисом пространства . .

Найдем матрицу оператора в базисе .

- первый столбец .

- второй столбец .

-

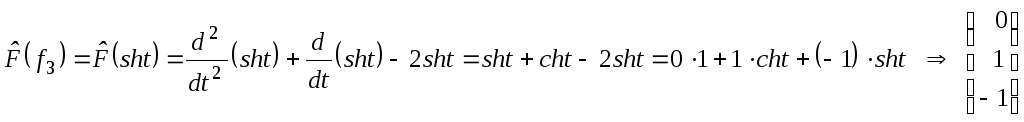третий столбец . Следовательно,

.

С помощью этой матрицы найдем собственные значения оператора.

.

Необходимое условие оператора простого типа выполнено (все собственные значения вещественные числа), а достаточное условие нет (есть одинаковые собственные значения: ).

Найдем собственные функции оператора.

- собственная функция оператора, отвечающая собственному значению .

- собственные функции оператора, отвечающие собственному значению .

Собственные функции линейно независимы и служат базисом пространства . Следовательно, оператор имеет собственный базис, и он является оператором простого типа.

Матрица оператора в собственном базисе сразу же находится по формуле (1).

.

Пример 5. Дано множество матриц и преобразование , действующее на этом множестве по правилу , где .

Доказать, что - линейный оператор простого типа и найти матрицу этого оператора в собственном базисе.

Решение.

1) , где .

- линейная оболочка матриц в линейном пространстве матриц . Следовательно, - линейное подпространство в пространстве .

2) .

Значит, - оператор.

3) Пусть - произвольные матрицы из множества и

- произвольные числа. .

Следовательно, - линейный оператор.

4) Матрицы образуют базис в пространстве . . Найдем матрицу этого оператора в базисе .

- первый столбец матрицы .

- второй столбец матрицы .

- третий столбец матрицы .

.

5) Теперь найдем собственные значения и собственные матрицы оператора .

.

Все собственные значения действительны и различны. Согласно достаточному условию

- линейный оператор простого типа.

6) Найдем собственный базис оператора .

- собственная матрица оператора .

- собственная матрица оператора .

- собственная матрица оператора .

7) - собственный базис оператора .

- матрица оператора в собственном базисе.

_______________________________________________________________________

Домашнее задание.

1. Показать, что заданные линейные операторы являются оператороми простого типа, найти их собственный базис и матрицу в собственном базисе.

1.1. , .

1.2.. , , .