Занятие 11(Фдз 12)

28

Занятие 11 (Фдз 12).

Определение евклидова пространства. Примеры евклидовых пространств.

Матрица Грама. Ортогональный и ортонормированный базисы.

11.1. Определение евклидова пространства. Примеры евклидовых пространств.

11.2. Координатная и векторно-матричная запись скалярного произведения в заданном базисе. Матрица Грама и ее свойства. Преобразование матрицы Грама при переходе к новому базису.

11.3. Ортогональная система векторов. Ортогональный и ортонормированный базисы. Матрица Грама, запись скалярного произведения векторов и длин векторов в этих базисах.

11.1. Определение. Евклидовым пространством называется линейное пространство , на котором определена билинейная функция , удовлетворяющая требованиям:

1. ;

2. , причем ;

Требование 1 означает, что - симметричная билинейная функция.

Требование 2 означает, что соответствующая билинейной функции квадратичная функция является положительно определенной.

Билинейная функция с требованиями 1, 2 называется скалярным произведением (или евклидовой структурой в линейном пространстве ) и далее обозначается .

Из 1, 2 выводятся следующие важные неравенства:

- неравенство треугольника;

- неравенство Коши-Буняковского.

Далее, по определению

называется длиной вектора ,

а угол , найденный из формулы , называется углом между векторами .

После сделанного определения длины вектора неравенство треугольника и неравенства Коши-Буняковского перепишутся в виде:

- неравенство треугольника;

или - неравенство Коши-Буняковского.

Данное определение скалярного произведения обобщает введенное в 1-м семестре определение скалярного произведения в векторных пространствах формулой .

Следует подчеркнуть, что в новом определение длина и угол выводятся из скалярного произведения, тогда как в старом определении наоборот, скалярное произведение определяется через длины векторов и угол между ними.

Рассмотрим несколько примеров.

Пример 1. Пусть - линейное пространство многочленов степени не выше второй степени. - стандартный базис этого пространства. Пусть - симметричная билинейная функция. Ее значения на базисных многочленах:

.

Доказать, что билинейная функция является скалярным произведением в пространстве . Найти: скалярное произведение "векторов" ,;

длины этих "векторов" и угол между ними.

Решение. Сначала докажем, что является скалярным произведением.

Требование 1 выполнено по условию. Проверим выполнение требования 2.

Возьмем два произвольных многочлена и .

. (1)

Таким образом, функция представлена симметричной билинейной формой на координатах многочленов и в базисе . (1)

. (2)

Это - квадратичная форма, соответствующая симметричной билинейной форме (1).

В матричном виде эта квадратичная форма перепишется так.

, где - матрица квадратичной формы (2) и симметричной билинейной формы (1) одновременно.

С помощью критерия Сильвестра исследуем квадратичную форму на положительную определенность.

- положительно определенная функция требование 2 выполнено.

Тем самым доказано, что рассмотренная билинейная функция является скалярным произведением в линейном пространстве , а само пространство становится евклидовым пространством.

Вычислим теперь скалярное произведение для заданных "векторов" , и найдем их "длины" и "угол" между ними.

В базисе "векторы" , имеют соответственно координаты . По формуле (1) находим

.

По формуле (2) получаем

- длина "вектора" .

- длина "вектора" .

- "угол" между и .

Пример 2. Рассмотрим множество . - двумерное линейное пространство с базисом . Пусть - билинейная функция. Ее значения на базисных матрицах таковы: .

Доказать, что - евклидово пространство и найти скалярное произведение матриц , их "длину" и угол между ними.

Решение. Сначала докажем, что является скалярным произведением.

Начнем с проверки требования 1.

Возьмем две произвольные матрицы из пространства .

В базисе эти матрицы имеют координаты .

.

.

. (3)

- симметричная билинейная функция, представленная в базисе симметричной билинейной формой (3). Итак, требование 1 выполнено.

Теперь проверим требование 2.

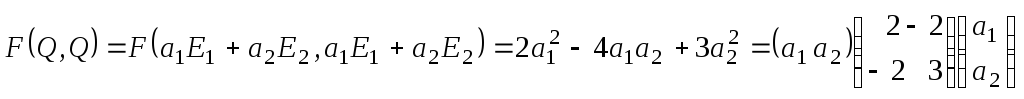- квадратичная форма, соответствующая билинейной форме (3). Из матрицы квадратичной формы находим ее угловые определители . Квадратичная форма положительно определена. Требование 1 выполнено.

Требования 1, 2 выполнены - евклидово пространство со скалярным произведением .

В базисе координаты заданных матриц равны .

.

.

.

.

11.2. Пусть - - мерное евклидово пространство, - базис пространства , тогда скалярное произведение векторов вычисляется по формуле

или , (1)

где , - вектор строка, - вектор столбец из координат векторов в базисе .

Первое и второе равенства в формуле (1) называется координатной записью скалярного произведения и соответственно векторно-матричной записью скалярного произведения в заданном базисе .

Матрица называется матрицей Грама. Эта матрица обладает тем свойством, что все ее угловые определители строго положительны, т.е.

.

Матрицы Грама и , отвечающие базисам и соответственно, связаны между собой по формуле

, (2)

где - матрица перехода от базиса к базису . Эта формула служит правилом, по которому преобразуется матрица при переходе к новому базису.

Пример 3. Пусть - трехмерное евклидово пространство, и в базисе матрица Грама равна , , . Вычислить скалярное произведение , найти длины векторов и угол между ними.

Решение.

В базисе скалярное произведение вычисляется по формуле , где - координаты векторов в этом базисе. Следовательно,

.

.

.

.

Пример 4. Пусть - линейное пространство многочленов степени не выше второй степени. - стандартный базис этого пространства. В примере 8 занятия 10 доказано, что симметричная билинейная функция со следующими значениями на базисных многочленах:

является скалярным произведением. Поставим задачей найти матрицу Грама, координатную и векторно-матричную запись скалярного произведения в указанном стандартном базисе пространства .

Решение.

- скалярное произведение в . - базис .

, , .

, , .

- матрица Грама в базисе .

Пусть . - вектор строка, - вектор столбец из координат многочленов в базисе .

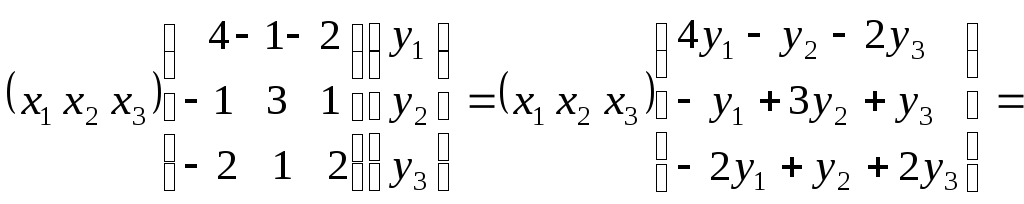
- векторно-матричная запись скалярного произведения в базисе .

.

. - координатная запись скалярного произведения в базисе .

Пример 5. Рассмотрим множество . - двумерное линейное пространство с базисом . Пусть - билинейная функция. Ее значения на базисных матрицах таковы: .

(В примере 2 доказано, что является скалярным произведением в ). Найти матрицу

Грама, координатную и векторно-матричную запись скалярного произведения в указанном базисе пространства .

Решение.

- скалярное произведение в .

, , .

- матрица Грама в базисе .

Пусть - произвольные матрицы из .

.

- вектор строка, - вектор столбец из координат матриц в базисе .

- векторно-матричная запись скалярного произведения в базисе .

.

. - координатная запись скалярного произведения в базисе .

Пример 6.

У трехмерного евклидова пространства в базисе матрица Грама равна

. Найти матрицу Грама в новом базисе , если

.

Решение.

, где .

В базисе скалярное произведение векторов , вычисляется по формуле

.

Следовательно,

,

,

,

,

,

.

.

Приведем еще одно решение задачи, основанное на формуле (2).

- матрица перехода от базиса к базису .

.

11.3. Пусть - евклидово пространство со скалярным произведением .

Определение. Векторы называются ортогональными, если .

Если - система из ортогональных векторов (т.е. при ), то эта система линейно независима.

Базис пространства , составленный из ортогональных векторов, называется ортогональным базисом. Если в ортогональном базисе все векторы имеют длину, равную 1, то такой базис называется ортонормированным.

Матрица Грама в ортогональном базисе - диагональная матрица с положительными элементами на главной диагонали. Матрица Грама в ортонормированном базисе -

единичная матрица.

Пример 7. У двумерного евклидова пространства в базисе матрица Грама равна . Найти ортогональный и ортонормированный базисы этого пространства и матрицы Грама в этих базисах.

Решение.

В базисе скалярное произведение векторов , вычисляется по формуле

.

Найдем ортогональный базис . В качестве первого вектора ортогонального базиса возьмем вектор . Второй вектор найдем из условия ортогональности векторов.

. Любое ненулевое решение полученного уравнения дает искомый вектор. Для определенности положим и найдем .

Следовательно, и - ортогональные векторы.