Занятие 11 (АиГ1)

Занятие 11. Поверхности второго порядка.

11.1. Канонические уравнения эллипсоида, конуса, гиперболоидов, параболоидов, цилиндров.

11.2. Построение графиков поверхностей второго порядка по их сечениям плоскостями, параллельными координатным плоскостям.

11.3. Построение графиков объемных тел, образованных поверхностями второго порядка и плоскостями.

Поверхностями второго порядка в пространстве называются поверхности, неявное задание которых имеет вид:

, (0)

где - заданные вещественные числа, - координаты точек поверхности. Наиболее важными и часто встречающимися поверхностями второго порядка являются: эллипсоид; гиперболоиды (однополостный, двуполостный); конус; параболоиды (эллиптический, гиперболический); цилиндры.

1. Эллипсоид. Каноническое уравнение эллипсоида:

. (1)

График эллипсоида приведен на рис. 1.

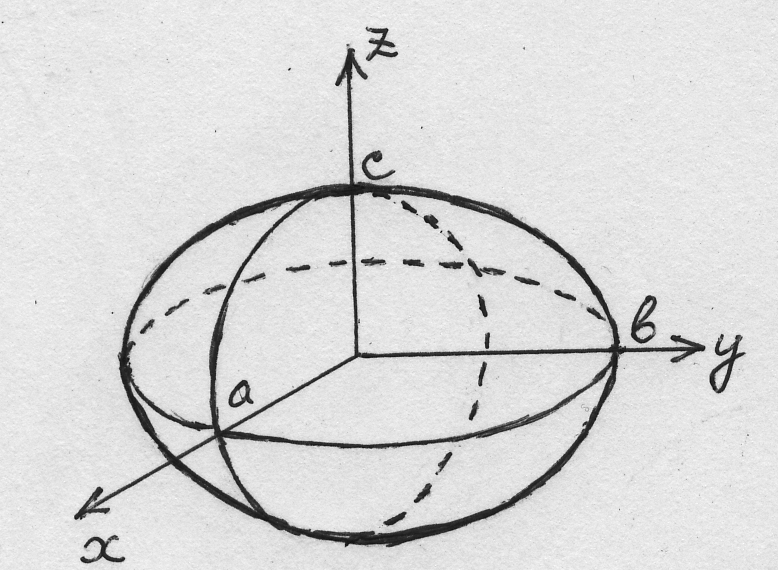
Рис. 1.

Эллипсоид (1) – замкнутая ограниченная поверхность, симметричная относительно начала координат , координатных осей и координатных плоскостей .

Пересечение эллипсоида (1) плоскостью дает эллипс .

Пересечение эллипсоида (1) плоскостью дает эллипс .

Пересечение эллипсоида (1) плоскостью дает эллипс .

Точка называется центром эллипсоида (1).

Если эллипсоид (1) "параллельно самому себе" сдвинут так, что центр эллипсоида попадет в точку , то уравнение полученного эллипсоида имеет вид: .

2. Однополостный гиперболоид. Его каноническое уравнение:

. (2)

График однополостного гиперболоида приведен на рис. 2.

Рис. 2.

Гиперболоид (2) - неограниченная поверхность, симметричная относительно начала координат , координатных осей и координатных плоскостей .

Пересечение гиперболоида (2) плоскостью дает эллипс .

Пересечение гиперболоида (2) плоскостью дает гиперболу .

Пересечение гиперболоида (2) плоскостью дает гиперболу .

Точка называется центром однополостного гиперболоида (2).

Если гиперболоид (2) "параллельно самому себе" сдвинут так, что центр гиперболоида попадет в точку , то уравнение полученного однополостного гиперболоида имеет вид: .

3. Двуполостный гиперболоид. Его каноническое уравнение:

. (3)

График двуполостного гиперболоида приведен на рис. 3.

Рис. 3.

Гиперболоид (3) - поверхность, представленная двумя раздельными неограниченными кусками поверхностей. Гиперболоид (3) симметричен относительно начала координат , координатных осей и координатных плоскостей .

Пересечение гиперболоида (3) плоскостью приводит к уравнению , которому не удовлетворяет ни одна точка на плоскости , т.е. гиперболоид (3) и плоскость не пересекаются.

Пересечение гиперболоида (3) плоскостью дает гиперболу .

Пересечение гиперболоида (3) плоскостью дает гиперболу .

Точка называется центром двуполостного гиперболоида (3).

Если гиперболоид (3) "параллельно самому себе" сдвинут так, что центр гиперболоида попадет в точку , то уравнение полученного двуполостного гиперболоида имеет вид: .

4. Конус. Его каноническое уравнение:

. (4)

График конуса приведен на рис. 4.

Рис. 4.

Конус (4) представлен двумя неограниченными кусками поверхностей, соединяющихся в начале координат . Конус (4) симметричен относительно начала координат , координатных осей и координатных плоскостей .

Пересечение конуса (4) плоскостью проводит к уравнению , решением которого служит одна точка , т.е. конус (4) пересекается плоскостью только в одной точке – начале координат.

Пересечение конуса (4) плоскостью приводит к уравнению , решением которого являются точки на двух прямых: .

Пересечение конуса (4) плоскостью приводит к уравнению , решением которого являются точки на двух прямых: .

Точка называется вершиной конуса (4).

Если конус (4) "параллельно самому себе" сдвинут так, что вершина конуса попадет в точку , то уравнение полученного конуса имеет вид: .

5. Эллиптический параболоид. Каноническое уравнение:

а) ; б) . (5)

Графики эллиптического параболоида для случаев а), б) приведены на рис. 5.

Рис. 5.

Эллиптические параболоиды (5) симметричны только относительно двух координатных плоскостей .

Пересечение параболоида плоскостью имеет одну точку . Пересечение параболоида плоскостью дает параболу .

Пересечение параболоида плоскостью дает параболу .

Аналогично определяются точки и линии пересечения параболоида плоскостями .

Точка является вершиной параболоидов (5).

Уравнения параболоидов (5) с вершиной в точке имеет соответственно вид: а) ; б) .

6. Гиперболический параболоид. Каноническое уравнение:

а) ; б) . (6)

Графики гиперболического параболоида для случаев а), б) приведены на рис. 6.

Рис. 6.

Гиперболические параболоиды (6) симметричны только относительно двух координатных плоскостей .

Пересечение параболоида плоскостью происходит по двум

прямым: .

Пересечение параболоида плоскостью дает параболу .

Пересечение параболоида плоскостью дает параболу .

Аналогично определяются линии пересечения параболоида плоскостями .

Точка называется вершиной параболоидов (6).

Уравнения параболоидов (6) с вершиной в точке имеет соответственно вид: а) ; б) .

7. Цилиндры.

7.1. Цилиндры второго порядка, параллельные оси , задаются уравнением (0), в котором отсутствует координата . Например,

а) - эллиптический цилиндр. Его график представлен на рис. 7.а.

б) - гиперболический цилиндр. Его график изображен на рис. 7.б.

а) б)

Рис. 7.

7.2. Цилиндры второго порядка, параллельные оси , задаются уравнением (0), в котором отсутствует координата .

7.3. Цилиндры второго порядка, параллельные оси , задаются уравнением (0), в котором отсутствует координата .

Основное внимание при изучении поверхностей второго порядка следует уделить нахождению линий пересечения поверхностей с плоскостями и выработке навыков построения графиков этих поверхностей по их сечениям плоскостями.

Приведем примеры на эту тему.

Пример 1. Привести к каноническому виду уравнение поверхности второго порядка . Дать ее название. Найти линии пересечения этой поверхности плоскостями и .

Решение.

1) - каноническое уравнение двуполостного гиперболоида, у которого .

2) Пересечением гиперболоида плоскостью (это – плоскость ) является гипербола .

3) Пересечение гиперболоида плоскостью (это – плоскость, проходящая через точку параллельно плоскости ) приводит к уравнению . Отсюда видно, что плоскость пересекается с гиперболоидом только при . Линией пересечения служит окружность с центром в точке и радиусом . Отметим, что растет вместе с ростом . Таким образом, заданный двуполостный гиперболоид является поверхностью вращения вокруг оси .

В соответствии с найденными сечениями нетрудно построить приходим график заданной поверхности.

Пример 2. Привести к каноническому виду уравнение поверхности второго порядка . Дать ее название. Найти линии пересечения этой поверхности плоскостями и , и с их помощью построить график этой поверхности.

Решение.

1) - каноническое уравнение конуса с вершиной в начале координат. Ось проходит внутри конуса. .

2) Пересечением конуса с плоскостью (это – плоскость ) служит пара прямых: .

3) Пересечение конуса с плоскостью (эта плоскость проходит через точку параллельно плоскости ) дает окружность: с центром в точке и радиусом .

Следовательно, данный конус – конус вращения вокруг оси .

В соответствии с проведенным исследованием строим график этого конуса (рис. 8).

Рис. 8.

_______________________________________________________________________

Домашнее задание.

1. Записать канонические уравнения эллипсоида, однополостного и двуполостного гиперболоидов, конуса, эллиптического и гиперболического параболоидов и привести их графики.

1. Найти линии пересечения поверхности второго порядка координатными плоскостями. Затем, с помощью найденных сечений построить график этой поверхности. Привести название поверхности.

2. Найти линии пересечения поверхности второго порядка координатными плоскостями. Затем, с помощью найденных сечений построить график этой поверхности. Привести название поверхности.

3. Найти линии пересечения поверхности второго порядка плоскостями: ; ; . С помощью найденных сечений построить график этой поверхности. Привести название поверхности.