
Занятие 12(Фдз 13)
.doc
Занятие 12 (Фдз 13).
Ортогональный и ортонормированный базисы. Метод ортогонализации базиса.
Ортогональные матрицы.
12.1. Ортогональные векторы. Ортогональный базис. Ортонормированный базис.
12.2. Метод ортогонализации базиса.
12.3. Ортогональные матрицы и их свойства.
12.1.
Пусть
![]() -
-
![]() -
мерное евклидово пространство,
-
мерное евклидово пространство,
![]() - скалярное произведение векторов.
Векторы
- скалярное произведение векторов.
Векторы
![]() называются ортогональными,
если
называются ортогональными,
если
![]() =0.
Система
=0.
Система
![]() из ортогональных векторов, т.е.
из ортогональных векторов, т.е.
![]() ,
всегда линейно независима.
,
всегда линейно независима.
Базис
![]() называется ортогональным, если он
состоит из ортогональных векторов.
называется ортогональным, если он
состоит из ортогональных векторов.
Базис
![]() называется ортонормированным, если
этот базис является ортогональным, и
все его векторы имеют длину, равную 1.
называется ортонормированным, если
этот базис является ортогональным, и
все его векторы имеют длину, равную 1.
Пример 1.
В базисе
![]() двумерного евклидова векторного
пространства
двумерного евклидова векторного
пространства
![]() матрица
матрица
![]() Грама имеет вид
Грама имеет вид
![]() .
Даны векторы
.
Даны векторы
![]() в базисе
в базисе
![]() .
Требуется найти, при каком значении
параметра
.
Требуется найти, при каком значении
параметра
![]() векторы
векторы
![]() будут ортогональными.
будут ортогональными.
Решение.
Скалярное
произведение
![]() векторов
векторов
![]() в базисе
в базисе
![]() задается формулой
задается формулой
 ,
где
,
где
![]() - координаты векторов
- координаты векторов
![]() в базисе
в базисе
![]() .
Следовательно,
.
Следовательно,
 .
.
Согласно определению
![]() будут ортогональными, если
будут ортогональными, если
![]() .
.
![]() .
.
12.2.
Пусть
![]() -
-
![]() -
мерное евклидово пространство,
-
мерное евклидово пространство,
![]() - скалярное произведение векторов
- скалярное произведение векторов
![]() .
Нахождение ортогонального и
ортонормированного базисов этого
пространства является одной из главных
задач. Решить эту задачу можно так.
.
Нахождение ортогонального и
ортонормированного базисов этого
пространства является одной из главных
задач. Решить эту задачу можно так.
Возьмем произвольный
базис
![]() пространства
пространства
![]() .
На его основе можно построить ортогональный
базис
.
На его основе можно построить ортогональный
базис
![]() пространства
пространства
![]() ,
если последовательно найти векторы
,
если последовательно найти векторы
![]() по следующему алгоритму:
по следующему алгоритму:
![]() ;
;
![]() ,
где
,
где
 ;
;
![]() ,
где
,
где
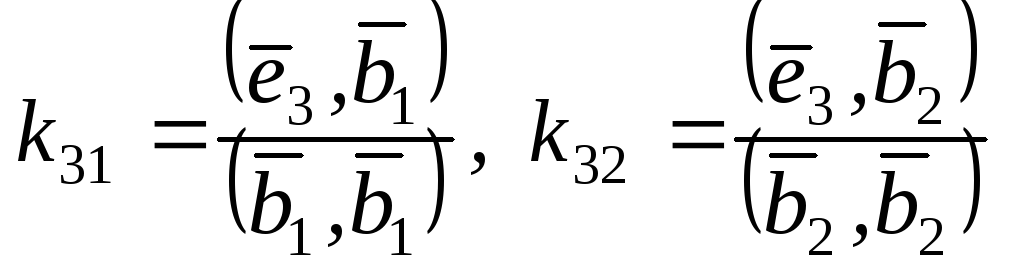 ;
(1)
;
(1)
………………………………………………………..
![]() ,
где
,
где
 .
.
Приведенный алгоритм называется методом ортогонализации базиса.
Теперь, используя
ортогональный базис
![]() легко находится ортонормированный
базис
легко находится ортонормированный
базис
![]() ,
в котором
,
в котором
![]() ,
,
![]() .
(2)
.
(2)
Переход от
![]() к
к
![]() по формулам (2) называется нормировкой
векторов
по формулам (2) называется нормировкой
векторов
![]() .
.
Пример 2.
Пусть
![]() - трехмерное евклидово пространство со
стандартным скалярным произведением
- трехмерное евклидово пространство со
стандартным скалярным произведением
![]() .
В этом пространстве задан базис
.
В этом пространстве задан базис
![]() .
Требуется ортогонализовать и
ортонормировать этот базис.
.
Требуется ортогонализовать и
ортонормировать этот базис.
Решение.
Проведем
ортогонализацию базиса
![]() .
Сделаем это с помощью формул (1).
.
Сделаем это с помощью формул (1).
![]() .
.
![]() ,
где
,
где
 .
.
![]() .
.
![]() .
.
![]() ,
где
,
где
 .
.
![]() .
.
![]()
![]()
Итак, получили:
![]() ,
,
![]() ,
,
![]() .
.
Проведем проверку ортогональности полученных векторов.
![]() ,
,
![]() ,
,
![]() .
.
Таким образом,
проверкой окончательно установлено,
что
![]() - ортогональный базис.
- ортогональный базис.
Чтобы найти
ортонормированный базис, надо
пронормировать векторы
![]() .
.
![]() .
.
![]() .
.
![]()
![]() .
.
Итог:
![]() ,
,
![]() ,
,
![]() -
-
ортонормированный базис.
В заключение
отметим, что базис, в котором задано
стандартное скалярное произведение,
также является ортонормированным, он
состоит из векторов
![]() .
.
Пример 3.
Рассмотрим двумерное евклидово
пространство

с базисом
 и скалярным произведением
и скалярным произведением
![]() ,
где
,
где
![]() - симметричная
билинейная функция. Ее значения на
базисных матрицах таковы:
- симметричная
билинейная функция. Ее значения на
базисных матрицах таковы:
![]() .
.
(См. пример 9 занятия 10 и пример 3 занятия 11).
Требуется ортогонализовать и ортонормировать этот базис.
Решение. Сначала
методом ортогонализации из
![]() получим ортогональный базис
получим ортогональный базис
![]() .
.
 .
.
![]() ,
где
,
где

 .
.
 ,
,
 - ортогональный базис.
- ортогональный базис.
Чтобы получить
ортонормированный базис
![]() ,
,![]() пронормируем матрицы
пронормируем матрицы
![]() .
.
 .
.
![]()
![]() .
.
 .
.
Ответ.
 ,
,
 - ортонормированный базис.
- ортонормированный базис.
Пример 4.
Рассмотрим трехмерное евклидово
пространство
![]() многочленов степени не выше второй
степени со стандартным базисом
многочленов степени не выше второй
степени со стандартным базисом
![]() и скалярным произведением
и скалярным произведением
![]() ,
где
,
где
![]() - симметричная билинейная функция со
следующими значениями на базисных
многочленах:
- симметричная билинейная функция со
следующими значениями на базисных
многочленах:
![]() .
.
(См. пример 8 занятия 10 и пример 2 занятия 11).
Исходя из базиса
![]() найти ортонормированный базис.
найти ортонормированный базис.
Решение.
Сначала методом
ортогонализации из
![]() получим ортогональный базис
получим ортогональный базис
![]() .
.
![]() .
.
![]() ,
где
,
где
 .
.
![]() ,
где
,
где
 .
.
 .
.

![]() .
.
![]() .
.
Итог:
![]() ,
,
![]() ,
,
![]() - ортогональный базис пространства
- ортогональный базис пространства
![]() .
.
Теперь из базиса
![]() получим ортонормированный базис
получим ортонормированный базис
![]() .
.
![]() .
.
![]() (см. вычисление
знаменателя у коэффициента
(см. вычисление
знаменателя у коэффициента
![]() ).
).
![]() .
.
![]()
![]()
![]()
![]() .
.
![]() .
.
Ответ.
![]() ,
,![]() ,
,![]() - ортонормированный базис.
- ортонормированный базис.
12.3.
Ортогональная
матрица –
матрица
![]() перехода от одного ортонормированного
базиса к другому ортонормированному
базису евклидова пространства
перехода от одного ортонормированного
базиса к другому ортонормированному
базису евклидова пространства
![]() .
.
Пусть
![]() и
и
![]() - ортонормированные базисы
- ортонормированные базисы
![]() -мерного
евклидова пространства
-мерного
евклидова пространства
![]() .
.
 ,
где
,
где
 .
.
![]() - ортогональная
матрица.
- ортогональная
матрица.
Свойство (необходимое
и достаточное условие) ортогональной
матрицы:![]() или
или
![]() ,
где
,
где
![]() - единичная матрица.
- единичная матрица.
Из этого свойства
выводится, что
![]() равен 1 или -1. Поэтому, ортогональные
матрицы составляют два класса. Для
одного класса ортогональных матриц
равен 1 или -1. Поэтому, ортогональные
матрицы составляют два класса. Для
одного класса ортогональных матриц
![]() ,
для другого
,
для другого
![]() .
.
Пример 5.
Даны матрицы
 .
.
Доказать, что
![]() - ортогональные матрицы.
- ортогональные матрицы.
Решение.
1.
 .
.
 .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

![]() - ортогональная
матрица. Легко проверяется, что
- ортогональная
матрица. Легко проверяется, что
![]()
2.
 .
.
 .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

![]() - ортогональная
матрица.
- ортогональная
матрица.
![]()
Пример 6.
Найти матрицу
![]() перехода от ортонормированного базиса
перехода от ортонормированного базиса
![]() к ортонормированному базису
к ортонормированному базису
![]() ,
,
![]() ,
,
![]()
трехмерного
евклидова пространства
![]() со стандартным скалярным произведением
со стандартным скалярным произведением
![]() и проверить, что эта матрица является
ортогональной.
и проверить, что эта матрица является
ортогональной.
Решение.
![]() .
.
![]() .
.
![]() .
.
 - матрица перехода
от базиса
- матрица перехода
от базиса
![]() к базису
к базису
![]() ,
,![]() ,
,![]() .
.
 .
.
![]() - ортогональная
матрица.
- ортогональная
матрица.
_________________________________________________________________________________
Домашнее задание.
1. В трехмерном
евклидовом пространстве
![]() со
стандартным скалярным произведением
со
стандартным скалярным произведением
![]() задан базис
задан базис
![]() .
Провести ортогонализацию этого базиса.
Затем, по полученному ортогональному
базису найти ортонормированный базис.
.
Провести ортогонализацию этого базиса.
Затем, по полученному ортогональному
базису найти ортонормированный базис.
2. Дано трехмерное
евклидово пространство
![]() ,
у которого матрица
,
у которого матрица
![]() Грама в базисе
Грама в базисе
![]() имеет вид
имеет вид
 .
.
![]() -новый базис пространства
-новый базис пространства
![]() ,
,
![]() .
Провести ортогонализацию базиса
.
Провести ортогонализацию базиса
![]() .
Затем, по полученному ортогональному
базису найти ортонормированный базис.
.
Затем, по полученному ортогональному
базису найти ортонормированный базис.
