
- •Distribution Overview
- •Discrete Distributions
- •Continuous Distributions
- •Probability Theory
- •Random Variables
- •Transformations
- •Expectation
- •Variance
- •Inequalities
- •Distribution Relationships
- •Probability and Moment Generating Functions
- •Multivariate Distributions
- •Standard Bivariate Normal
- •Bivariate Normal
- •Multivariate Normal
- •Convergence
- •Statistical Inference
- •Point Estimation
- •Empirical distribution
- •Statistical Functionals
- •Parametric Inference
- •Method of Moments
- •Maximum Likelihood
- •Delta Method
- •Multiparameter Models
- •Multiparameter delta method
- •Parametric Bootstrap
- •Hypothesis Testing
- •Bayesian Inference
- •Credible Intervals
- •Function of parameters
- •Priors
- •Conjugate Priors
- •Bayesian Testing
- •Exponential Family
- •Sampling Methods
- •The Bootstrap
- •Rejection Sampling
- •Importance Sampling
- •Decision Theory
- •Risk
- •Admissibility
- •Bayes Rule
- •Minimax Rules
- •Linear Regression
- •Simple Linear Regression
- •Prediction
- •Multiple Regression
- •Model Selection
- •Non-parametric Function Estimation
- •Density Estimation
- •Histograms
- •Kernel Density Estimator (KDE)
- •Smoothing Using Orthogonal Functions
- •Stochastic Processes
- •Markov Chains
- •Poisson Processes
- •Time Series
- •Stationary Time Series
- •Estimation of Correlation
- •Detrending
- •ARIMA models
- •Causality and Invertibility
- •Spectral Analysis
- •Math
- •Gamma Function
- •Beta Function
- •Series
- •Combinatorics

Amplitude A
Phase
U1 = A cos and U2 = A sin often normally distributed rv's
Periodic mixture
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
xt = |
|
(Uk1 cos(2 !kt) + Uk2 sin(2 !kt)) |
||||||
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
for k = 1; : : : ; q, are independent zero-mean rv's with variances 2 |
|||||||||
Uk1; Uk2, q |
2 cos(2 ! h) |
|
|
k |
||||||||
|
|
|
P t |
|
|
|
||||||
|
|
k |
|
k=1 |
k |
|
|
|
||||
(h) = |
k=1 |
|
q |
k |
|
|
|
|||||
|
(0) = E x2 |
= |
|
|
2 |
|
|
|
||||
Spectral |
representation of a periodic process |
|||||||||||
|
|
|
P |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(h) = 2 cos(2 !0h) |
||||||
|
|
|
|
|
|
|
2 |
2 |
||||
|
|
|
|
|
|
|
= |
|
e 2 i!0h |
+ |
|
e2 i!0h |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
2 |
|
||
Z1=2
=e2 i!h dF (!)
1=2
Spectral distribution function |
8 2 |
|
|
!0< !0 |
|
|
|
|||||
F (!) = |
=2 ! |
|
|
|
||||||||
|
> |
0 |
|
! < |
! |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
< |
|
! |
|
!0 |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
F (1) = F ( 1=2) = 0 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (1) = F (1=2) = (0) |
|
|
|
|
|
|
|
|
|
|
|
|
Spectral density |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
||||
X |
(h)e 2 i!h |
|
|
! |
|
|
||||||
f(!) = |
2 |
2 |
|
|||||||||
h=1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1=2 |
|
|
2 i!h |
f(!) d! h = 0; 1; : : : |
||
Needs Ph=1 j (h)j < 1 =) |
(h) = R 1=2 e |
|
||||||||||
f(!) 0
f(!) = f( !)f(!) = f(1 !)
R 1=2
(0) = V [xt] = 1=2 f(!) d!
White noise: fw(!) = w2
ARMA (p; q) ; (B)xt = (B)wt:
|
f |
x |
(!) = 2 |
j (e 2 i!)j2 |
|
|
|
w j (e 2 i!)j2 |
|
||
p |
|
|
|
q |
kzk |
where (z) = 1 Pk=1 |
kzk and (z) = 1 + Pk=1 |
||||
Discrete Fourier Transform (DFT)
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Xi |
|
|
|
|
|
|
|
|
d(!j) = n 1=2 |
xte 2 i!jt |
|
|||
|
|
|
|
|
=1 |
|
|
|
|
Fourier/Fundamental frequencies |
|
|
|
|
|
||||
|
|
|
|
!j |
= j=n |
|
|
||
Inverse DFT |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Xj |
|
|
|
|
|
|
|
|
|
xt = n 1=2 |
d(!j)e2 i!jt |
|
|||
|
|
|
|
|
=0 |
|
|
|
|
Periodogram |
|
|
|
I(j=n) = jd(j=n)j2 |
|
|
|||
Scaled Periodogram |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
P (j=n) = |
4 |
I(j=n) |
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
n |
|
|
|
|
|
|
||
|
2 |
n |
2 |
2 |
n |
2 |
|||
|
|
|
|||||||
|
|
|
|
X |
|
|
|
Xt |
|
|
|
|
|
|
+ n |
|
|||
= |
|
|
n t=1 xt cos(2 tj=n! |
=1 xt sin(2 tj=n! |
|
||||
22 Math
22.1Gamma Function
Z 1
Ordinary: (s) = ts 1e tdt
0
Z 1
Upper incomplete: (s; x) = ts 1e tdt
x
Z x
Lower incomplete: (s; x) = ts 1e tdt
0
( + 1) = ( ) |
> 1 |
||
(n) = (n 1)! |
n 2 N |
||
p |
|
|
|
(1=2) = |
|
||
22.2Beta Function
Ordinary: B(x; y) = B(y; x) = |
Z0 |
1 |
|
|
|
|
|
|
|
|
|||||
tx 1(1 t)y 1 dt = (x + y) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) (y) |
||
Incomplete: B(x; a; b) = Z0x ta 1(1 t)b 1 dt |
|
|
|
|
|
||||||||||
Regularized incomplete: |
a+b 1 |
|
|
|
|
|
|
|
|
|
|||||
|
B(x; a; b) |
a;b |
|
|
|
|
|
|
|
|
|
||||
I (a; b) = |
=2N |
Xj |
|
(a + b 1)! |
|
xj(1 |
|
x)a+b 1 j |
|||||||
|
|
|
|
|
|||||||||||
x |
B(a; b) |
|
|
j!(a + b |
|
1 |
|
j)! |
26 |
||||||
=a

I0(a; b) = 0 I1(a; b) = 1Ix(a; b) = 1 I1 x(b; a)
22.3Series
Finite
|
n |
|
|
|
|
+ 1) |
|
|
|
|
|
|
Xk = |
|
|
|
|
|
|
|
|||
|
n(n |
|
|
|
|
|
|||||
2 |
|
|
|
|
|
||||||
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
X(2k 1) = n2 |
|
|
|
|
|||||||
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
1)(2n + 1) |
||||
|
Xk2 |
|
|
|
|
|
|||||
|
= |
n(n + |
|
|
|
|
|||||
|
|
6 |
|
|
|||||||
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
+ 1) |
2 |
|||
k=1 k3 |
= n(n2 |
|
|
|
|||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
cn+1 1 |
|
|
|
||||
|
ck |
= |
|
c = 1 |
|||||||
|
kX |
|
|
c |
|
1 |
|
|
|
6 |
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
Binomial
|
n |
k |
= 2n |
|
|
|
|
|
|
k=0 |
|
|
|
|
|
||||
|
X |
n |
|
|
|
|
|
|
|
|
r k |
|
|
|
|
|
|
|
|
|
n |
= |
n |
|
|||||
k=0 |
|
||||||||
|
X |
+ k |
|
|
r + n + 1 |
|
|||
|
m |
= m + 1 |
|
|
|||||
|
n |
|
|
||||||
k=0 |
|
|
|||||||
|
X |
k |
|
|
n + 1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
Vandermonde's Identity: |
|
|||||||
|
k=0 |
k r k |
= |
r |
|||||
|
X |
m |
|
n |
|
|
|
m + n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
Binomial Theorem: |
|
|
||||||
|
k=0 |
k an kbk = (a + b)n |
|
||||||
|
X |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In nite
1
X
k=0
1
X
k=0
1
X
k=0
1
X
k=0
pk = 1 |
1 p |
1 |
pk = 1 p p jpj < 1 |
|
|
|||||||||||
; |
|
|
||||||||||||||
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
k=1 |
pk! |
|
|
|
|
|
|
|
|
|
|
|
|
d |
1 |
|
|
d 1 |
|
1 |
|
||||||
kpk 1 = |
|
|
= |
|
|
|
= |
|
jpj < 1 |
|||||||
dp |
k=0 |
dp |
1 p |
(1 p)2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r + k |
|
|
|
|
X |
|
|
|
|
|
|
|
|
|||
|
xk = (1 x) r r 2 N+ |
|
|
|||||||||||||
k |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
k pk = (1 + p) |
jpj < 1 ; 2 C |
|
|
22.4Combinatorics
Sampling
k out of n |
|
w/o replacement |
|
|
|
|
w/ replacement |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k 1 |
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|||
ordered |
|
Y |
|
|
|
|
|
|
|
|
|
|
nk |
|
|
|||
|
|
|
|
(n |
|
k)! |
|
|
|
|
||||||||
nk = |
(n i) = |
|
|
|
|
|
||||||||||||
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
unordered |
n |
|
= |
nk |
= |
|
|
n! |
|
|
|
|
|
n 1 + r |
= |
n 1 + r |
|
|
k |
|
k! |
k!(n k)! |
|
|
|||||||||||||
|
|
|
r |
|
n 1 |
|||||||||||||
Stirling numbers, 2nd kind |
|
|
|
|
|
|
|
|
|
|
(0 |
|
|
|||||||||
|
k |
|
|
|
|
k |
|
k |
1 |
|
|
|
0 |
|
else |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n = k n |
1 + n 1 |
|
1 k n |
n = 1 n = 0 |
|
||||||||||||||||
Partitions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn+k;k = |
Xi |
|
|
|
k > n : Pn;k = 0 |
n 1 : Pn;0 = 0; P0;0 = 1 |
||||||||||||||||
|
|
Pn;i |
|
|||||||||||||||||||
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Balls and Urns |
|
|
f : B ! U |
|
|
D = distinguishable, :D = indistinguishable. |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
jBj = n, jUj = m |
|
f arbitrary |
|
f injective |
f surjective |
f bijective |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 |
|
|
else |
m |
(0 |
else |
|||
B : D; U : D |
|
|
mn |
|
|
|
mn |
|
m |
n |
m! n |
n! m = n |
||||||||||
B : :D; U : D |
|
|
n |
|
|
|
|
n |
|
m |
|
1 |
(0 |
else |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
m = n |
||||
|
|
|
|
|
|
|
m + n 1 |
|
|
|
|
|
m |
|
n 1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
: |
|
|
|
m |
|
k |
|
|
|
(0 |
|
|
else |
|
m |
|
(0 |
else |
||
B : D; U : D |
|
k=1 |
|
|
|
1 m n |
|
|
1 |
m = n |
||||||||||||
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B : D; U : D |
|
m |
P |
|
|
|
|
1 m n |
P |
|
|
1 |
m = n |
|||||||||
|
X |
|
|
|
|
|
|
|||||||||||||||
: |
|
|
|
: |
|
|
|
n;k |
|
|
(0 |
|
|
else |
|
|
n;m |
(0 |
else |
|||
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
References
[1]P. G. Hoel, S. C. Port, and C. J. Stone. Introduction to Probability Theory. Brooks Cole, 1972.
[2]L. M. Leemis and J. T. McQueston. Univariate Distribution Relationships.
The American Statistician, 62(1):45{53, 2008.
[3]R. H. Shumway and D. S. Sto er. Time Series Analysis and Its Applications With R Examples. Springer, 2006.
[4]A. Steger. Diskrete Strukturen { Band 1: Kombinatorik, Graphentheorie, Algebra. Springer, 2001.
[5]A. Steger. Diskrete Strukturen { Band 2: Wahrscheinlichkeitstheorie und Statistik. Springer, 2002.
[6]L. Wasserman. All of Statistics: A Concise Course in Statistical Inference. Springer, 2003.
27
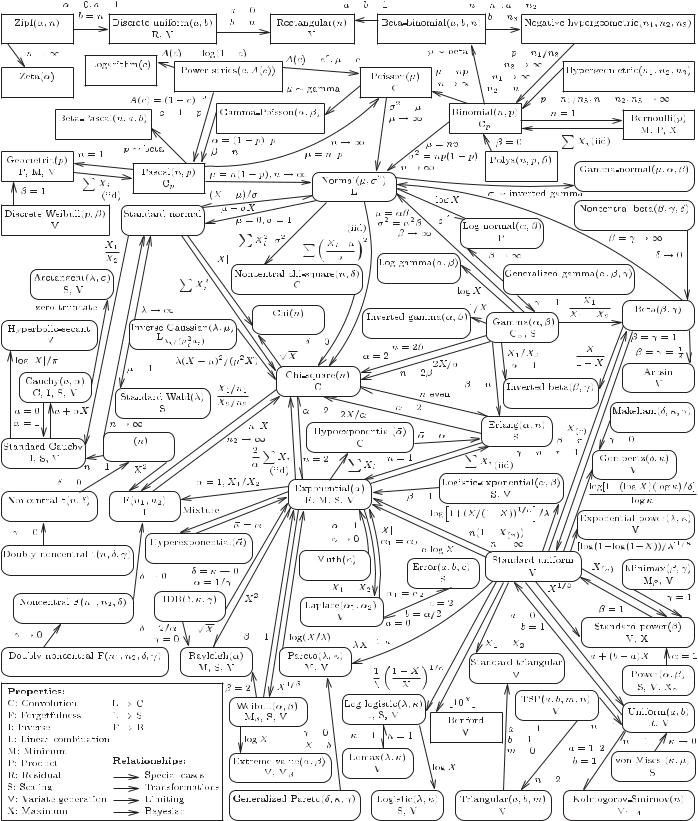
].  2
2
Univariate distribution relationships, courtesy Leemis and McQueston [
28
