IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функции. - М.: Наука, 1980. 248 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

Лабораторная работа № 11

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ

ПО ФОРМУЛЕ ТРАПЕЦИЙ

1. ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления интегралов с помощью квадратурных формул.

2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть требуется вычислить интеграл.

Разобьем отрезок с помощью равноотстоящих точек

на равных частей. Шаг .

Пусть=.

Заменяя функцию многочленом Лагранжа

где ,

получаем квадратурную формулу

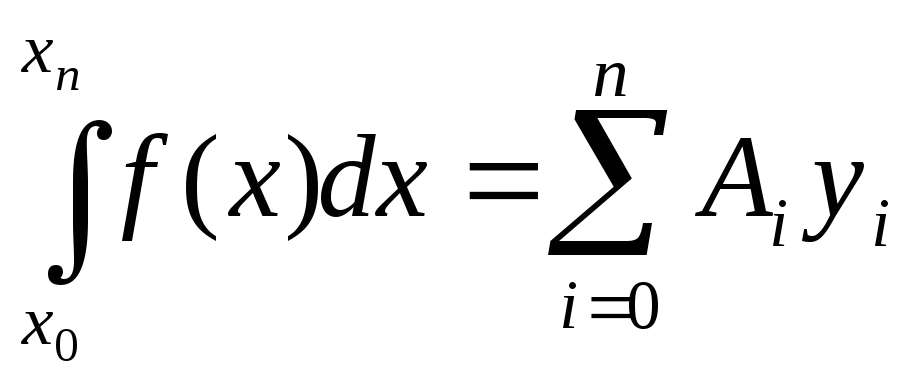. (1)

где

().

При этом .

Полагая , будем иметь

(2)

Тогда квадратурная формула (1) принимает вид

. (3)

Формулы (2) и (3) называются формулами Ньютона – Котеса.

Полагая в формуле (2) =1, находим

В результате получаем формулу трапеций

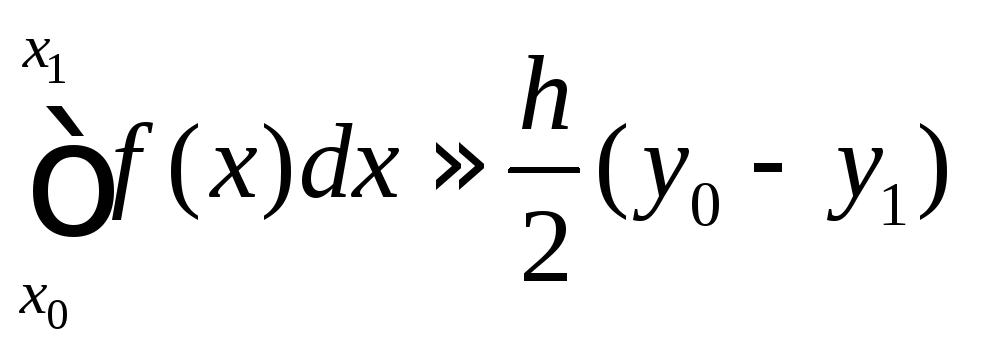. (4)

Для повышения точности на отрезке [a,b] вводится достаточно густая сетка

.

Интеграл разбивается на сумму интегралов по шагам сетки и к каждому шагу применяют формулу (4).

Обобщенная формула трапеций на равномерной сетке с шагом имеет вид

(5)

Для равномерной сетки справедлива следующая мажорантная оценка погрешности формулы трапеций:

где

3. ЗАДАНИЕ

Вычислить с помощью формулы трапеций определенный интеграл от заданной функции.

Варианты заданий

№	f(x)	Пределы интегрирования
		a	b
		0,1
			3
			13
			3,2
			3
			3
		0	1
		0	1
			3
		0
			4
		0

Здесь kпоследняя цифра номера группы.

Указание: При вычислении интеграла положить h=0.1

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

2. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

3. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа № 12

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ

ПО ФОРМУЛЕ СИМПСОНА

4. ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления интегралов с помощью квадратурных формул.

ΙΙ.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть требуется вычислить интеграл.

Разобьем отрезок с помощью равноотстоящих точек

на равных частей. Шаг .

Пусть=.

Полагая в формулах Ньютона – Котеса

;

, получаем

.

Так как , то

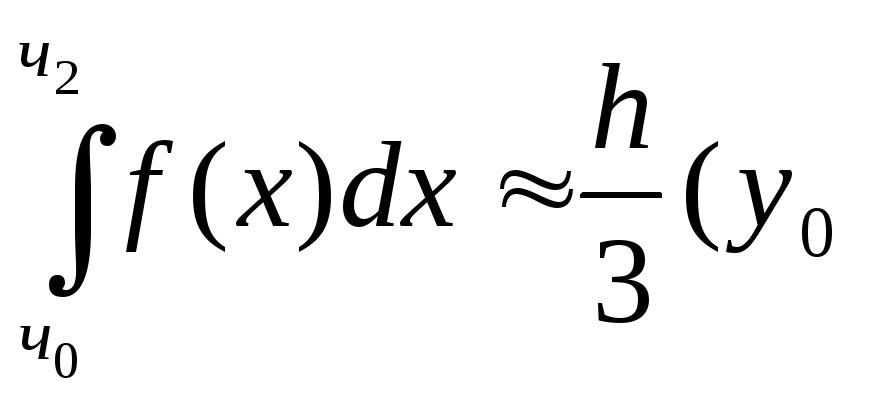
. (1)

Это формула Симпсона.

Для повышения точности отрезок [a,b] разбивается на четное число частей . Тогда

Интеграл разбивается на сумму интегралов. К каждому удвоенному промежутку длиныприменим формулу (1).

Получим обобщенную формулу Симпсона

. (2)

Для погрешности формулы Симпсона (2) справедлива оценка

где

IIΙ.ЗАДАНИЕ

Вычислить с помощью формулы Симпсона определенный интеграл от заданной функции. Варианты заданий приведены в лабораторной работе № 11.