4.3.3 Интерполяционный многочлен Лагранжа

Интерполяционный многочлен Лагранжа представляет собой линейную комбинацию

, (4.10)

где .

Выражение (3.10) есть многочлен степени не выше n. В узле этот многочлен принимает значение, так как

(i=0,1,…,n);

.

Учитывая, что

,

Можно рассмотреть его производную в точке :

и записать многочлен Лагранжа в виде

.

Величины являются как бы весовыми многочленами соответствующих узлов и называются множителями Лагранжа.

Интерполяционный многочлен Лагранжа для равноотстоящих узлов интерполяции (т.е. гдеh – шаг интерполяции) можно записать в виде

, (4.11)

где

; .

Пример 2.Функция y=sin(x) задана в виде таблицы (табл.3)

Таблица 3. Данные к примеру 2

x	0
y	0	0.707	1

Пользуясь интерполяционным многочленом Лагранжа, определить ее значение в точке . Оценить погрешность.

Прежде всего определим . Подставляя в формулу (4.11) полученное значение и значениеприn=2, имеем

Для оценки погрешности воспользуемся формулой (4.9). Тогда поэтому

.

При вычислении погрешности градусную меру следует перевести в радиальную.

Итак, получили .

Лекция № 11

4.3.4 Конечные разности

При построении интерполяционных многочленов на равномерной сетке используются величины, называемые конечными разностями.

Рассмотрим равномерную сетку с шагом h: , в узлах которой заданы значенияфункции.

В математической литературе используются три типа конечных разностей: нисходящие разности для интерполяции назад; центральные разности для построения центральных интерполяционных формул и восходящие разности для интерполяций вперед.

Конечной разностью первого порядка называется разность между значениями функции в данном и предыдущем узлах:

…… (4.12)

Это определение можно записать в другой форме:

; (4.13)

Конечной разностью второго порядка называется разность между значениями первой конечной разностью второго в данном и предыдущем узлах:

. (4.14)

Аналогичным образом определяются конечные разности произвольного порядка k:

(4.15)

В некоторых рассчитываемых ниже интерполяционных формулах наряду с разностями (4.15) используются средние арифметические соседних конечных разностей одного и того же порядка:

(4.16)

Первая из этих величин используется при нечетном k, а вторая – четном k.

Рассмотрим некоторые свойства конечных разностей.

1. Нисходящие, восходящие и центральные разности связанны между собой следующими соотношениями:

(4.17)

2. Конечная разность удовлетворяет равенству

, (4.18)

где а и b постоянные.

3. Конечная разность связана с соответствующей производной соотношением

(4.19)

4. Конечная разность порядка k может быть представлена в виде следующей линейной комбинации значений :

, (4.20)

где - число сочетаний из к элементов по j элементов (причем ).

Исходные значения функции , как правило, задаются с некоторой погрешностью, представляющей собой ошибки округления или случайные ошибки, поэтому целесообразно рассматривать влияние этих факторов на погрешности конечных разностей высших порядков.

Если значения заданы приближенно или же по каким-либо причинам вычисленные значения многочленане может быть произведено абсолютно точно, то фактически получается лишь приближенное значениедля точного. При этом вычислительная погрешность

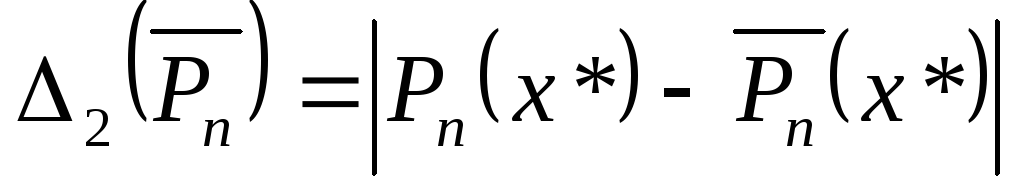
оценивается по общим правилам вычисления погрешности.

Рассмотрим многочлен Лагранжа . Пусть требуется вычислитьпри заданных значенияхи их погрешностях. Величины коэффициентов Лагранжапротабулированы для равностоящих узлов и их можно считать точными числами, поскольку они получены из точных значений узлов и точного х*. Поэтому для многочленов Лагранжа имеем:

.

В случае, когда все одинаковы и равны, получаем

.

Пример 3. На отрезке получить равномерную оценку вычислительной погрешности значений интерполяционного многочлена Лагранжа, построенного для функциипо узлам,,.

Так как , аесть точное число, то искомая вычислительная погрешность имеет вид

Нетрудно показать, что на данном отрезке принимает максимальное значение в точках, и по этому искомая оценка есть.