
- •Министерство образования и науки Российской Федерации
- •Оглавление
- •Лекция № 1
- •1. Особенности математических вычислений, реализуемых на эвм: теоретические основы численных методов: погрешности вычислений
- •1.1. Дискретизация
- •1.3. Погрешность
- •1.4. Устойчивость и сложность алгоритма (по памяти, по времени)
- •2.1. Основные понятия линейной алгебры. Классификация методов решения
- •2.2. Метод исключения Гаусса. Вычисление определителя и обратной матрицы методом исключения
- •2.3. Численные методы решения линейных уравнений
- •2.3.1. Метод прогонки
- •2.3.2. Итерационные методы
- •3.1. Решение нелинейных уравнений
- •3.1.1. Метод половинного деления
- •3.1.2. Метод простой итерации
- •3.1.3. Метод Ньютона
- •3.1.4. Метод секущих
- •3.1.5. Метод парабол
- •3.2. Методы решения нелинейных систем уравнений
- •4.1.Функция и способы ее задания
- •4.2 Основные понятия теории приближения функций
- •4.3 Интерполяция функций
- •4.3.1 Интерполирование с помощью многочленов
- •4.3.2 Погрешность интерполяционных методов
- •4.3.3 Интерполяционный многочлен Лагранжа
- •4.3.4 Конечные разности
- •4.3.5 Интерполяционные многочлены Стирлинга и Бесселя
- •4.3.6 Интерполяционные многочлены Ньютона
- •4.3.7 Разделенные разности
- •4.3.8 Интерполяционный многочлен Ньютона для произвольной сетки узлов
- •4.3.9 Итерационно-интерполяционный метод Эйткина
- •4.3.10 Интерполирование с кратными узлами
- •4.4 Равномерное приближение функций. Приближение методом наименьших квадратов
- •5.1. Численное дифференцирование
- •5.2. Формулы численного интегрирования
- •5.3. Решение обыкновенных дифференциальных уравнений. Метод конечных разностей для численного решения дифференциальных уравнений
- •Интегрирование дифференциальных уравнений с помощью степенных рядов
- •5.4. Преобразование Фурье
- •5.4.1 Применения преобразования Фурье
- •5.4.2 Разновидности преобразования Фурье Непрерывное преобразование Фурье
- •Ряды Фурье
- •Дискретное преобразование Фурье
- •Оконное преобразование Фурье
- •Другие варианты
- •5.4.3 Интерпретация в терминах времени и частоты
- •5.4.4 Таблица важных преобразований Фурье
- •Библиографический список
4.3 Интерполяция функций
4.3.1 Интерполирование с помощью многочленов
Рассмотрим задачу
интерполирования функции f
с помощью
алгебраических многочленов. В этом
случае аппроксимирующая функция
![]() имеет вид
имеет вид
![]() . (4.1)
. (4.1)
Выбор конкретного значения n во многом определяется свойствами аппроксимируемой функции, требуемой точностью, а также узлами интерполирования. На выбор величины n существенное влияние оказывает и вычислительный процесс, привносящий в результат дополнительную погрешность.
В качестве критерия
согласия принимается условие совпадения
![]() иf
в узловых
точках. Для однозначного определения
n+1
коэффициентов
иf
в узловых
точках. Для однозначного определения
n+1
коэффициентов
![]() многочлена
многочлена![]() необходимо потребовать совпаденияf
и
необходимо потребовать совпаденияf
и
![]() в (n+1)-й
узловой точке:
в (n+1)-й
узловой точке:
![]() (i
= 0,1,…,n) (4.2)
(i
= 0,1,…,n) (4.2)
Многочлен
![]() ,
удовлетворяющий условиям (3.2), называетсяинтерполяционным
многочленом. Чтобы
подчеркнуть зависимость этого многочлена
от функции f,
его часто обозначают
,
удовлетворяющий условиям (3.2), называетсяинтерполяционным
многочленом. Чтобы
подчеркнуть зависимость этого многочлена
от функции f,
его часто обозначают
![]() .
.
Под погрешностью
интерполяции
![]() в случае, когда необходимо вычислить
значение функцииf(x)
в одной точке
в случае, когда необходимо вычислить
значение функцииf(x)
в одной точке
![]() ,
понимают абсолютную величину разности
между точным и приближенным значениями:
,
понимают абсолютную величину разности
между точным и приближенным значениями:
![]() . (4.3)
. (4.3)
В том же случае,
когда интерполяция производится на
всем отрезке
![]() ,
в качестве погрешности принимается
максимальное отклонение многочлена
,
в качестве погрешности принимается
максимальное отклонение многочлена![]() от функцииf
на рассматриваемом отрезке:
от функцииf
на рассматриваемом отрезке:
![]() .
.
Итак, рассмотрим
следующую задачу интерполирования. На
сетке
![]() в узлах
в узлах![]() заданы значения
заданы значения![]() (i
= 0,1,….,n)
функции f.
Требуется построить интерполяционный
многочлен
(i
= 0,1,….,n)
функции f.
Требуется построить интерполяционный
многочлен
![]() ,
совпадающий сf
в узлах
,
совпадающий сf
в узлах
![]() ,
и оценить погрешность
,
и оценить погрешность![]() .
.
Теорема 1. Пусть:
на отрезке [a,b] заданна сетка
 ;
;заданны произвольные числа
 (i=0,1,…,n).
(i=0,1,…,n).
Тогда существует
единственный многочлен
![]() степени не вышеn,
принимающий в узлах
степени не вышеn,
принимающий в узлах
![]() заданные значения
заданные значения![]()
Из условий для
определения неизвестных коэффициентов
![]() многочлена
многочлена
![]() получаем систему алгебраических
уравнений
получаем систему алгебраических
уравнений
![]() (i=0.1,….,n) (4.4)
(i=0.1,….,n) (4.4)
Определитель этой системы
 (4.5)
(4.5)
есть определитель
Вандермонда, который отличен от нуля
при условии
![]() при
при![]() .
.
Коэффициенты
интерполяционного многочлена (4.1) можно
определить, положив в системе (4.4)
![]() и решив ее, например, по формуле Крамера:
и решив ее, например, по формуле Крамера:
![]() .
.
Здесь
![]() - определитель, получающийся изW
заменой столбца членов, содержащих
(n-k)-ю
степень
- определитель, получающийся изW
заменой столбца членов, содержащих
(n-k)-ю
степень
![]() (i=0,1,…,n),
на столбец
(i=0,1,…,n),
на столбец
![]() свободных членов системы (3.4)
свободных членов системы (3.4)
 . (4.7)
. (4.7)
Подставив полученные
значения коэффициентов в равенство
(4.1), приходим к новой форме представления
интерполяционного многочлена
![]() :
:
 (4.8)
(4.8)
На практике обычно используются интерполяционные многочлены первой и второй степеней. При этом говорят о линейной и квадратичной интерполяции.
Пример 1.
По узлам
![]() и соответствующим значениям функции
и соответствующим значениям функции![]() построить интерполяционный многочлен,
представив его в виде линейной комбинации
значений
построить интерполяционный многочлен,
представив его в виде линейной комбинации
значений![]() .
.
Согласно формуле (4.8) имеем

Разложив определитель по элементам 1-го столбца, получим

Учитывая, что
 ,
,
окончательно находим
![]()
4.3.2 Погрешность интерполяционных методов
Оценка меры погрешности, как правило, производится на для отдельно взятой функции, а для целого класса функций, обладающих определенными общими свойствами.
Если точка
интерполирования
![]() фиксирована, то за меру погрешности
естественно принять величину
фиксирована, то за меру погрешности
естественно принять величину![]() - остаточный член интерполяционной
формулы, зависящий от свойств функцииf,
параметров интерполирования и положения
точки интерполяции. Если же точка
- остаточный член интерполяционной
формулы, зависящий от свойств функцииf,
параметров интерполирования и положения
точки интерполяции. Если же точка
![]() заранее не известна, а интерполирование
осуществляется на отрезке
заранее не известна, а интерполирование
осуществляется на отрезке![]() ,
то за меру погрешности целесообразно
принять величину
,
то за меру погрешности целесообразно
принять величину
![]() .
.
Теорема 2. Пусть
узлы
 различны в месте
различны в месте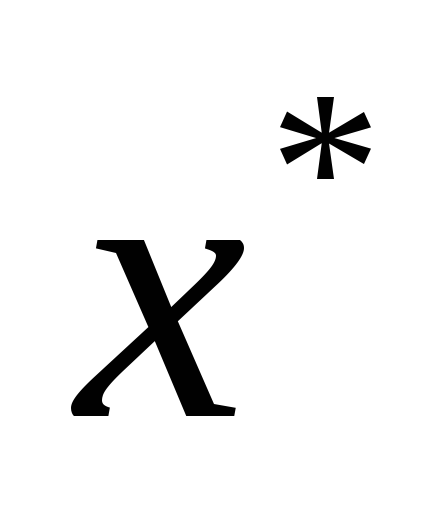 с принадлежат отрезку
с принадлежат отрезку ;
;функция f имеет на
 непрерывную производную порядкаn+1.
непрерывную производную порядкаn+1.
Тогда существует
такая точка
![]() ,
что
,
что
 .
.
Пусть для
определенности
![]() ;
;![]() .
Тогда равномерная на всем отрезке [a,b]
оценка для фиксированной сетки.
.
Тогда равномерная на всем отрезке [a,b]
оценка для фиксированной сетки.
![]() , (4.9)
, (4.9)
где
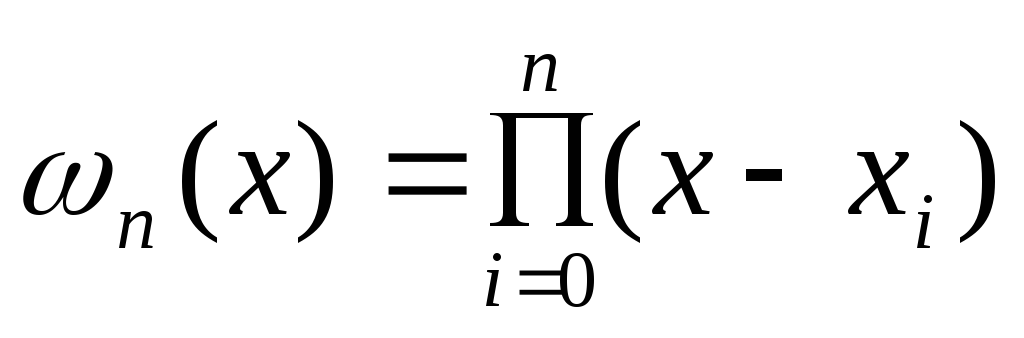 .
.
