Лекция 6

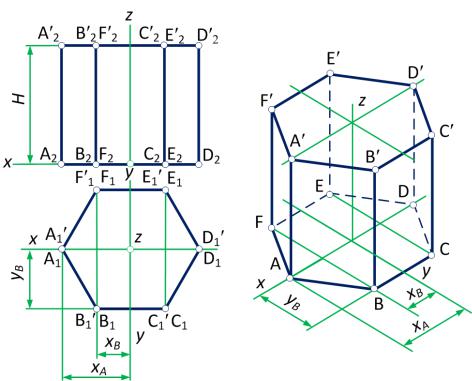
(рис.101, а), высота призмы Н. Через центр шестиугольника проведем оси координат х, у.

Построим в аксонометрии сначала шестиугольник основания призмы, для чего проведем аксонометрические оси х, у, z (рис. 101,б). По обе стороны от центра основания вдоль оси х отложим координаты точек А и D. По оси у отложим расстояния до середины сторон ВС и EF - координаты YF и YB и через полученные точки проведем прямые, параллельные оси х.

Рисунок 101

На этих прямых по обе стороны от оси у отложим половину длины сторон шестиугольника – координату ХВ. Получим проекции остальных вершин шестиугольника основания. Соединим полученные точки прямыми. Через вершины А, В, С, D, Е, F основания призмы проведем вертикальные прямые, равные высоте призмы (координата ZН). Соединив верхние концы этих высот, получим прямоугольную изометрию верхнего основания и всей призмы. Невидимые стороны нижнего основания и невидимые боковые ребра призмы выполняем штриховыми линиями.

Аксонометрия цилиндра (рис. 102)

Аксонометрические изображения цилиндра определяются

аксонометрическими изображениями окружностей его оснований. На рис.102 показано построение изометрической проекции цилиндра. На аксонометрической оси z откладываем высоту цилиндра Н, проводим линии, параллельные осям х и у. Строим изометрическую проекцию окружности верхнего основания (см. построение овала). Аналогичным образом выполняем построение изометрической проекции окружности нижнего основания. Проводим контурные образующие цилиндра.

Рисунок 102

Аксонометрия шара (рис. 103)

изобразятся тремя одинаковыми эллипсами (рис.103), в диметрии два эллипса одинаковы, третий близок к окружности. Внешний контур шара всегда является касательным ко всем трем эллипсам В аксонометрии полюсы шара — точки N и S не лежат на контуре видимости шара. Положение их определяется пересечением эллипсов, лежащих в вертикальных плоскостях.