Парная линейная регрессия (с демо)
.docПарная линейная регрессия
Предварительные расчеты:
;
;
;
;
;
;
.
Построение таблицы вида
|
|
x |
y |
xy |
|
|
|
………… |
………. |
……… |
…….. |
……… |
……… |
|
Среднее значение |
|
|
|
|
|
Формулы для расчетов параметров:
,
.
При компьютерном подборе использовать встроенную функцию Линейн
Оценка тесноты связи:
а) коэффициент
корреляции
,
или
;
При компьютерном подборе использовать встроенную функцию Коррел
б) коэффициент
эластичности
;
в) коэффициент
детерминации
.
Оценка значимости уравнения регрессии в целом:
Предварительные расчеты с построением таблицы вида
|
|
x |
y |
|
|
|
|
|
………… |
………. |
……… |
…….. |
……… |
……… |
|
а) F-критерий
Фишера при
числе степеней свободы
и
и уровне значимости 0,05 смотреть в
таблице. Расчетное значение критерия:
.
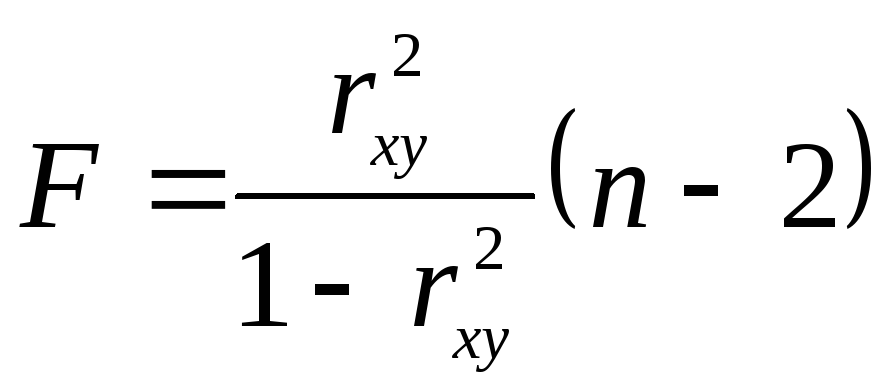Если расчетное значение F- критерия больше табличного, нулевая гипотеза об отсутствии значимой связи признаков x и y отклоняется, и делается вывод о существенности этой связи.
б) Средняя ошибка аппроксимации
.
Оценка значимости параметров регрессии:
а) Стандартная ошибка параметра a рассчитывается по формуле
,
где
.
б) Стандартная ошибка коэффициента регрессии b рассчитывается по формуле
.
в) Стандартная
ошибка коэффициента корреляции
рассчитывается по формуле
.
t-критерий
Стъюдента при числе степеней свободы
и уровне значимости 0,05 смотреть в
таблице.
Фактические значения t-статистики:
,
,
.
Если фактическое значение по абсолютной величине превышает табличное, гипотезу о несущественности параметра регрессии можно отклонить, параметр признается значимым.
Связь между F-критерием Фишера и t-критерием Стъюдента выражается равенством
.
Расчет доверительных интервалов для параметров регрессии:
Доверительный
интервал для параметра a
определяется
как
;
доверительный
интервал для коэффициента регрессии
определяется
как
.
При компьютерном анализе использовать в Excel Сервис/Анализ данных/Регрессия.
Интервальный прогноз на основе линейного уравнения регрессии:
Пусть
– прогнозное значение факторного
признака;
–
точечный прогноз результативного
признака. Тогда
а) средняя ошибка
прогноза
:
;
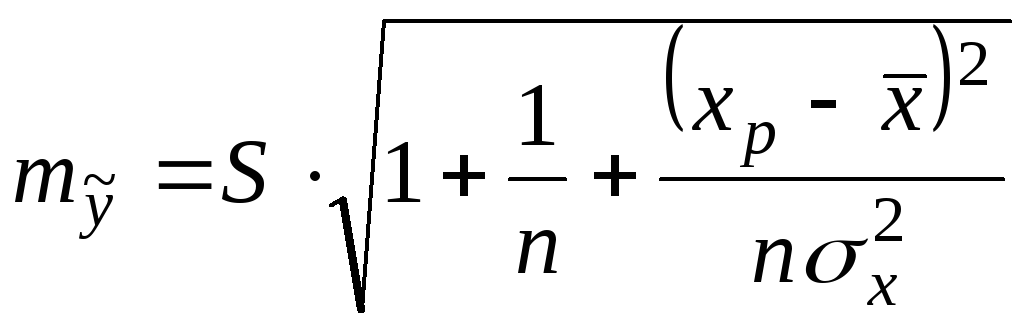б) доверительный интервал прогноза
.
Практические рекомендации по выполнению расчетов
с помощью табличного редактора MS Excel
Активизация надстройки Пакет анализа
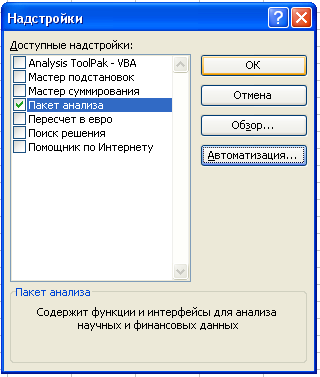
Для активизации надстройки Пакет анализа необходимо выполнить следующие действия:
1. Выбрать команду Сервис/Надстройки.
2. В появившемся диалоговом окне установить флажок Пакет анализа.
В соответствии с вариантом задания, используя статистический материал, необходимо:
1. Рассчитать
параметры уравнения линейной парной
регрессии
.
2. Оценить тесноту связи зависимой переменной (результативного фактора) с объясняющей переменной с помощью показателей корреляции и детерминации.
3. Оценить с помощью F-критерия Фишера статистическую надежность моделирования.
4. Оценить статистическую значимость параметров регрессии и корреляции.
5. Определить среднюю ошибку аппроксимации.
6. Используя коэффициент эластичности, выполнить количественную оценку влияния объясняющего фактора на результат.
7. Выполнить точечный и интервальный прогноз результативного признака при увеличении объясняющего признака на 25% от его среднего значения (достоверность прогноза 95%).
8. На одной диаграмме изобразить поле корреляции исходных данных и прямую регрессии.
Пример
Имеются данные о годовой цене программы «Мастер делового администрирования» и числе слушателей в образовательном учреждении.
|
Цена программы, тыс. долл., y |
8 |
5 |
4,9 |
4 |
3,8 |
3,5 |
3,8 |
3,7 |
3,6 |
3,5 |
3,4 |
3 |
3 |
|
Число слушателей, чел., x |
5 |
10 |
12 |
15 |
20 |
22 |
25 |
30 |
35 |
36 |
40 |
50 |
60 |
I. Вводим исходные данные в документ Excel.
II. Вызываем надстройку Анализ данных в меню Сервис.
III. Выбираем инструмент Регрессия.
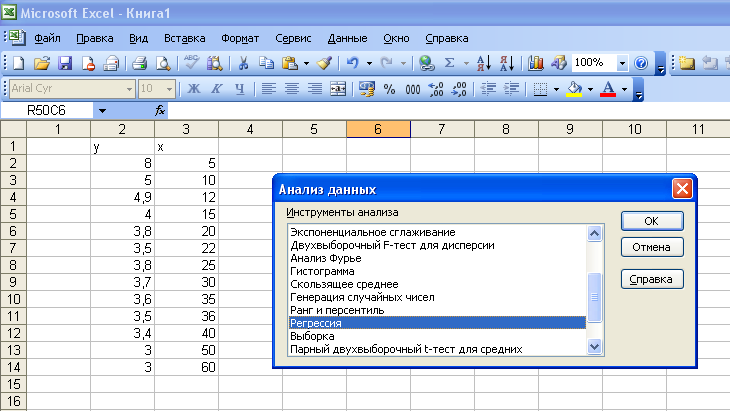
IV. Заполняем соответствующие позиции окна Регрессия.
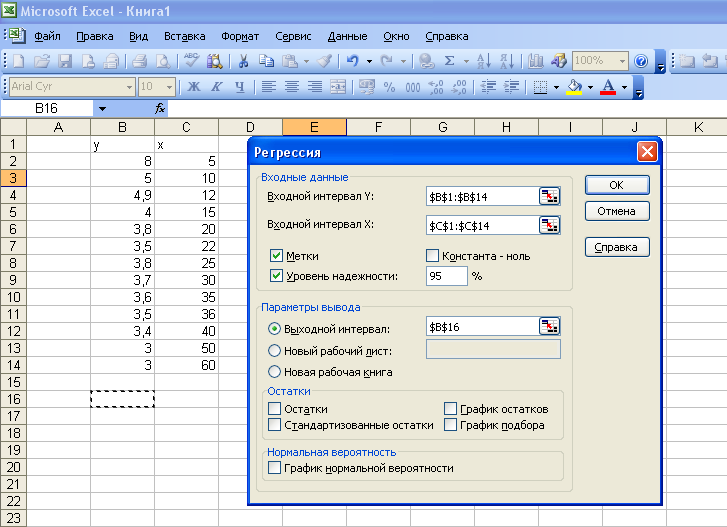
V. После нажатия Ок получаем протокол решения задачи.
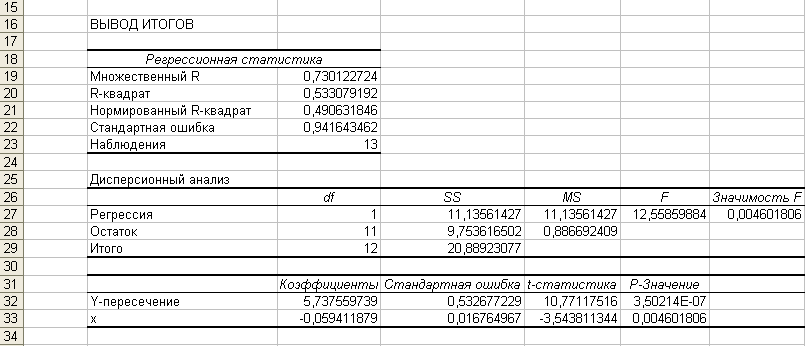
VI. Анализируем полученный протокол.
1) Коэффициент
регрессии
;
Свободный член
уравнения регрессии
.
Примечание. При необходимости результаты округляются с нужной точностью. Требование по округлению можно провести изначально, задав количество знаков после запятой в меню Формат ячейки.
Уравнение парной
линейной регрессии имеет вид:
.
2) Коэффициент
корреляции
,
что свидетельствует о тесной связи
признаков y
и x.
Коэффициент детерминации
.
Полученное уравнение регрессии объясняет
53% вариации признака y,
остальные 47% изменчивости этого признака
обусловлены влиянием неучтенных в
модели факторов.
3) Оценим статистическую
значимость (надежность моделирования)
уравнения в целом. Расчетное значение
критерия Фишера указано в протоколе,
.
Критическое значение этого критерия
можно найти с помощь статистической
функции FРАСПОБР
табличного
редактора Еxcel.
Входными параметрами этой функции являются:
– уровень значимости (вероятность), имеется в виду вероятность ошибки отвергнуть верную гипотезу о статистической незначимости построенного уравнения регрессии. Как правило, выбирают уровень значимости, равный 0,05 или 0,01;
– число степеней
свободы 1 – совпадает с количеством
параметров при переменной в уравнении
регрессии, для парной линейной регрессии
это число равно единице;
– число степеней
свободы 2 равно для парной линейной
регрессии
,
где n
– объем исходных статистических данных.
Выполняем действия Вставка/Функция, выбираем нужное.
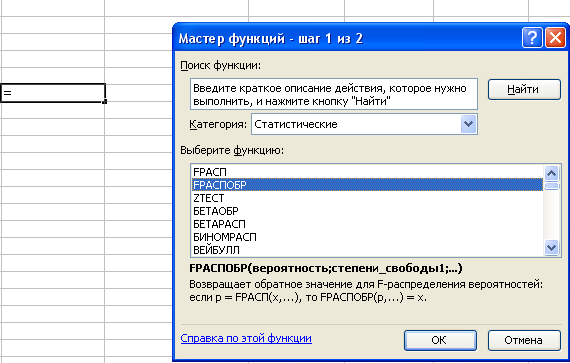
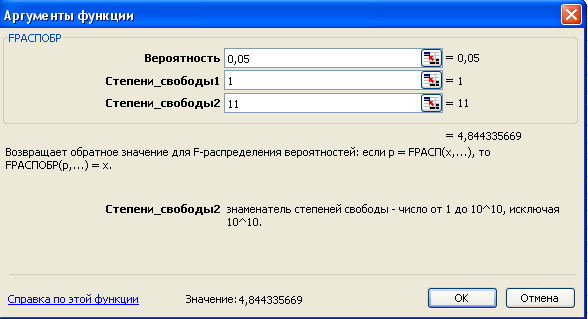
Поскольку расчетное значение F-критерия больше табличного, равного 4,84, нулевая гипотеза об отсутствии значимой связи признаков x и y отклоняется и делается вывод о существенности этой связи.
4) Оценим статистическую значимость параметров a и b в уравнении регрессии с помощью t- критерия Стъюдента.
Расчетные значения
статистики Стъюдента
,
.
Соответствующее табличное значение
можно определить через статистическую
функцию СТЪЮДРАСПОБР,
число степеней свободы равно
.
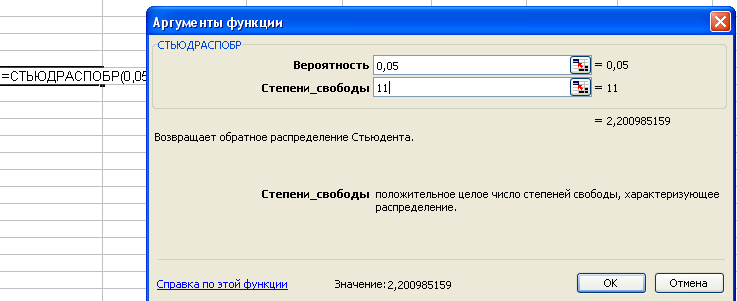
Поскольку фактические значения по абсолютной величине превышают табличное, равное 2,2, гипотезу о несущественности параметров регрессии можно отклонить.
5) Определим среднюю
ошибку аппроксимации,
.
Понадобится выполнение вспомогательных
расчетов, оформленных в виде таблицы.
|
|
x |
y |
|
|
|
|
8 |
5 |
5,440500341 |
31,99374573 |
|
|
5 |
10 |
5,143440944 |
2,868818882 |
|
|
4,9 |
12 |
5,024617185 |
2,543207862 |
|
|
4 |
15 |
4,846381547 |
21,15953867 |
|
|
3,8 |
20 |
4,54932215 |
19,71900394 |
|
|
3,5 |
22 |
4,430498391 |
26,58566831 |
|
|
3,8 |
25 |
4,252262752 |
11,90165138 |
|
|
3,7 |
30 |
3,955203355 |
6,897387976 |
|
|
3,6 |
35 |
3,658143958 |
1,615109941 |
|
|
3,5 |
36 |
3,598732078 |
2,820916526 |
|
|
3,4 |
40 |
3,361084561 |
1,144571747 |
|
|
3 |
50 |
2,766965766 |
7,767807796 |
|
|
3 |
60 |
2,172846972 |
27,57176761 |
|
Среднее |
4,092307692 |
27,69230769 |
|
12,66070741 |
Таким образом, средняя ошибка аппроксимации по данному уравнению регрессии составляет 12,66%, модель парной линейной регрессии можно признать удовлетворительной и пригодной для прогнозирования.
6) Выполним
количественную оценку влияния фактора
x
на фактор y,
используя коэффициент эластичности.
Для парной линейной регрессии его можно
найти по формуле
.
Имеем
.
Следовательно, при увеличении количества слушателей на 1% годовая цена уменьшится на 0,4%.
7) Выполним расчет прогноза y при увеличении фактора x на 25% от среднего.
Прогнозное значение
.
Точечный прогноз
признака y:
.
Средняя ошибка
прогноза равна
,
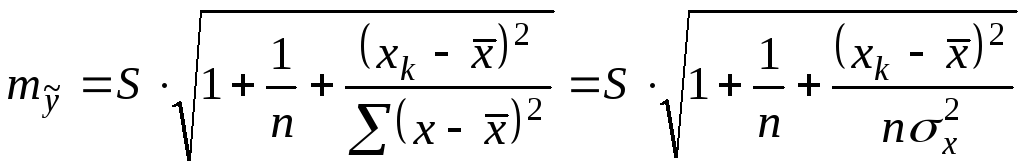где
–
остаточная дисперсия,
–дисперсия фактора x.
Численное значение
суммы
в протоколе обозначено как остаточное
SS.
Тогда
,
.
Самый быстрый
способ получения вспомогательных
характеристик
– среднего значения фактора x
и
-
дисперсии, воспользоваться инструментом
Описательная
статистика
в пакете Анализ
данных.
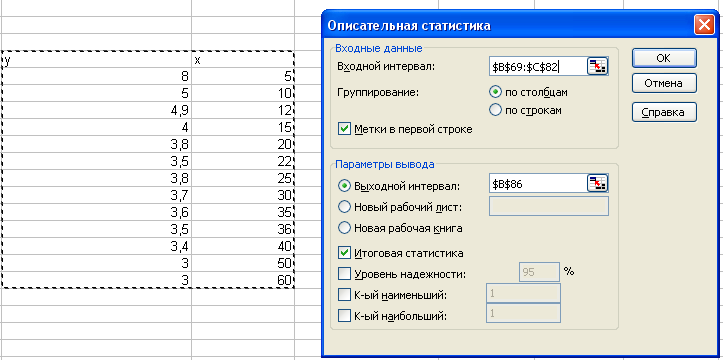
Протокол вывода результатов имеет вид
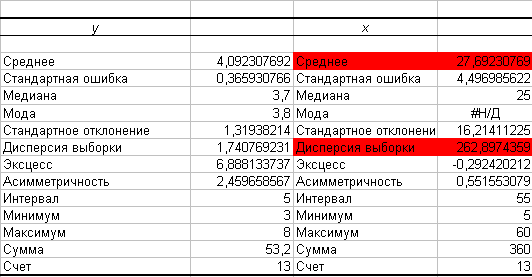
Имеем
.
Тогда
.
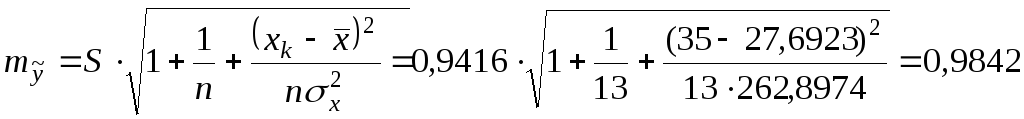Доверительный
интервал прогноза:
,
где
– соответствующее табличное значение
критерия Стъюдента (найдено ранее по
функции СТЪЮДРАСПОБР,
).
Следовательно,
;
,
т.е. можно быть уверенным на 95%, что цена годового курса при 35 слушателях будет варьироваться в указанных пределах (при точечном прогнозе цены в 3,65825 тыс. долл.).
8) Для построения диаграммы выполним следующие действия:
Шаг 1 Вставка/ Диаграмма/График
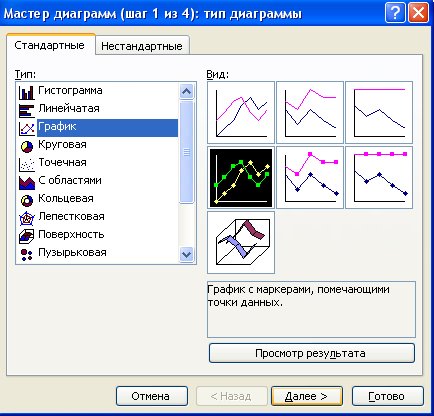
Шаг 2 Далее/Диапазон/Выделить столбец исходных значений фактора y
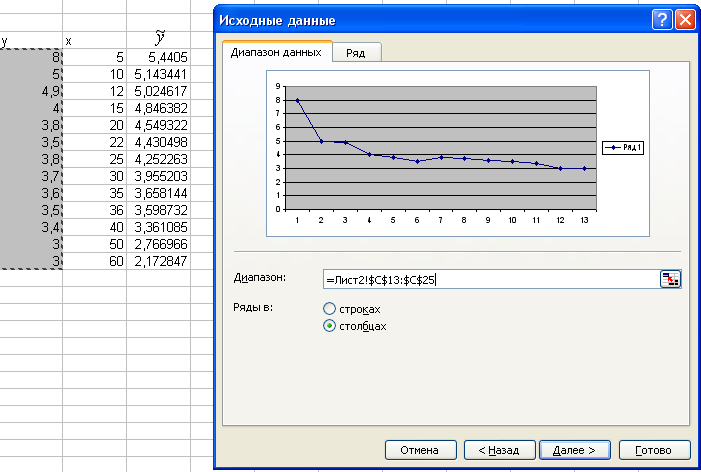
Шаг 3
Ряд/Добавить/Значения/Выделить
столбец регрессионных значений фактора
–
.
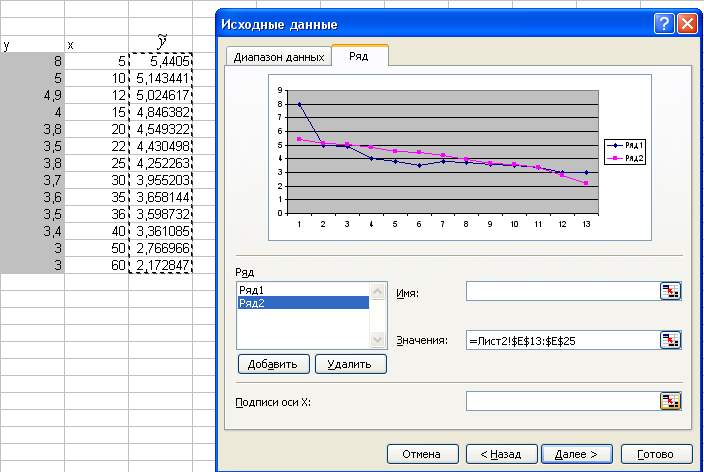
Шаг 4 Подписи оси X/Выделить столбец значений x.
Шаг 4 Каждому из рядов присвоить имя, подписать оси координат и название диаграммы.
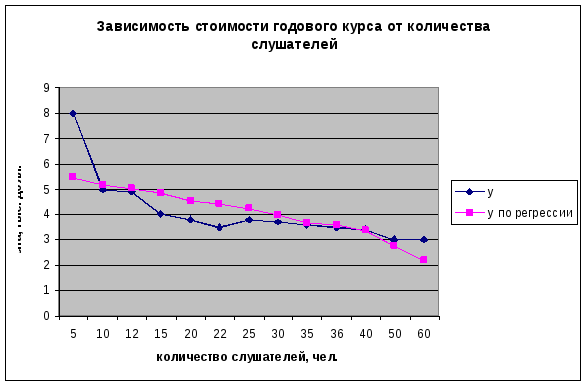
Примечание.
Для построения диаграммы значения фактора x должны быть отсортированы по возрастанию с сохранением соответствующего значения y. Это может быть сделано так Данные/Сортировка/Выделить столбец, в котором необходимо сделать сортировку. Например,
Задания для самостоятельной работы
Вариант 1
x– энерговооруженность на 10-ти предприятиях, кВт;
y– производительность труда, тыс. руб.
|
x |
2,8 |
2,2 |
3 |
3,5 |
3,2 |
3,7 |
4 |
4,8 |
6 |
5,4 |
|
y |
6,7 |
6,9 |
7,2 |
7,3 |
8,4 |
8,8 |
9,1 |
9,8 |
10,6 |
10,7 |
Вариант 2
x– энерговооруженность на 10-ти предприятиях, кВт;
y– производительность труда, тыс. руб.
|
x |
3,2 |
3,7 |
4 |
4,8 |
6 |
5,4 |
5,2 |
5,4 |
6 |
9 |
|
y |
8,4 |
8,8 |
9,1 |
9,8 |
10,6 |
10,7 |
11,1 |
11,8 |
12,1 |
12,4 |
Вариант 3
x– качество земли, баллы;
y– урожайность, ц/га.
|
x |
32 |
33 |
35 |
37 |
38 |
39 |
40 |
41 |
42 |
44 |
|
y |
19,5 |
19 |
20,5 |
21 |
20,8 |
21,4 |
23 |
23,3 |
24 |
24,5 |
Вариант 4
x– качество земли, баллы;
y– урожайность, ц/га.
|
x |
45 |
46 |
47 |
49 |
50 |
52 |
54 |
55 |
58 |
60 |
|
y |
24,2 |
25 |
27 |
26,8 |
27,2 |
28 |
30 |
30,2 |
32 |
33 |
Вариант 5
x– товарооборот;
y–издержки обращения по отношению к товарообороту.
|
x |
7 |
10 |
15 |
20 |
30 |
45 |
60 |
120 |
|
y |
10 |
9 |
7,5 |
6 |
6,3 |
5,8 |
5,4 |
5 |
Вариант 6
x– электровооруженность на одного рабочего;
y– выпуск готовой продукции на одного рабочего.
|
x |
2 |
5 |
3 |
7 |
2 |
6 |
4 |
9 |
8 |
4 |
|
y |
3 |
6 |
4 |
6 |
4 |
8 |
6 |
9 |
9 |
5 |