36.Основы теории погрешности. Прямая и обратная задача теории погрешности. Оценка погрешности. Понятие погрешности.

Погрешность – разница между точным значением величины и известным значением величины. Абсолютная погрешность – модуль этой разности. Известное значение называют приближённым. Погрешность возникает в случае неправильных исходных данных, в результате округления или упрощения математической задачи. Погрешность принято делить на три вида:

1. Неустранимая погрешность. Возникает из-за неточных исходных данных независимо от используемых методов и способов вычисления.

2. Погрешность метода – возникает из-за приближённого характера численных методов, которые используются при вычислениях (например, и ).

3. Вычислительная погрешность – это погрешность, связанная с ограниченным количеством разрядов ЭВМ.

Вычислительная ошибка всегда связанна с процедурой округления и само округление – попытка уменьшить вычислительную погрешность. Основная задача теории погрешности – оценить получаемую погрешность и предложить методы её уменьшения. Общая погрешность является суммой всех трёх видов погрешностей.

Опр 1. Абсолютной погрешностью приближенной величины называется модуль разности приближённого и точного значения величины:

Опр 2. Относительной погрешностью называется отношение абсолютной погрешности к модулю приближённой величины:

Абсолютную погрешность практически невозможно определить, т.к. не известно точное значение. Поэтому пользуются оценками величины.

По определению обе погрешности положительны, а относительная погрешность .

Оценка погрешности.

По определению дано, что абсолютную погрешность найти никогда точно нельзя. Пользуются её оценками.

Опр 3. Оценка погрешности называют положительную величину , которая заблаговременно больше либо равна :

По данному определению понятно что оценок бесконечно много.Среди всех возможных оценок есть наименьшая. Такая оценка называется предельной погрешностью. В некоторых случаях предельная погрешность равна абсолютной, а может быть и большей. Как правило, при вычислениях пользуются оценками погрешности не зная самой погрешности. Поэтому используют абсолютную погрешность.

Если известна абсолютная погрешность или какая-то её оценка, то можно утверждать что точное значение принадлежит отрезку:

Данный отрезок принято называть интервалом неопределённости. Точное значение где-то в этом отрезке. Для удобства его обозначают . Если число задано с погрешностью, то его цифры делятся на верные и приближённые. Все цифры, кот. по разряду больше погрешности назыв. верными, а остальные приближенными.Принято в абсолютной погрешности оставлять не более двух значащих цифр записи чисел записывают только одну приближённую цифру. В приближённом выражении производят округления таким образом, что бы приближённых цифр тоже осталось не более двух.

Существует также косвенная оценка погрешности – при итерационных вычислениях результатом является последовательность, которая сходится к искомому значению. Для оценки погрешности между пределом последовательности и очередным элементом пользуются такой оценкой:

Прямая и обратная задача теории погрешности.

Основной проблемой теории погрешности является поиск оценок. Выделяют прямую и обратную задачи теории погрешности.

1. Прямая задача: заданы приближённые величины А, B, C, D… и их абсолютные погрешности и функция . Требуется построить оценку погрешности функции . Для решения прямой задачи используется определение или метод разложения в ряд. Рассмотрим вариант определения.

А) Пусть дано, , ; требуется найти .

.

=

С помощью определений абсолютной и относительной погрешности можно построить таблицу погрешностей при математических вычислениях.

Абсолютная погрешность суммы равна сумме погрешностей.

Для произведения : =

Для разности:

Следовательно, если производить вычитание близких величин, относительная погрешность может значительно возрастать.

Формула для оценки погрешности отношения :

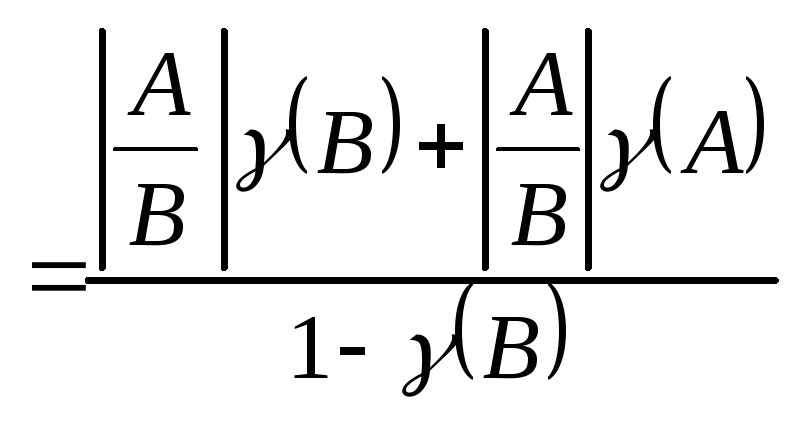
Б) Оценивание погрешности разложением в ряд Тейлора.

Так как данная оценка бесконечна, то пользуются последовательными приближениями. В первом приближении 1 –й элемент ряда:

во втором соответственно второй - в третьем – d(A)=dF₂+.

Формула для n - го приближения:

Очевидно, что нужно вычислять приближения последовательно, сначала вычислив 1-ое, проверить достаточно ли точна погрешность, затем второе и т.д.

Для функций двух аргументов F(A,B) разложение будет гораздо, сложнее:

dF≤(/sF/sA/)*d(A)+(/sF/sB/)*d(B)+(/s²F/sAsB/)*d²(A)+(/s²F/sB²/)*d²(B), где s – частная производная

На практике (для таких функций) ограничиваются первым приближением.

Обратная задача: Заданы приближенные значения A,B,C,D,…; F(A,B,C,D,…); d(F)≤ε Найти при каких значениях d(А), d(B), d(C), d(D) достигается заданная погрешность функции. Для решения обратной задачи нужны дополнительные условия на погрешности, иначе задача имеет много решений. Если же наложить условия оптимальности то задача сводится к условной либо безусловной оптимизации. Существует несколько вариантов упрощённых величин:

А) Вариант равных вкладов. Предполагается, что в первом приближении каждая величина даёт равный вклад:

Пусть всего величин K. Значит и (M – первое приближение).

Б) Метод равных погрешностей.

В) Задача условной оптимизации.

Если использовать первое приближение и искать его минимум (min d₁(F)) при различных значениях погрешности, то получится задача линейного программирования; если будем использовать второе и более высокие приближения, то нужно использовать задачу нелинейного программирования. На практике используют вариант равных вкладов и равных погрешностей на задаче линейного программирования.